數(shù)學“三勢能”讓思維轉(zhuǎn)換更自然*
●
(蕭山區(qū)第六高級中學,浙江 杭州 311261)
1 緣起
匈牙利數(shù)學家路莎·彼得所說:“數(shù)學家們解題往往不是對問題進行正面攻擊,而是將它不斷變形,而是把它們變?yōu)槟軌虻玫浇鉀Q的問題.”我們在學習過程中,經(jīng)常會碰到不同的教學思路、不同的解題方法、不同的視角去解決同一個問題.不同的視角之間的思維轉(zhuǎn)換如何才能實現(xiàn)?怎樣才能更加自然?如何提高學生思維轉(zhuǎn)換的主動性?這些都是我們值得研究的課題.
2 操作與實踐
勢能是儲存于一個系統(tǒng)內(nèi)的能量,也可以釋放或者轉(zhuǎn)化為其他形式的能量.雖然這是一個物理學上的概念,但數(shù)學本身就是一個龐大、復雜的系統(tǒng),因此我們可以認為數(shù)學內(nèi)部具有巨大的勢能,通過一定方式將其能量釋放出來就能為數(shù)學的發(fā)展做出貢獻.高中數(shù)學也可以充分利用此類“勢能”進行思維轉(zhuǎn)換,筆者根據(jù)自己的實踐把它分為順勢、造勢、蓄勢.
2.1 思維轉(zhuǎn)換之順勢轉(zhuǎn)換
任何新事物產(chǎn)生之前,必定會有一些萌芽.解題也是如此,首先要分析條件與目標,仔細閱讀題目的各個主要部分,依次對它們進行考慮.目標的內(nèi)容是什么,會涉及哪些相關(guān)知識與方法;條件與目標呈現(xiàn)的是怎樣的一種數(shù)學結(jié)構(gòu),與已經(jīng)學過的知識是否存在直接的聯(lián)系或類似性.這些都是題目中所蘊含的勢能,我們要順著這些勢能實現(xiàn)思維轉(zhuǎn)換.
因此所謂順勢就是通過目標指引、結(jié)構(gòu)分析等手段把問題化歸到學生所熟悉的知識或方法,也就是接近學生的最近發(fā)展區(qū).據(jù)此筆者把它分為順目標之勢與順結(jié)構(gòu)之勢.
1)順目標之勢.
目標原則是思維轉(zhuǎn)換的基本原則之一,其作用就是指引.方向可以是條件到結(jié)論,也可以從結(jié)論到條件,本質(zhì)就是已知與未知的互化.
案例1解三角形一例.
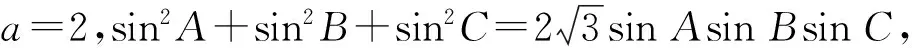
轉(zhuǎn)化1將條件轉(zhuǎn)化為
但與利用余弦定理求cosA有差異.
轉(zhuǎn)化2不放棄,將余弦定理代入式(1)化簡得
(2)
此式形式已達最簡,但離目標sinA或cosA較遠.
此時有學生提出由式(1)和式(2)結(jié)合余弦定理與平方關(guān)系聯(lián)立可以解出b,c,sinA,cosA.想法不錯,充分利用了方程的思想,但耗時耗力.
轉(zhuǎn)化3此時需要另辟蹊徑,回頭檢查并沒發(fā)現(xiàn)問題,觀察式(2)得
即
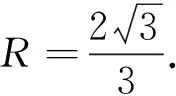
點評此題實際上是以前解三角形問題中求周長最值(或面積)問題的延伸.如已知△ABC中,a,b,c分別是內(nèi)角A,B,C的對邊,A=60°,a=2,求周長(或b+c)的最大值.利用余弦定理結(jié)合基本不等式可解決.
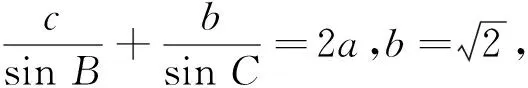
反思此題結(jié)構(gòu)簡單卻不能直接到達目標,雖說聯(lián)立方程可行卻難以操作,此時題目的難點就像爬山即將到達山頂一樣,只要一陣涼風吹來并想想目標所在即可順勢而下突破難點.
2)順結(jié)構(gòu)之勢.
著名的布爾巴基學派的基本指導思想就是結(jié)構(gòu)主義,他們認為全部數(shù)學基于3種結(jié)構(gòu):代數(shù)結(jié)構(gòu)、序結(jié)構(gòu)和拓撲結(jié)構(gòu).高中數(shù)學學習,特別是思維的轉(zhuǎn)換自然離不開對結(jié)構(gòu)的分析.無論是實際問題或情景的結(jié)構(gòu),還是抽象的數(shù)學問題的結(jié)構(gòu),要實現(xiàn)條件與目標的相互轉(zhuǎn)換都需分析其本質(zhì)結(jié)構(gòu).可按識別結(jié)構(gòu)、再進行聯(lián)想結(jié)構(gòu)、轉(zhuǎn)換結(jié)構(gòu)的步驟進行.
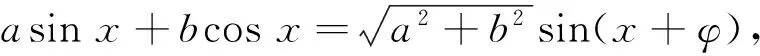
案例2函數(shù)單調(diào)性定義運用.
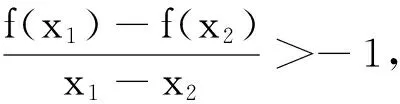
A.(-∞,0) B.(-∞,1)
C.(-1,0)∪(0,3) D.(-∞,0)∪(0,1)
此題乍一看無從下手,聯(lián)想單調(diào)性定義就可以依據(jù)其結(jié)構(gòu)進行逐步轉(zhuǎn)化.
條件轉(zhuǎn)化1)聯(lián)想函數(shù)單調(diào)性定義:變形為
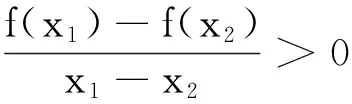
2)聯(lián)想分式不等式解法:函數(shù)g(x)=f(x)+x在R上單調(diào)遞增.
目標轉(zhuǎn)化結(jié)構(gòu)轉(zhuǎn)換1:換元,令t=log2|3x-1|,則不等式可化為f(t)<2-t;
結(jié)構(gòu)轉(zhuǎn)換2:變形,再化為g(t) 結(jié)構(gòu)轉(zhuǎn)換3:求解,由條件轉(zhuǎn)換2可知t<1,即log2|3x-1|<1,求得x<1. 點評單調(diào)性定義常考常變,因此有必要對定義的結(jié)構(gòu)進行適當變形以加深概念的理解運用和知識模塊之間的相互聯(lián)系. 反思抓住數(shù)學概念的代數(shù)結(jié)構(gòu)或幾何結(jié)構(gòu)有助于認識數(shù)學概念的本質(zhì),從而把繁難問題簡單化、陌生問題熟悉化. 數(shù)學上的概念、方法是歷史上經(jīng)歷了多年的沉積才形成的,如果直接把它放到學生面前,學生對它是陌生的,就算勉強接受也是被動的,不具有深刻性和持續(xù)性.很多數(shù)學知識高高在上,處在高位運行態(tài)勢,勢能強大卻無法落地.我們有必要對概念的形成、定理的推導、方法的產(chǎn)生進行適當鋪墊,營造思維轉(zhuǎn)換的氛圍. 因此筆者認為造勢就是通過數(shù)學史融入教學、挖掘?qū)W生的最近發(fā)展區(qū)、采用多媒體或網(wǎng)絡(luò)技術(shù)等多種方式讓知識從高位勢能轉(zhuǎn)換為低位勢能,從而實現(xiàn)思維的自然轉(zhuǎn)換. 在教學中經(jīng)常會遇到突兀性問題,如兩角差的余弦公式,由三角函數(shù)線方法突然轉(zhuǎn)到向量方法讓人恍惚.針對這一轉(zhuǎn)換可進行適當?shù)脑靹菀詫崿F(xiàn)思維的自然轉(zhuǎn)換.譬如:1)從教材的分布來講,為什么第一章“三角函數(shù)”與第三章“三角恒等變換”之間會插入第二章“平面向量”,這不就是在誘導我們使用向量方法來解決三角問題嗎?2)從已產(chǎn)生的公式結(jié)構(gòu)來看,cosαcosβ+sinαsinβ就是x1x2+y1y2,即數(shù)量積的坐標形式.如此造勢即可完成三角方法與向量方法之間的自然轉(zhuǎn)換,此類問題在方法教學與解題教學中經(jīng)常出現(xiàn),下面再以錯位相減法為例說明造勢轉(zhuǎn)換. 案例3錯位相減法. 錯位相減法是數(shù)列求和中的常用方法之一,但面對通項是等差乘等比的情形,很多學生到高三仍舊想不到此方法,這是為何? 回看教材的推導過程 Sn=a1+a1q+a1q2+…+a1qn-1,(3) 我們發(fā)現(xiàn),如果用公比q乘以式(3)的兩邊,可得 qSn=a1q+a1q2+…+a1qn-1+a1qn,(4) 兩式相減可得…… 就此我們發(fā)現(xiàn)“用公比q乘式(3)的兩邊”這一步來得太過突然,這樣雖然解決了等比求和公式的推導問題,但學生思維的轉(zhuǎn)換還是存在障礙的,因此有必要對思維轉(zhuǎn)換進行造勢.下面是筆者總結(jié)的兩種造勢方式. 造勢1依方法造勢[1]. 師:常見的求和方法有哪些? 生:倒序相加、裂項相消、錯位相減等. 師:倒序相加法用來求什么數(shù)列的和? 生:等差數(shù)列. 師:能具體描述一下嗎? 生:式(3)倒過來寫Sn=an+an-1+…+a1.結(jié)合性質(zhì)a1+an=a2+an-1=…,可得等差數(shù)列求和公式. 師:倒序相加的目的是什么? 生:減少項數(shù)得到一個簡潔的公式. 師:我們再看裂項相消法,能舉一個例子說明嗎?怎么解答? 師:由此看出裂項的目的是什么? 生:相消即減少了項數(shù). 師:兩種求和方法的共同目的是什么? 生:減少項數(shù). 師:能再舉一個例子嗎? 師:錯位相減法中“用公比q乘式(3)的兩邊”這一步目的是什么? 生:減少項數(shù). 由此錯位相減法才真正引入了…… 造勢2依目標造勢. 師:類比等比數(shù)列的通項公式an=a1qn-1,前n項和Sn應該用什么量表示? 生:首項和公比. 師:通項代入后 Sn=a1+a1q+a1q2+…+a1qn-1, 怎樣減少項數(shù)?等比數(shù)列中你還有什么知識可用? 生:利用等比數(shù)列定義,每一項乘公比變成后一項. 師:后面各項提出q后變成怎樣一個式子? 生:Sn=a1+q(a1+aq+…+a1qn-2),即Sn-qSn=a1-a1qn-1. 師:這不就是錯位相減法的框架嗎?我們將其變形為錯位相減法: Sn=a1+a2+…+an, qSn=a2+…+anq, 兩式相減得 (1-q)Sn=a1-a1qn-1, …… 點評兩種造勢方式各有側(cè)重,造勢1側(cè)重如何引入和式兩邊同乘公比這一方法,造勢2側(cè)重目標的構(gòu)成研究. 理解數(shù)學概念、方法產(chǎn)生的歷程,把數(shù)學知識的學術(shù)形態(tài)轉(zhuǎn)化成教育形態(tài)是數(shù)學教學基本目標之一.雖然我們并不是很清楚高斯是如何得到錯位相減這種求和方法的,但我們通過造勢使學生的思維轉(zhuǎn)換順利實現(xiàn),這就達成了教學的目標. 文獻[2]中提到了10種轉(zhuǎn)換機制,如:正面問題反面化、整體問題局部化、運動問題靜止化等等.要讓學生形成這些轉(zhuǎn)換機制,日常教學中教師不僅要重視基礎(chǔ)知識、基本技能的鞏固,也要重視基本思想方法、基本數(shù)學活動經(jīng)驗的積累,這就是我們經(jīng)常強調(diào)的四基.只有當四基的儲備到達一定層次,就像水庫蓄水到一定水位水流才能傾瀉而出,學生的思維之花才能綻放,筆者稱之為蓄勢. 蓄勢首要當然是雙基的積累,不再贅述.這里筆者著重提出處理數(shù)學問題的方法與策略的積累. 2.3.1 蓄方法之勢 數(shù)學的解題方法很多,對不同的問題有不同的方法.如求函數(shù)的值域問題:二次函數(shù)可用配方法、數(shù)形結(jié)合法;一次分式型函數(shù)可用分離常數(shù)法、反函數(shù)法;高次函數(shù)可用導數(shù)法等等.有時對同一個問題有不同視角的多種解法,如下面這個解析幾何題,筆者就采用了解析法、向量法、幾何法等多種方法.方法的積累我們姑且稱之為蓄方法之勢. 1)求直線AP斜率的取值范圍; 2)求|PA|·|PQ|的最大值. (2017年浙江省數(shù)學高考試題第21題) 方法1解析法 1)設(shè)點P(x,y),易得直線AP的斜率k∈(-1,1). 2)聯(lián)立直線AP與BQ的方程解出點Q,再進一步求得 |PA|·|PQ|=(1-k)(k+1)3. 令f(k)=(1-k)(k+1)3,其中k∈(-1,1),則 此法運算量超大,人稱“暴力解法”,主要表現(xiàn)為3步:一是求點Q坐標,二是用弦長公式計算|PA|·|PQ|,三是導數(shù)法求最值.每一步的運算量都不小,雖說解決解析幾何問題必須有扎實的運算功底,但作為核心素養(yǎng)的數(shù)學運算,首先要研究清楚算法,選擇適當?shù)乃惴ㄊ潜匾模虼擞斜匾獡Q一個視角處理長度之積,即進行思維轉(zhuǎn)換. 方法2向量法 向量轉(zhuǎn)換2考慮到AP⊥BQ,運用向量運算或投影法可將|PA|·|PQ|進一步轉(zhuǎn)換為 方法3幾何法 圓冪轉(zhuǎn)換由AP⊥BQ聯(lián)想到圓,點Q在以AB為直徑的圓上,由圓冪定理可知 以下同方法1和方法2. 點評3種方法實現(xiàn)了幾何問題解析化再到幾何法的多次轉(zhuǎn)換,可見命題人立意之深.高考中解析幾何題的正確解答,可以實現(xiàn)從中等得分到高分的跨越,此題不僅考查了解析幾何知識,還必須使用導數(shù)知識才能解決最值問題,方法1將耗費學生大量時間,因此需要平時積累方法對思維進行轉(zhuǎn)換,由此可見蓄勢的重要性. 反思高考試題是講究區(qū)分度的,要想在難度系數(shù)比較高的題目中拿到分數(shù),不僅要掌握高中數(shù)學的四基,也要掌握常見的思維轉(zhuǎn)換方式,如代數(shù)與幾何的互化、高維問題低維化、一般問題特殊化等等.在經(jīng)歷一定程度的訓練后才能實現(xiàn)熟能生巧,因此三勢中蓄勢才是最重要的. 2.3.2 蓄策略之勢 以上我們提到蓄方法之勢,對解題方法的使用其實還只是程序性知識.對一些重要的知識模塊中的常見問題或常見題型,必須對其進行適當拓展和提升,使其上升為能夠讓學生接受的策略性知識,稱之為蓄策略之勢.下面以數(shù)列前n項和的最值問題為例加以說明. 案例5等差數(shù)列的前n項和的最值問題. 已知等差數(shù)列{an},a1=26,a2=22,則其前n項和Sn何時取得最大值? 本題可采用單調(diào)性法和二次函數(shù)法解決(略).對于一般的等差數(shù)列{an},我們均可以采用以上兩種方法加以解決,再升級后還可成為其他數(shù)列求最值的方法. 方法1(符號法)由首項及通項的符號確定Sn的最值. 方法2(函數(shù)法)利用Sn是n的函數(shù),利用函數(shù)知識求最值. 求解最值. 點評從一個題目的解決,推廣到一類問題的解決,再上升到策略性知識,這讓學生的思維不僅深刻而且廣闊. 反思學生不僅要會解一個題目,而且要能夠推廣到一般情形.在推廣過程中也會發(fā)現(xiàn),并不是每種方法都適用任何情形或題目,因此在解題過程中我們會選擇適當?shù)牟呗?以把控解題的方向避免無謂的損失.策略的選擇需要日常的學習經(jīng)驗的積累,即蓄策略之勢. 通過近幾年的實踐,我們發(fā)現(xiàn)數(shù)學“三勢能”對學生的思維轉(zhuǎn)換的主動性、靈活性、縝密性等起到了非常重要的作用[3].順勢、造勢實現(xiàn)了勢能從高位到低位的轉(zhuǎn)換,而蓄勢實現(xiàn)了低位到高位的轉(zhuǎn)換.總之,數(shù)學三勢能有助于實現(xiàn)思維的自然轉(zhuǎn)換,對數(shù)學學習的效率提升大有作用,值得大家去進一步研究. [1] 李湘.順應學生思維 促進學生發(fā)展[J].中學數(shù)學月刊,2017(5):21-24. [2] 李發(fā)武,李良貴.引入轉(zhuǎn)換機制解題[J].數(shù)學通報,2001(4):26-28. [3] 周曉.高中數(shù)學教學要培養(yǎng)學生轉(zhuǎn)換思維的能力[J].考試周刊,2015(79):73-74.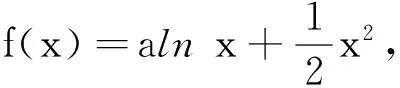
2.2 思維轉(zhuǎn)換之造勢轉(zhuǎn)換
2.3 思維轉(zhuǎn)換之蓄勢轉(zhuǎn)換
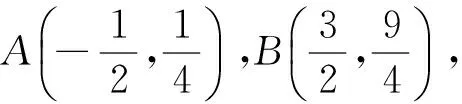
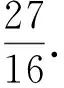
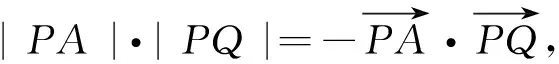
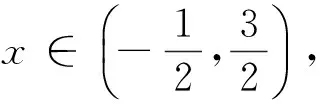
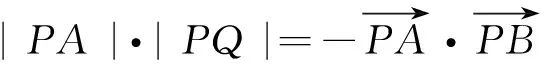
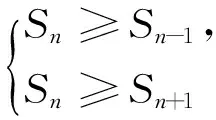
3 結(jié)束語

