高中數學核心素養的培養*
——以“從同心圓到同心圓錐曲線”為例

●

(北京師范大學貴陽附屬中學,貴州 貴陽 550081)

●胡典順

(華中師范大學數學與統計學學院,湖北 武漢 430079)

近年來，“核心素養”已經成為教育界的重要議題，而且引領了課程教材改革以及教學方式改革等等.數學核心素養的本質，是描述一個人經過數學教育后應當具有的數學特質，大體上可分為“三會”，即：會用數學的眼光觀察世界，會用數學的思維思考世界，會用數學的語言表達世界[1].那如何培養高中生的數學核心素養呢？筆者以“從同心圓到同心圓錐曲線”為例，談談數學抽象、直觀想象、數學建模、邏輯推理和數學運算等核心素養的培養.

1 類比同心圓的概念，抽象出同心圓錐曲線的概念，培養數學抽象素養

同心圓是兩個圓心重合而半徑不等的圓，它有很多典型的性質和優美的結論.類比到圓錐曲線，如果兩條圓錐曲線有著公共的焦點F，且與F對應的準線f也是公共的，那么這樣的圓錐曲線與同心圓是否具有相似的性質呢？首先，我們類比同心圓的概念，給出這類圓錐曲線的概念.

定義設兩條圓錐曲線有著公共的焦點F，且與F對應的準線f也是公共的，則稱這兩條圓錐曲線為同心圓錐曲線.

設橢圓和拋物線有著公共的焦點F，且與F對應的準線f也是公共的，則稱這樣的橢圓和拋物線為同心圓錐曲線.

2 類比同心圓的性質，驗證同心圓錐曲線的性質，培養直觀想象素養

本文討論的是橢圓和拋物線為同心圓錐曲線的情形.通過類比同心圓的性質，然后借助超級畫板進行驗證，從而得到同心圓錐曲線的優美性質.

圖1

命題1如圖1，設⊙Γ1和⊙Γ2是同心圓，公共圓心為O,過⊙Γ2上一點A作⊙Γ1的兩條切線，切點為M,N，那么

1) ∠MON為定值；

2)OA平分∠MON.

上述兩個結論類比到同心圓錐曲線，可得到：

命題2如圖2，設橢圓和拋物線為同心圓錐曲線，F和f分別為它們的公共焦點和對應的公共準線，過拋物線上一點A作橢圓的兩條切線，切點為M,N，那么

1)FA平分∠MFN；

2)∠MFN為定值.

圖2 圖3

利用超級畫板驗證，如圖3.

通過超級畫板探究發現：當點A在拋物線上運動時，∠MFN的大小始終沒有變，為一個定值，而且∠AFM=∠AFN.

3 建立直角坐標系，合理選擇標準方程，培養數學建模素養

建立平面直角坐標系.如果設拋物線方程為標準方程，那么可得到橢圓的焦點和準線，但這時橢圓不是標準方程，此時已知它的焦點和準線，如何求出它的標準方程呢？筆者做了嘗試，發現不易求出橢圓的標準方程，因此應該設橢圓方程為標準方程.

圖4

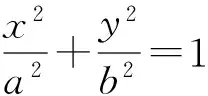
化簡得

即

消去x，得

消去y，得

4 分析問題，探尋問題解決的策略，培養邏輯推理素養

如何證明FA平分∠MFN呢？有兩種解決方案:

方案1證明∠AFN=∠AFM,考慮向量的夾角公式，得

∠AFN=∠AFM?cos∠AFN=cos∠AFM?

方案2證明射線FA上的點到∠MFN兩邊的距離相等.可取這一點為A(x0,y0)，直線FM的方程為

即

y1x-(x1+c)y+c(x1+y1)+c2=0.

同理可得,直線FN的方程為

y2x-(x2+c)y+c(x2+y2)+c2=0,

從而

∠AFN=∠AFM，

此時，遇到了與方案1同樣的困難,即很難證明上式成立，這說明這兩種方案在理論上行得通，但在實際操作中難以實施，遇到了數學運算上的困難.那如何繞過這個困難，找到解決問題的方案呢？

著名數學教育家波利亞告訴我們：解題需要找出已知數據與未知數據之間的聯系.如果找不到直接的聯系，就不得不考慮輔助題目.思考：你能找到一道與命題2有關的題目嗎？這里有一道題目和命題2有關而且以前做過，你能利用它嗎？

A.外心 B.內心 C.重心 D.垂心

(2003年全國數學高考新課程卷第4題)

5 合理選擇運算方法，培養數學運算素養

數學運算素養包括理解運算對象、探究運算方向、選擇運算方法、設計運算程序、求得運算結果等等.對于命題2而言，合理選擇運算方法最為重要，選對了運算方法，就可以簡化運算，縮短解題的長度，提高解題的效率.

下面證明式(1)成立:

將式(2)和式(3)代入式(1)，得式(1)等價于

即

上式顯然成立，因此式(1)成立，故FA平分∠MFN.

2)要證明∠MFN為定值，需要將它用坐標來表示，因此選用夾角公式求cos∠MFN的值比較合理，即

其中e為橢圓的離心率.下面證明式(4)是定值:

x1x2+c(x1+x2)+y1y2+c2=

將式(5)和式(6)代入式(4)，得

故∠MFN為定值.

6 結束語

數學核心素養與數學基本思想、數學思想方法等密切相關[2].數學核心素養是數學基本思想在學習某一個或幾個領域內容中的具體表現.數學思想方法則是體現如何從操作層面上實現數學核心素養和體現數學基本思想方法.數學核心素養對于理解數學學科的本質、設計數學教學以及開展數學評價等有著重要的意義和價值[3].

對于高中數學核心素養，應該建立起核心素養與數學教學內容的關聯，創設合適的數學情景，提出合適的數學問題，啟發學生獨立思考，使學生在掌握數學技能的同時，感受數學本質，從而積累數學思維和實踐經驗，形成和發展數學核心素養.

[1] 馬云鵬.關于數學核心素養的幾個問題[J].課程·教材·教法，2015,35(9)：36-39.

[2] 陳玉娟.例談高中數學核心素養的培養——從課堂教學中數學運算的維度[J].數學通報，2016(8)：34-36.

[3] 張嵐.基于數學核心素養的解析幾何教學——談數學運算能力的提升[J].中學教研(數學)，2017(5)：27-30.