幾何畫(huà)板是數(shù)學(xué)發(fā)現(xiàn)的望遠(yuǎn)鏡*
——對(duì)觀摩研討課一道例題的課后探索

●

(明港中學(xué)，浙江 寧波 315806)

最近，筆者參加了一次同課異構(gòu)的觀摩研討課活動(dòng)，兩位教師都重點(diǎn)講了同一道課本例題：

例1已知內(nèi)接于圓的四邊形的對(duì)角線(xiàn)互相垂直，求證:圓心到一邊的距離等于這邊所對(duì)邊長(zhǎng)的一半.

圖1

兩位教師教態(tài)自然，著眼于培養(yǎng)學(xué)生的數(shù)學(xué)核心素養(yǎng)，對(duì)比講解笛卡爾的解析法和歐幾里得的幾何法，啟發(fā)學(xué)生積極回答和變式練習(xí).例1的教學(xué)片段是這兩節(jié)同課異構(gòu)的預(yù)設(shè)難點(diǎn)和實(shí)際亮點(diǎn)，贏得了聽(tīng)課教師的贊賞.

課后，我們對(duì)照兩位教師的教案，運(yùn)用幾何畫(huà)板動(dòng)態(tài)演示例1的示意圖，首先發(fā)現(xiàn)一個(gè)有關(guān)平行四邊形的新猜想：

猜想1在圖1的基礎(chǔ)上，取BC的中點(diǎn)F(如圖2所示)，則順次連接點(diǎn)O,F,H,E構(gòu)成平行四邊形.

圖2 圖3

復(fù)驗(yàn)以圖2中直線(xiàn)CA,DB分別為x軸、y軸，建立如圖3所示的直角坐標(biāo)系xHy.設(shè)點(diǎn)A(a,0),B(0,b),C(c,0),D(0,d)，則

從而

同理可得|OE|=|FH|.

要驗(yàn)證順次連接點(diǎn)O,F,H,E構(gòu)成平行四邊形，|OF|=|EH|且|OE|=|FH|是必要條件，還要考慮點(diǎn)O,F,H,E不共線(xiàn)的特殊情形和點(diǎn)O,H不重合的退化情形.

圖4 圖5

實(shí)際上，在已有的條件下，當(dāng)|HA|=|HD|≠|(zhì)HB|時(shí)，點(diǎn)O,F,H,E共線(xiàn)(如圖4所示)；當(dāng)|HA|=|HB|=|HC|=|HD|時(shí)，點(diǎn)O與點(diǎn)H重合(如圖5所示).總之，猜想1不正確.

猜想1雖然有差錯(cuò)，但復(fù)驗(yàn)過(guò)程所蘊(yùn)含的正確因素是極其寶貴的，從中能夠去偽存真地得到:

圖6

定理1如圖6，⊙O的內(nèi)接四邊形ABCD的兩條對(duì)角線(xiàn)互相垂直，垂足H不重合于圓心O.

1)取邊AD的中點(diǎn)E，取邊BC的中點(diǎn)F，則當(dāng)HA≠HD時(shí)，四邊形OFHE是平行四邊形；

2)取邊AB的中點(diǎn)M，取邊CD的中點(diǎn)N，則當(dāng)HA≠HB時(shí),四邊形ONHM是平行四邊形.

圓經(jīng)過(guò)壓縮變換就變成了橢圓，其中的兩條直線(xiàn)平行保持不變性，多點(diǎn)共線(xiàn)保持不變性，線(xiàn)段中點(diǎn)保持不變性，于是就容易頓悟到：

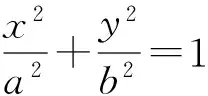
演示1運(yùn)用幾何畫(huà)板可檢驗(yàn)度量：

|OE|=|FH|, |OF|=|EH|,

|OM|=|NH|, |ON|=|MH|.

如圖7所示，符合結(jié)論.

圖7

演示2運(yùn)用幾何畫(huà)板，依次選點(diǎn)O,E通過(guò)變換窗口標(biāo)記向量，再把點(diǎn)F通過(guò)變換窗口按標(biāo)記向量平移，恰好重合于點(diǎn)H；依次選點(diǎn)O,M通過(guò)變換窗口標(biāo)記向量，再把點(diǎn)N通過(guò)變換窗口按標(biāo)記向量平移，恰好重合于點(diǎn)H.

證明依題意，設(shè)A(acosα,bsinα),B(acosβ,bsinβ),則H(acosβ,bsinα),C(-acosα,bsinα),D(acosβ,-bsinβ),可得

同理可證

kEH=kOF.

綜上所述，當(dāng)AD與BC不平行時(shí)，四邊形OFHE是平行四邊形；同理可證，當(dāng)AB與CD不平行時(shí)，四邊形ONHM是平行四邊形.

補(bǔ)充說(shuō)明1)在定理2的先決條件下，當(dāng)AD∥BC時(shí)，點(diǎn)O,F,H,E共線(xiàn)；當(dāng)AB∥CD時(shí)，點(diǎn)O,N,H,M共線(xiàn).

2)經(jīng)過(guò)幾何畫(huà)板的操作試驗(yàn)，假如將定理2中“兩條弦AC,BD分別垂直于y軸、x軸”推廣替換為“兩條弦AC,BD互相垂直”，如圖8所示，則相應(yīng)結(jié)論錯(cuò)誤.

圖8 圖9

3)經(jīng)過(guò)幾何畫(huà)板的操作試驗(yàn)，假如將定理2中“兩條弦AC,BD分別垂直于y軸、x軸，垂足H在橢圓內(nèi)”類(lèi)比替換為“兩條弦AC,BD所在直線(xiàn)分別垂直于y軸、x軸，垂足H在橢圓外”，如圖9所示，則相應(yīng)結(jié)論仍然正確.

4)回眸定理1中的圓，可作類(lèi)似于上述3)的幾何畫(huà)板操作試驗(yàn)(可用標(biāo)記向量進(jìn)行平移的快捷途徑)，也可得到相應(yīng)正確結(jié)論(示意圖略).

把定理3中的橢圓類(lèi)比到雙曲線(xiàn)中去思考，經(jīng)過(guò)幾何畫(huà)板演示(如圖10和圖11)后，可得到一個(gè)類(lèi)比結(jié)論：

圖10 圖11

從而

xE+xF=xH，

(1)

和yE+yF=yH.

(2)

事實(shí)上,

同理可得

yE+yF=yH.

于是，式(1)和式(2)成立，因此

提煉上述4個(gè)定理的共性，可以高度抽象出一個(gè)更加統(tǒng)一的大團(tuán)圓結(jié)論：

定理5如果有心二次曲線(xiàn)Ω(圓或橢圓或雙曲線(xiàn))的兩條弦AC,BD所在的直線(xiàn)分別垂直于該曲線(xiàn)Ω的兩條互相垂直的對(duì)稱(chēng)軸，直線(xiàn)AC與直線(xiàn)BD的垂足H不在該曲線(xiàn)Ω上，取弦AD,BC,AB,CD的中點(diǎn)依次為E,F,M,N，那么有向量等式

補(bǔ)充說(shuō)明在定理5中，假如直線(xiàn)AC與直線(xiàn)BD的垂足H在該曲線(xiàn)Ω上(前面的條件都不變)，那么弦AC和弦BD必然各有一個(gè)端點(diǎn)都重合于垂足H，不妨設(shè)點(diǎn)C和點(diǎn)B都重合于點(diǎn)H，那么“極限化的中點(diǎn)”F也重合于垂足H，而中點(diǎn)E重合于曲線(xiàn)Ω的中心，于是借用零向量也可以使該定理結(jié)論的4個(gè)向量等式仍然成立.

上面層層遞進(jìn)的一串探索流程，既有對(duì)教材內(nèi)涵的挖掘，又有對(duì)教法學(xué)法的指導(dǎo)，可以選作幾何畫(huà)板輔助探究性學(xué)習(xí)的課題設(shè)計(jì).

筆者余興未盡，最后談兩點(diǎn)啟示：

啟示1例1選自課本例題，平時(shí)我們對(duì)這道題熟視無(wú)睹，似乎沒(méi)有挖掘價(jià)值，其實(shí)不然.如果我們平時(shí)能像展示課的例題教學(xué)那樣對(duì)待課本的許多例習(xí)題，充分激活個(gè)體的創(chuàng)新潛質(zhì)，充分營(yíng)造群體的合作氛圍，把外界激勵(lì)自覺(jué)轉(zhuǎn)化為內(nèi)心驅(qū)動(dòng)，進(jìn)行匠心探索和細(xì)心品味，那么就可以發(fā)現(xiàn)許多數(shù)學(xué)新奧秘.

啟示2在把一道例題逐步抽象升華為5個(gè)定理的探索過(guò)程中，幾何畫(huà)板的動(dòng)態(tài)演示起到了不證先知的作用.美國(guó)數(shù)學(xué)史家克萊因說(shuō)過(guò)：“數(shù)學(xué)的最大進(jìn)步是由具有杰出的直覺(jué)能力的人所推動(dòng)的，而不是由具有構(gòu)造嚴(yán)格證明能力的人所推動(dòng)的”.現(xiàn)在看來(lái)，幾何畫(huà)板可以促使我們的數(shù)學(xué)直覺(jué)能力顯性化、快捷化，是我們一目了然地發(fā)現(xiàn)數(shù)學(xué)新奧秘的望遠(yuǎn)鏡.

[1] 陳咸存.用幾何畫(huà)板探究、猜想與驗(yàn)證[J].數(shù)學(xué)通報(bào)，2016(4)：26-28.

[2] 甘大旺.運(yùn)用幾何畫(huà)板畫(huà)圓錐曲線(xiàn)的三種方法[J].中學(xué)數(shù)學(xué)，2007(8)：23-26.