浮動滾子推桿等跨凸輪機構及其尺寸綜合的正-逆映射求交方法
范 武 林夢杰 李延平 常 勇,2
1.集美大學機械與能源工程學院,廈門,3610212.集美大學工程訓練中心,廈門,361021
0 引言
本文第四作者等[1]于2010年提出了浮動滾子推桿盤形凸輪機構Ⅰ類、Ⅱ類綜合問題及其準確描述,通過引入浮動數軸、瞬時/整程區(qū)間套等概念,得到了解存在性、存在特征的一整套解析公式,解決了浮動滾子推桿力鎖合盤形凸輪機構的第Ⅱ類尺寸綜合問題,之后,考慮到形鎖合機構綜合的復雜性和特殊性,于2012年引入往程/返程和向徑標刻線等概念,揭示了形鎖合機構在綜合路徑、方法步驟等方面的顯著差異,解決了浮動滾子推桿形鎖合盤形凸輪機構的第Ⅱ類尺寸綜合問題[2]。在文獻[1-2]研究成果的基礎上,又通過引入浮動坐標系、瞬時/整程選擇區(qū)域和最經濟搜索帶域等概念,采用離散降維快速求解方法,解決了浮動滾子推桿盤形凸輪機構的廣義第Ⅱ類尺寸綜合問題[3]。
與力鎖合凸輪機構[4-6]相比,形鎖合凸輪機構[7]具有運動精度高、抗沖擊能力強、壽命長和適用于高速等優(yōu)點,在內燃機、紡織、印刷、包裝和農業(yè)等領域應用廣泛[8-9]。探索與拓展形鎖合凸輪機構可能的構型空間并解決尺寸綜合問題[8-9],具有重要意義。
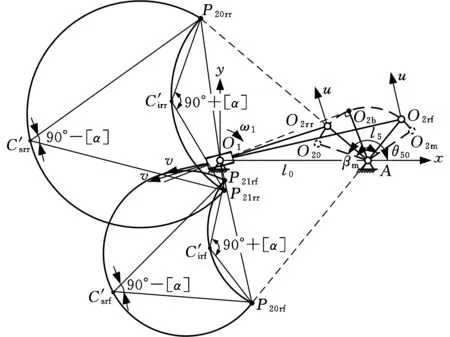
較之共軛、槽道凸輪機構,等徑凸輪機構求解困難,具有如下形態(tài)特征:主/副滾子中心C、C′和凸輪軸心O1三點共線,位于連桿方位線O1O2上。
能否跳脫和突破等徑凸輪機構“三點共線”傳統(tǒng)限定條件,提出形鎖合機構的新構型?若能,在尺寸綜合方面可否獲得正面收益?針對上述問題,筆者開展了相關研究,并由此提出了等跨凸輪機構的新構型。
1 等跨凸輪機構的形態(tài)特征及其尺寸綜合
問題的準確描述
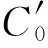
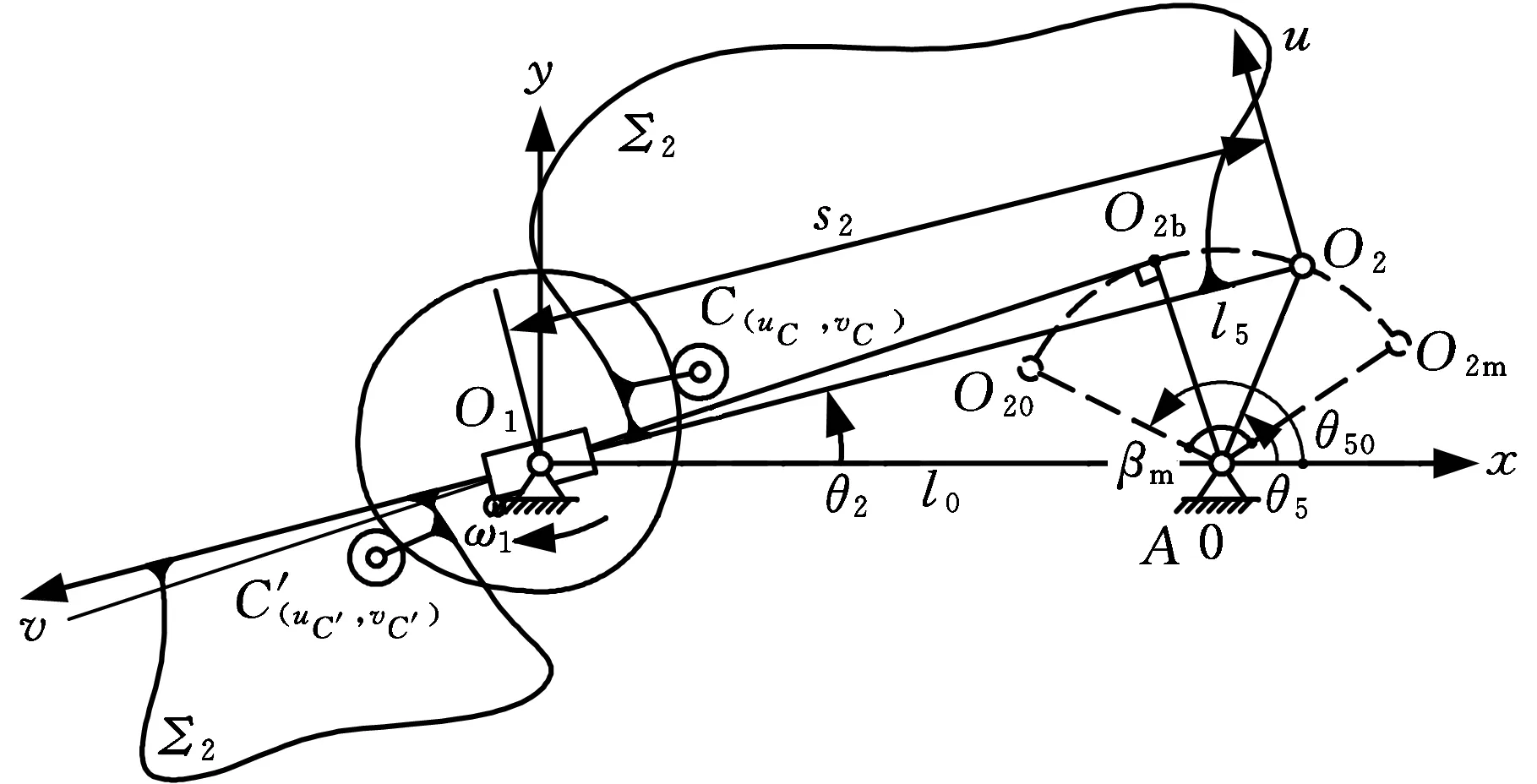
圖1 等跨凸輪機構Fig.1 Equal-span cam mechanism

圖2 諸運動角、休止角的牽連關系Fig.2 The implicated relations between the angles of motion and repose
值得指出:上述①~③,亦是等跨凸輪機構成立的充要條件。
往程中,凸輪主輪廓段作用于主滾子驅動機構運動,凸輪副輪廓段接觸副滾子起鎖合作用。返程中,則反之。
浮動滾子推桿等跨凸輪機構尺寸綜合問題的準確表述如下。
已知:機架、搖桿長度l0、l5,搖桿往程始/終位置O20A、O2mA,初位角θ50,行程角βm,往程運動規(guī)律β=β(θ1)(θ1為凸輪轉角),往程運動角Ф0,推程許用壓力角[α],凸輪、搖塊和機架在O1點復合鉸接。
求解:整程滿足壓力角α≤[α]和條件①~③的C、C′解集,r0許用取值范圍(r0為凸輪基圓半徑),最優(yōu)尺寸解等。
浮動滾子推桿等徑凸輪機構[2](圖3)滿足條件①~③,不過uC=-uC′=0。
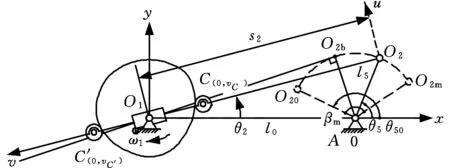
圖3 等徑凸輪機構Fig.3 Yoke radial cam mechanism
2 固定/浮動坐標系和解析公式
2.1 固定坐標系和解析公式
建立固定坐標系O1xy(圖1)。連桿2往程(返程)的時變長度和類角速度
s2(r)=s2(r)(θ1)=(l02+l52+2l0l5cos(θ50-β(r)))1/2
(1)
θ2(r)=arctan(l5sin(θ50-β(r))/(l0+l5cos(θ50-β(r))))
(2)
dθ2(r)/dθ1=-l5(dβ(r)/dθ1)(l5+l0cos(θ50-β(r)))/
(3)
絕對瞬心P20(r)、相對瞬心P21(r)往程(返程)坐標
(4)
(5)
式(5)中,“±”的“+”對應同擺式機構,“-”對應異擺式機構。
P20(r)、P21(r)至P10(O1)的距離
(6)
后文中,簡記lP10P20(r)、lP10P21(r)為l20(r)和l21(r)。
2.2 浮動坐標系的概念
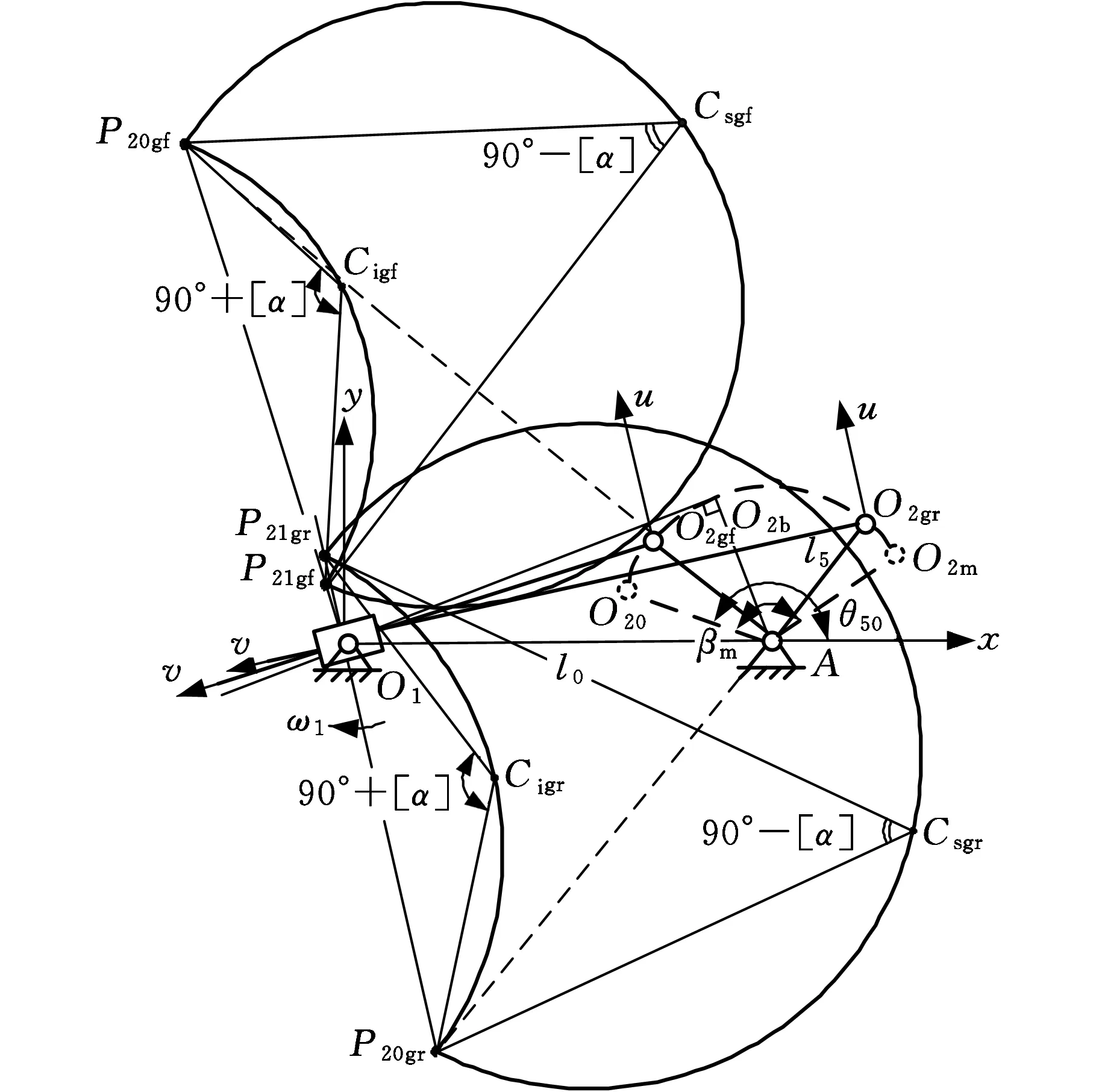
浮動坐標系(圖1)為固連于連桿平面Σ2、以O2為原點的直角坐標系O2uv[3]。
2.3 往程/返程的前半區(qū)段、后半區(qū)段劃分[2]
往程:搖桿5的行程O20A→O2mA。前半區(qū)段O20A→O2bA;后半區(qū)段O2bA→O2mA。
返程:搖桿5的行程O2mA→O20A。前半區(qū)段O2mA→O2bA;后半區(qū)段O2bA→O20A。
O2bO1⊥O2bA,即
(7)
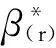
3 等跨凸輪機構的特征牽連關系
3.1 主/副滾子間的分布規(guī)律特征
(8)
據式(8)和條件③,得
s20-vC=vC′-s2m
(9)
即
vC′=s20+s2m-vC

圖4 主/副滾子間的分布規(guī)律特征Fig.4 The distribution characteristics of main roller and auxiliary roller
C和C′的u向跨距、v向跨距分別為
(10)
據式(9)、式(10)得到:C(uC,vC)一旦選定,Lu、Lv和C′(uC′,vC′)隨之確定,皆為定值。
3.2 諸運動角、休止角的牽連關系
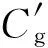
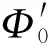
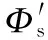
(11)
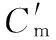
(12)
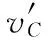
(13)
據式(12)得到:Ф0+Фs為定值,與C、C′位置選取無關。
搖桿位移規(guī)律:可自由任意選取范圍θ1∈[0, Ф0+Фs];而余下θ1∈(Ф0+Фs, 360°],須依據等跨機構條件①~③確定。
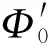
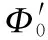
(14)
式(12)和式(14)中,“+”、“-”分別對應凸輪順時針、逆時針轉動情況。
3.3 搖桿返程位移規(guī)律

圖5 搖桿返程位移規(guī)律Fig.5 Return displacement law of rocker
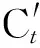
(15)
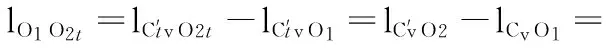
(16)
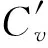
據余弦定理有
(17)

(18)
某時刻,凸輪轉過角度
θ1Δ=180°±(θ2-θ2t)
(19)
對應凸輪角位移
(20)
搖桿返程角位移
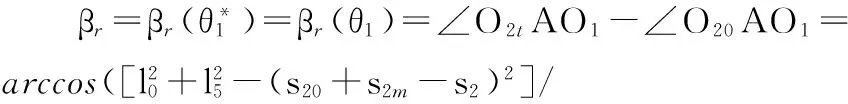
(21)
4 主/副滾子中心C、C′的整程區(qū)域套
4.1 滿足α≤[α]條件的C的整程區(qū)域套
滿足α≤[α]條件的C的解集即整程區(qū)域套,它主要取決于往程。
4.1.1 滿足α≤[α]條件的C的往程區(qū)域套
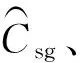
(22)

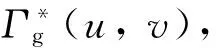
通常地,返程區(qū)域套因不起作用而免予考慮,往程區(qū)域套即整程區(qū)域套。
4.1.2 實際最經濟搜索帶域與等距離散化
據圖6a,ugmin、ugmax必出現(xiàn)在Γg(u,v)最左、最右端處,即
(23)
式中,η=1;前半區(qū)段ζ=1,后半區(qū)段ζ=-1。
通過一維搜索,可解得(ugmin)maxty、(ugmax)minty,其含義和求解方法見文獻[3]。
理論最經濟搜索帶域
ug∈[(ugmin)maxty, (ugmax)minty]
(24)
等距離散化該最經濟搜索帶域,得直線序列{ugj}。取間距
Δug=[(ugmax)minty-(ugmin)maxty]/(100q)
(25)
ugj=(ugmin)maxty+(j-1)Δug
(26)
j=1,2,…,100q+1
式中,q=1,2,…,據精度要求確定。
等距離散化θ1,間距
Δθ1=1/(10p-1) (rad)
(27)
θ1=θ1m=0°+(m-1)Δθ1
(28)
m=1,2,…,Ф0/Δθ1+1
式中,p=1,2,…,也據精度要求確定。
根據{?Γg(θ1m)},通過求交比較,得到實際最經濟搜索帶域:
ug∈[(ugmin)maxry,(ugmax)minry]
(29)
(a)往程瞬時區(qū)域套Γg(u, v)生成原理
(b) 往程區(qū)域套生成原理圖6 主滾子中心C的區(qū)域套生成原理Fig.6 The generating principle of nested region of main roller C
分析{ugj}與{?Γg(θ1m)}的關系如下:

設{ugj}與O1P21交于Oj點(圖7僅表述ugfmin
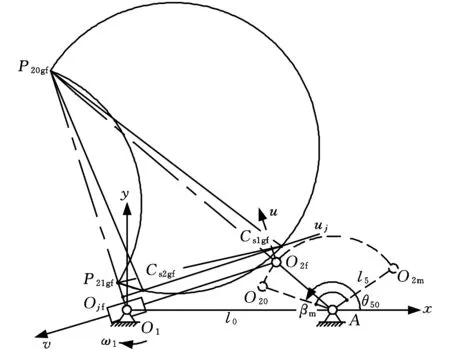
圖求解的解析公式建立Fig.7 Establishment of analytic formula for
對于關系(1)和(2),分別有
(30)
(31)
下面分ugj≤0、ugj>0兩種情況討論。
(1)ugj≤0。
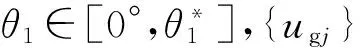
(32)
解得
τCs1g={(l20-l21)tan[α]+[(l20-l21)2tan2[α]-
4(l20-ηugj)(l21-ηugj)]1/2}/2
(33)
τCs2g={(l20-l21)tan[α]-[(l20-l21)2tan2[α]-
4(l20-ηugj)(l21-ηugj)]1/2}/2
(34)
將式(1)、式(33)和式(34)代入式(30),搜索解得
vCs1gflmax=(s2-τCs1g)flmax
vCs2gflmin=(s2-τCs2g)flmin
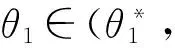
(35)
(36)
解得
τCs1g={(l20+l21)tan[α]+[(l20+l21)2tan2[α]+
4(l20+ηugj)(l21-ηugj)]1/2}/2
(37)
τCi2g={-(l20+l21)tan[α]+[(l20+l21)2tan2[α]+
4(l20+ηugj)(l21-ηugj)]1/2}/2
(38)
將式(1)、式(37)和式(38)代入式(31),搜索解得
vCs1grmmax=(s2-τCs1g)rmmax
vCi2grmmin=(s2-τCi2g)rmmin
(2)ugj>0。
先令
l21(θ1)-ugj=0
(39)
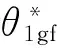
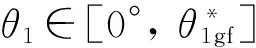
(40)
(41)
解得
τCs1g={(l20-l21)tan[α]+[(l20-l21)2tan2[α]+
4(l20-ηugj)(ηugj-l21)]1/2}/2
(42)
τCi2g={-(l20-l21)tan[α]+[(l20-l21)2tan2[α]+
4(l20-ηugj)(ηugj-l21)]1/2}/2
(43)
將式(1)、式(42)和式(43)代入式(31),搜索解得
vCs1gfmmax=(s2-τCs1g)fmmax
vCi2gfmmin=(s2-τCi2g)fmmin

vCs1gflmax=(s2-τCs1g)flmax
vCs2gflmin=(s2-τCs2g)flmin
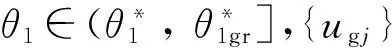
vCs1grmmax=(s2-τCs1g)rmmax
vCi2grmmin=(s2-τCi2g)rmmin

(44)
解得
τCs1g={(l20+l21)tan[α]+[(l20+l21)2tan2[α]-
4(l20+ηugj)(ηugj-l21)]1/2}/2
(45)
τCs2g={(l20+l21)tan[α]-[(l20+l21)2tan2[α]-
4(l20+ηugj)(ηugj-l21)]1/2}/2
(46)
將式(1)、式(45)和式(46)代入式(30),搜索解得
vCs1grlmax=(s2-τCs1g)rlmax
vCs2grlmin=(s2-τCs2g)rlmin
據上述計算結果,得到:
①ugj≤0時
(47)
②ugj>0時
(48)
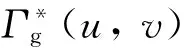
4.2 滿足α≤[α]條件的C′的整程區(qū)域套
4.2.1 滿足α≤[α]條件的C′的返程區(qū)域套
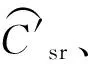
(49)
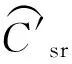
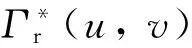
通常,往程區(qū)域套不起作用,故返程區(qū)域套即整程區(qū)域套。
4.2.2 實際最經濟搜索帶域
式(23)~式(27)中,將ug、(ugmin)maxty、(ugmax)minty替以ur、(urmin)maxty、(urmax)minty;式(23)取η=-1,將l20、l21替以l20r、l21r。其中:
θ1=θ1n=Ф0+Фs+(n-1)Δθ1
(50)
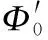
即可得到實際最經濟搜索帶域
ur∈[(urmin)maxry, (urmax)minry]
(51)

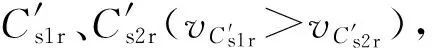
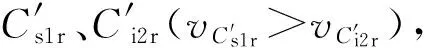
(a)返程瞬時區(qū)域套Γr(u, v)生成原理
(b)返程區(qū)域套生成原理圖8 副滾子中心C′的區(qū)域套生成原理Fig.8 The generating principle of nested region of auxiliary roller C′
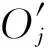
對應關系(1)和(2),分別有
(52)
(53)
(1)urj≥0。
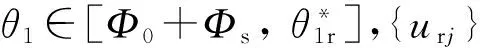

(2)urj<0。
令
l21r(θ1)-urj=0
(54)
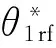
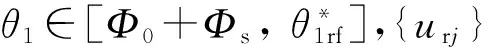
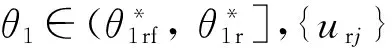

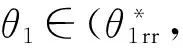
據上述計算結果可得
①urj≥0時
(55)
②urj<0時
(56)

5 滿足α≤[α]和等跨條件①~③的C、C′的整程區(qū)域套以及凸輪基圓半徑r0取值范圍的確定
本節(jié)討論凸輪順時針轉動時,滿足α≤[α]和等跨條件①~③的C、C′的整程區(qū)域套。凸輪逆時針轉動時的情況與順時針轉動時類似,不再詳述。
5.1 主/副滾子中心C、C′的歸并搜索帶域
如圖9所示,據式(29)和式(51)進行歸并求交,得到滿足α≤[α]和等跨條件①~③的C、C′的歸并搜索帶域。
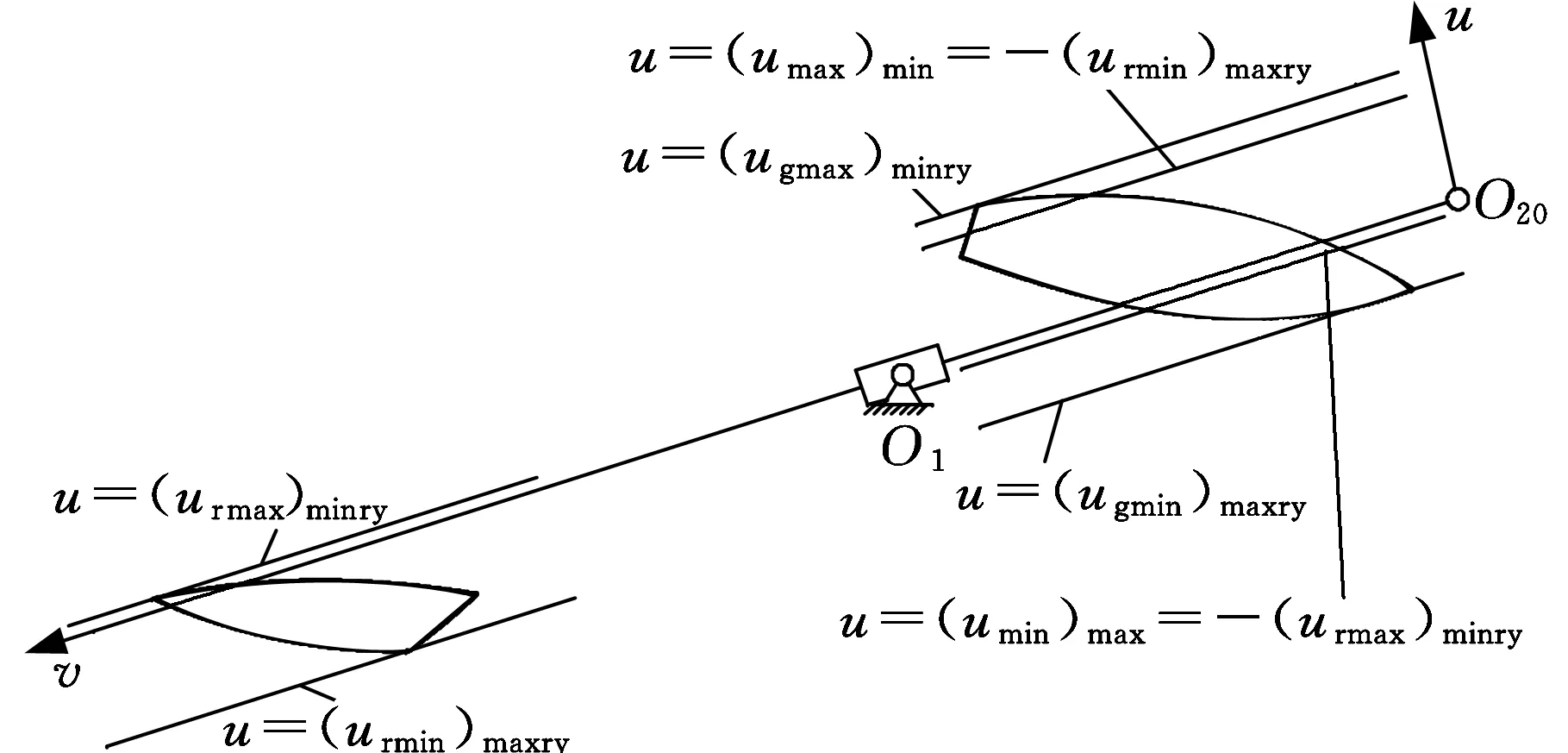
圖9 C、C′歸并搜索帶域的確定Fig.9 Determination of merger search belt-area of C and C′
主滾子中心C的歸并搜索帶域
uC∈[(umin)max, (umax)min]
(57)
(58)
副滾子中心C′的歸并搜索帶域
uC′∈[-(umax)min, -(umin)max]
(59)
5.2 主/副滾子中心C、C′的整程區(qū)間套
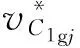
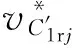

(60)
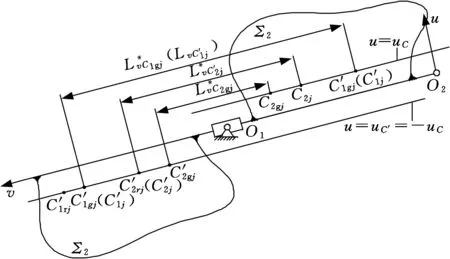
圖10 C、C′整程區(qū)間套的確定Fig.10 determination of merger whole choice area of C and C′
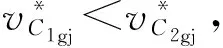
通過求交,得到u=urj=uC′(=-uC)時副滾子中心C′的歸并整程區(qū)間套
(61)
(62)
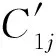
(63)
則
(64)
即為u=ugj=uC時主滾子中心C的歸并整程區(qū)間套。
上述式(61)和式(64)的獲取,體現(xiàn)了一個正-逆映射求交的迭代求解過程,這也是本文的核心內容。
5.3 主/副滾子中心C、C′的歸并整程區(qū)域套
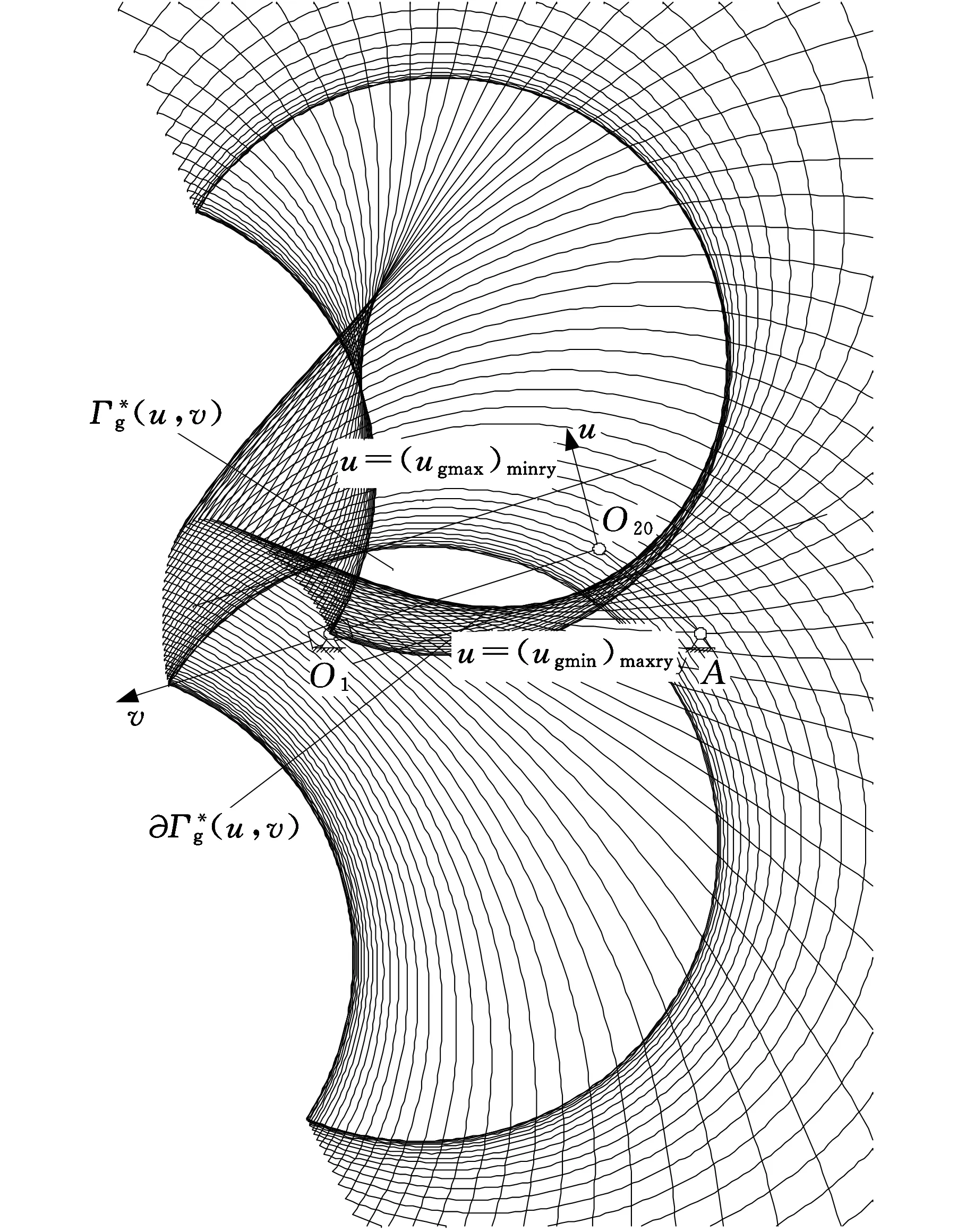
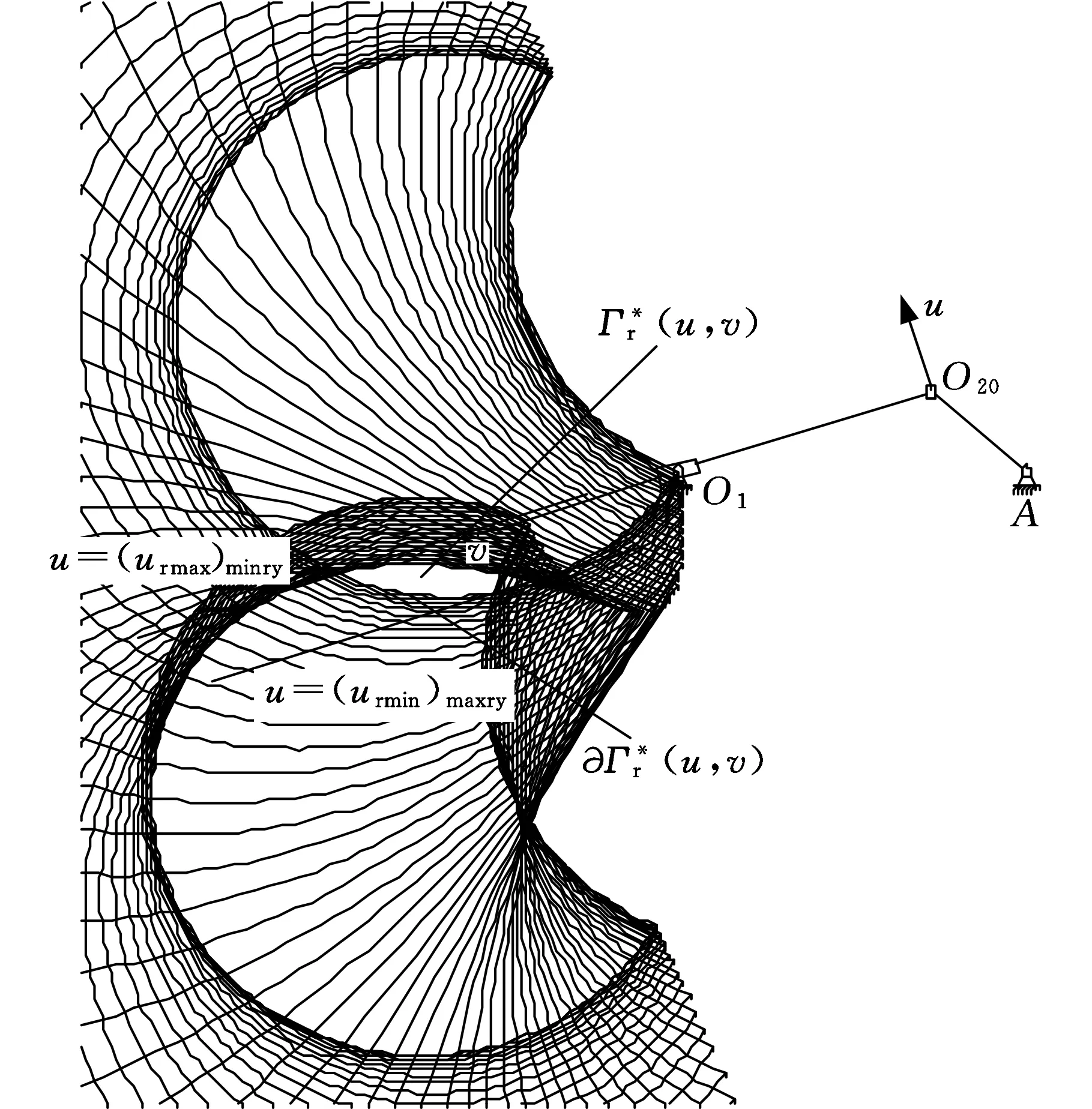
據式(57)、式(59)和式(61)、式(64),遍歷搜索{ugj}和{urj},解得C、C′的歸并整程區(qū)域套Γ*(u,v)和Γ′*(u,v),以及C、C′的歸并整程區(qū)域套邊界?Γ*(u,v)、?Γ′*(u,v),如圖11所示。
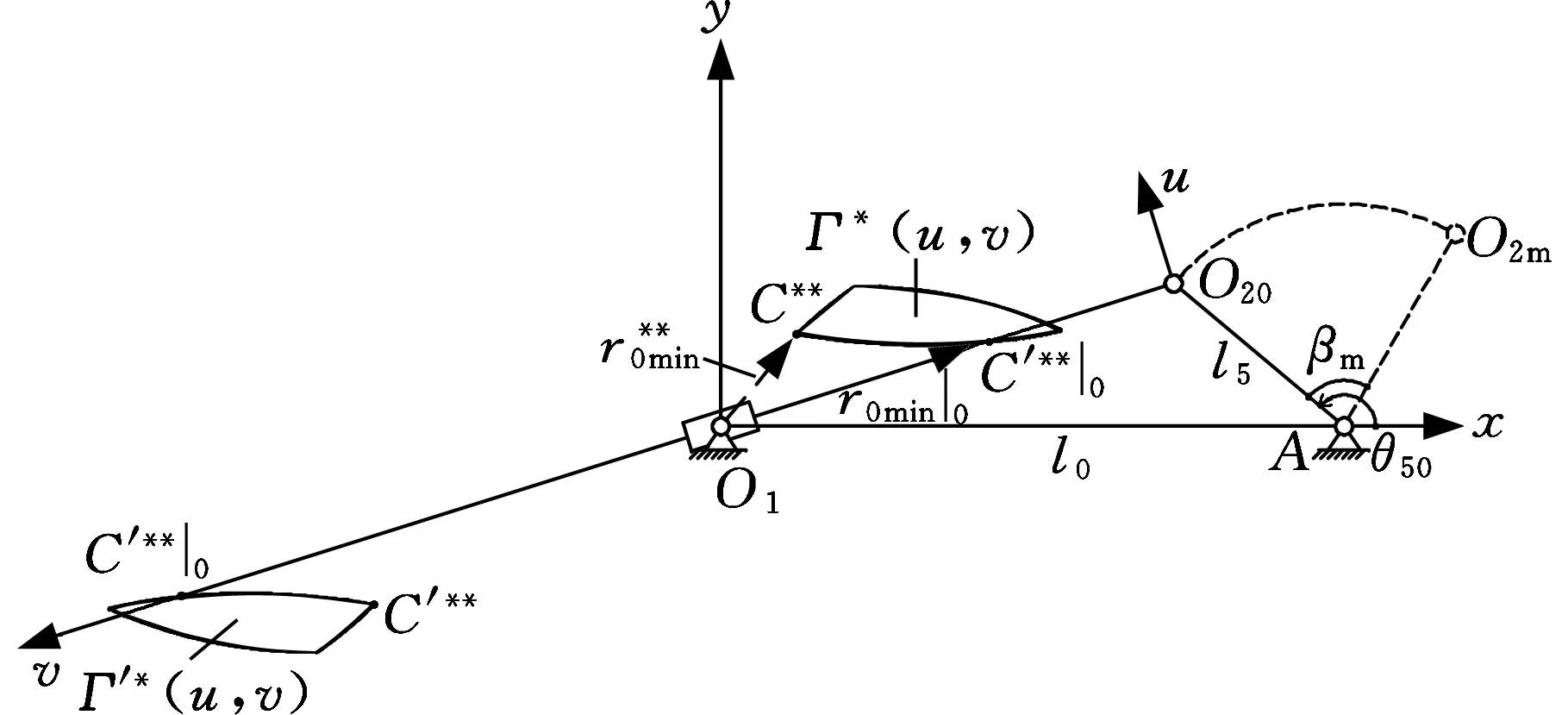
圖11 整程區(qū)域套Γ*(u, v)、Γ′*(u, v)的形態(tài)分布Fig.11 Morphological distribution of merger whole choice area of Γ*(u,v)、Γ′*(u,v)
圖11中的Γ*(u,v)和Γ′*(u,v),可采用開發(fā)的ESCMFY可視化程序,結合例題已知條件,在計算機上快速求解得到。
5.4 凸輪基圓半徑r0取值范圍的確定
引入O2uv到O1xy的坐標變換
(65)
C在?Γ*(u,v)上時,凸輪基圓半徑
(66)
一維搜索解得所有邊界點(xCj,yCj),計算得到凸輪最小、最大基圓半徑:
(67)
r0的取值范圍為
(68)
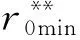
6 機構綜合示例
對于浮動滾子推桿等跨凸輪機構,已知l0=140 mm,l5=50 mm,θ50=140°,βm=80°,往程選取擺線規(guī)律,Ф0=150°,[α]=40°,凸輪順時針轉動。求解:
(1)取uC=uC′=0,即等徑凸輪機構,限定C、C′居于連桿方位線O1O2上,對應的求解量為r0min|0、C**|0和C′**|0;

(3)比較討論(1)、(2)的求解結果。
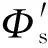
(1)令uC=uC′=0,即等徑凸輪機構,據式(64)解得vC|0∈[29.8963, 43.7701]mm、r0|0∈[62.8853,76.7591]mm,即r0min|0=62.8853 mm。對應有,C**|0(0, 43.7701)mm和C′**|0(0, 233.4725)mm。
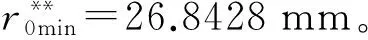
7 結論
(1)提出浮動滾子推桿等跨凸輪機構新構型,給出尺寸綜合問題的準確描述;提出其形態(tài)特征與條件,揭示與等徑凸輪機構的聯(lián)系與差異。
(2)討論解決了主/副滾子分布規(guī)律特征,運動角、休止角的牽連關系,搖桿返程位移規(guī)律等。
(3)通過主/副滾子中心歸并搜索帶域和歸并整程區(qū)域套的正-逆映射求交的求解過程,揭示等跨凸輪機構復雜、獨到的異質性研究內涵。
(4)通過對比等跨、等徑凸輪機構的尺寸綜合結果,充分論證了等跨凸輪機構的引入具有重要的機構學理論意義和工程實際價值。
[1] 常勇, 楊富富. 作平面運動滾子從動件盤形凸輪機構的第Ⅱ類機構綜合問題[J]. 機械工程學報, 2010,46(21):35-41. CHANG Yong, YANG Fufu. Second Mechanism Synthesis Task of Disc Cam Mechanisms with Roller Follower Moving in Planar General Motion[J]. Journal of Mechanical Engineering,2010,46(21):35-41.
[2] 常勇, 楊富富. 作平面運動滾子從動件形鎖合凸輪機構的第Ⅱ類機構綜合問題[J]. 機械工程學報,2012,48(1):39-46. CHANG Yong, YANG Fufu. Second Mechanisms Synthesis Task of Positive-drive Disc Cam Mechanisms with Roller Follower Moving in General Planar Motion[J]. Journal of Mechanical Engineering,2012,48(1):39-46.
[3] 常勇, 楊富富, 胡志超, 等. 作平面運動滾子從動件盤形凸輪機構的廣義第Ⅱ類機構綜合問題[J]. 機械工程學報,2012,48(15):47-57. CHANG Yong, YANG Fufu, Hu Zhichao, et al. Research on the General Second Mechanisms Synthesis Task of Disc Cam Mechanisms with Roller Follower Moving in General Planar Motion[J]. Journal of Mechanical Engineering,2012,48(15):47-57.
[4] 常勇, 吳秋平, 陳續(xù)揚,等. 負半徑滾子直動推桿盤形凸輪機構的可視映射尺度綜合與比較優(yōu)勢[J]. 機械工程學報,2017,53(1):36-46. CHANG Yong,WU Qiuping, CHEN Xuyang, et al. Dimension Synthesis of Cam Mechanisms with Negative Radius Follower Based on Technology of the Visualization-oriented Mapping and Comparative Advantage[J]. Journal of Mechanical Engineering,2017,53(1):36-46.
[5] 常勇, 林榮富, 李延平. 作平面運動滾子從動件盤形凸輪機構的深度廣義第Ⅱ類綜合問題[J]. 中國機械工程,2014,25(16):2149-2158. CHANG Yong, LIN Rongfu, LI Yanping. Deep General Class Ⅱ Synthesis of Disc Cam Mechanism with Roller Follower Moving in Planar Motion[J]. China Mechanical Engineering,2014,25(16):2149-2158.
[6] 常勇, 林榮富, 李延平. 做平面運動滾子從動件盤形凸輪機構第Ⅱ類綜合問題的廣義化研究[J]. 中國機械工程, 2014,25(5):669-678. CHANG Yong, LIN Rongfu, LI Yanping. General Class ⅡSynthesis of Disc Cam Mechanism with Roller Follower Moving in General Motion[J]. Chinese Mechanical Engineering,2014,25(5):669-678.
[7] 常勇, 林榮富, 李延平. 浮動平底推桿共軛凸輪機構的第Ⅱ類機構綜合問題研究[J]. 農業(yè)機械學報,2014,45(3):333-340. CHANG Yong, LIN Rongfu, LI Yanping. Class Ⅱ Synthesis of Conjugate Cam Mechanism with Floating Flat Faced Pushrod[J]. Transactions of the Chinese Society for Agricultural Machinery,2014,45(3):333-340.
[8] SCHOENHERR J. Synthesis of Planar Cam Mechanisms with Lowest Dimensions[J]. Mechanism and Machine Theory,1993,28(3):317-325.
[9] DASGUPTA A, GHOSH A. On the Determination of Basic Dimensions of a Cam with a Translating Roller-follower[J]. Journal of Mechanical Design, Trans. of ASME,2004,126(1):143-147.

