基于Chebyshev區間方法的動力總成懸置系統穩健性優化

陳 劍 李士愛 劉 策 鄧支強 舒宏超

合肥工業大學噪聲振動研究所，合肥,230009

0 引言

動力總成懸置系統是汽車振動系統中一個重要子系統，起著支撐部件和隔離振動的作用。懸置系統設計的優劣對整車的NVH(noise，vibration，harshness)性能有重大影響，對懸置系統進行合理的設計可有效地降低汽車的振動噪聲，因此，動力總成懸置系統的優化設計對整車的NVH性能極為重要。而動力總成懸置系統設計的基本任務就是進行動力總成剛體振動模態的頻率配置和解耦布置[1-3]。

傳統的分析和設計只是假定懸置系統參數為確定值而進行的確定性研究[1-3]，然而在懸置系統各零部件的制造、安裝及其系統的使用過程中，各懸置元件的剛度、位置、角度等影響整車振動的關鍵性參數會不可避免地出現一定程度的偏差或波動，故傳統方式可能會導致不恰當的設計。目前常用的研究非確定性問題的方法有概率方法(隨機方法)、模糊方法和區間分析方法等。沈忠亮[4]將懸置剛度、安裝位置和角度等參數作為正態隨機變量，對懸置系統的解耦率應用多目標粒子群算法進行了穩健性優化設計。吳杰等[5-6]采用區間數對懸置元件剛度參數變化的不確定性進行描述，提出了改進區間截斷方法，并對懸置系統固有頻率和解耦率變化范圍進行了計算。相比較而言，獲得不確定參數的變化范圍通常比得到不確定參數真實的統計特性和模糊數的隸屬度函數容易，邱志平等[7-8]通過實例對區間分析方法和概率方法進行了比較，結果表明區間分析方法結果有效且包括更多的可能解。

本文應用基于區間數學和Chebyshev理論建立的區間分析方法，分別計算動力總成懸置系統固有頻率和解耦率隨懸置剛度波動的變化范圍，并利用區間型穩健優化方法對系統的解耦率和頻率進行穩健性優化分析。

1 基本理論

1.1 Chebyshev區間分析方法

區間分析方法有廣泛的工程實際背景。Chebyshev區間方法是由吳景錸等[9-10]提出的。k階一維Chebyshev級數在x∈[a,b]內用Ck(x)表示，其關系表達式如下：

Ck(x)=coskθ

(1)

當x∈[-1,1]時，Chebyshev級數存在以下的遞推關系：

(2)

正交性是Chebyshev級數的一個重要性質，即對于k階Chebyshev級數Ck(x)和p階Chebyshev級數Cp(x)，有

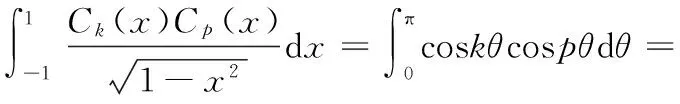
(3)

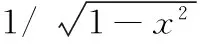
設存在函數f(x)∈C[a,b]，則它可用一個基于Chebyshev級數Ci(x)的k階多項式pk(x)來近似的表示，即有

(4)

式中，f0、fi均為常系數。

這是將原函數展開成多項式，利用區間算法計算各項的值，再進行求和計算原函數的擴張區間。因此可將式(4)中的變量x替換為區間變量[x]，則區間函數[fCn]([x])為

(5)

由于[θ]=[0,π]，對于k>0的Chebyshev級數恒有Ck([x])=[cos](k[θ])=[-1,1]，因此式(4)可進一步變換為

(6)

只要計算表達式中的系數函數fi，就可以得到函數的區間。根據Chebyshev區間方法的正交性和Gaussie-Chebyshev求積分公式可推導出下式：

(7)

式中，xj為插值點。

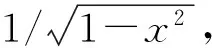
xj=cosθj

將一維問題延伸至多維問題。n維Chebyshev多項式對x∈[-1,1]n定義為每一維Chebyshev多項式的張量積：

Ck1,k2,…,kn(x1,x2,…,xn)=cosk1θ1cosk2θ2…cosknθn

(8)

其中，θi=arccosxi∈[0,π]。則

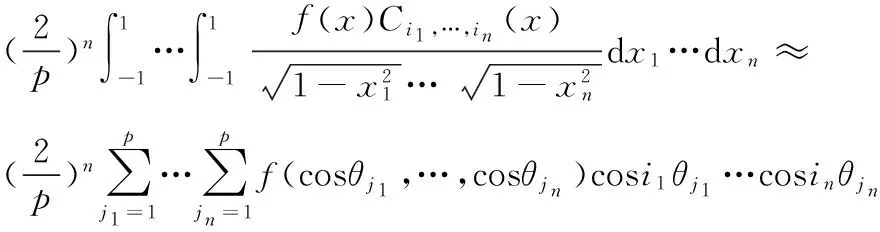
(9)

考慮式(6)，則k階Chebyshev擴張函數為

(10)

其中，l等于n維Chebyshev級數Ci1,…,ik(x)的下標中包含0的個數，例如，C0,0(x)對應的l=2,而C2,1(x)對應的l=0等。

1.2 誤差分析

Chebyshev區間方法的誤差來源主要有[10]：

(1)在區間運算過程中，由于區間算法規則本身具有包裹效應易發生區間擴張現象，使得計算的參數區間大于真實區間。

(2)近似為多項式時的截斷誤差。如果函數f(x)具有k+1階連續導數，則近似的截斷誤差為

(11)

由式(11)可知，k越大，截斷誤差越小，因此k足夠大時，該誤差可忽略。

(3)計算系數時的數值積分誤差。積分公式的誤差可表示為

(12)

式中，ξ為[-1,1]的任意數。

則當插值積分公式中的最髙階次p足夠大時，該積分誤差即可忽略。由于求插值點數量不能少于未知數個數，故參數p取值不應小于k+1。當k較大時，截斷誤差和數值積分誤差都較小，且該誤差的大部分影響會湮沒在低階項部分中，因此它對計算精度的影響基本可忽略。

而Chebyshev級數在區間算法中采用了三角函數表達式[10]，能更有效地控制區間算法的包裹效應，從而更接近于實際的上下界限。

1.3 頻率和解耦率的Chebyshev區間分析方法

應用Chebyshev區間分析方法對動力總成懸置系統的固有頻率和解耦率隨懸置參數波動的區間范圍的求解過程如圖1所示。

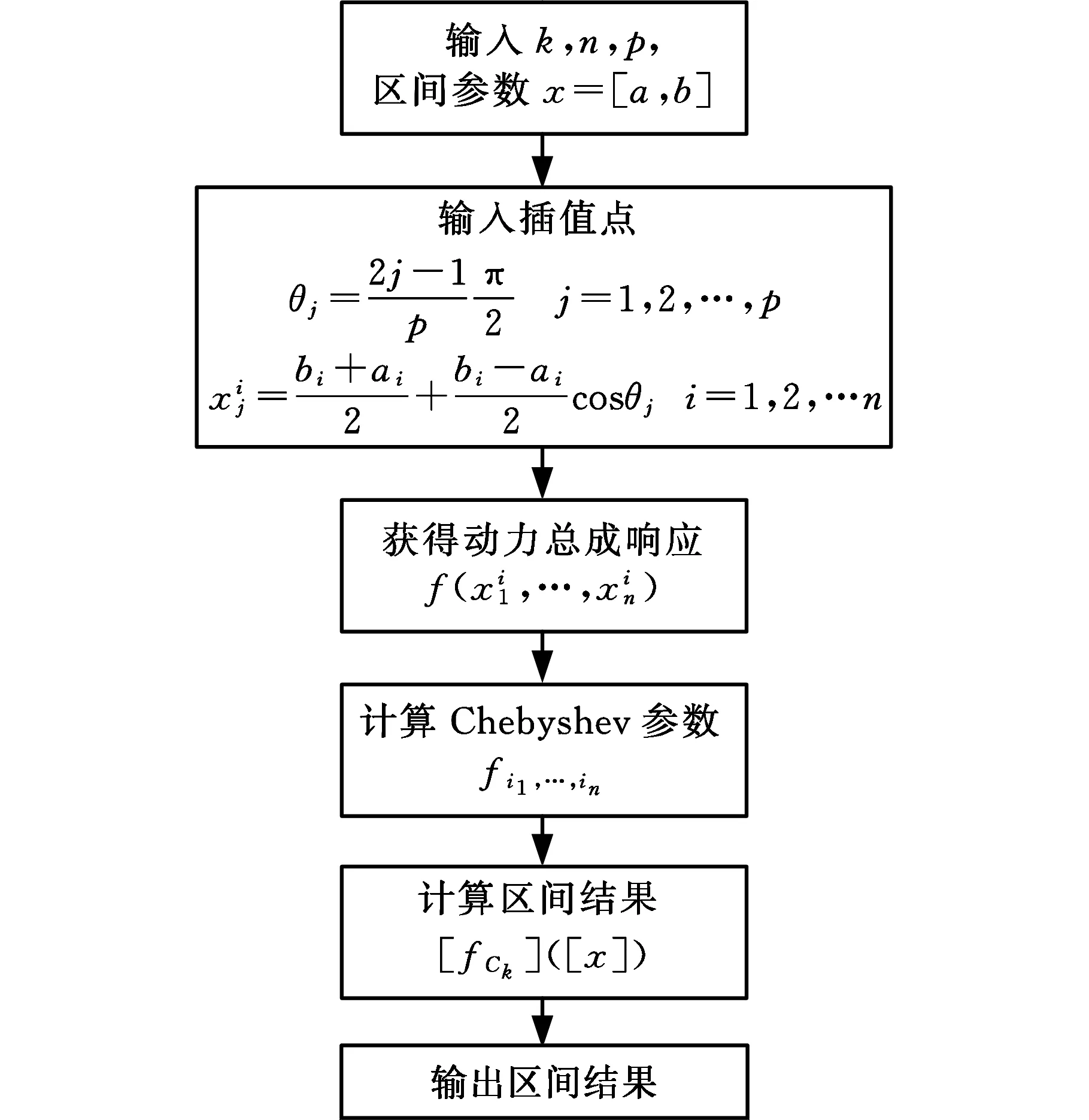
圖1 Chebyshey區間分析方法流程圖Fig.1 Flow chart of Chebyshey interval analysis method

2 固有頻率和解耦率的區間優化模型

整車對動力總成系統安裝位置的限制較為嚴格，尤其對于改進車輛，一般不改變各懸置的安裝位置坐標和安裝角度，因此常選擇懸置剛度作為優化設計變量。為了獲得更為穩健的懸置系統的固有頻率和解耦率，在進行優化設計時，應綜合考慮各種不確定因素導致關鍵參數的變化對優化結果可能產生的影響。為此提出區間優化方法，考慮最優設計參數發生波動時進行穩健優化設計[12]。

傳統優化模型只考慮獲得盡量高的解耦率，區間優化模型還需要使解耦率變化區間隨剛度參數波動變化半徑最小，從而保證各解耦率的穩健性。

懸置系統解耦率的區間優化模型為

(13)

區間優化采用遺傳算法[13]對穩健優化模型進行全局優化計算，以區間優化模型為遺傳算法的適應度函數，以懸置各剛度值為設計變量，尋優計算得到穩健可靠的優化解。

3 算例

根據某型待改進汽車動力總成懸置系統具體情況，同時考慮動力總成剛體模態固有頻率遠低于其彈性模態固有頻率，可將動力總成作為剛體考慮。因此可將發動機懸置系統簡化為：通過若干個三維黏-彈性懸置元件支承于車架上的具有6個自由度的模型。算例為四點平置式懸置，其布置如圖2所示。動力總成的坐標系原點選在總成質心處，X軸平行于曲軸中心線，指向發動機前端，Z軸平行于氣缸中心線，指向發動機缸蓋，Y軸按正交坐標系的右手定則確定，懸置元件的三向剛度軸(u、v、w)分別與參考坐標系軸(X軸、Y軸、Z軸)平行。

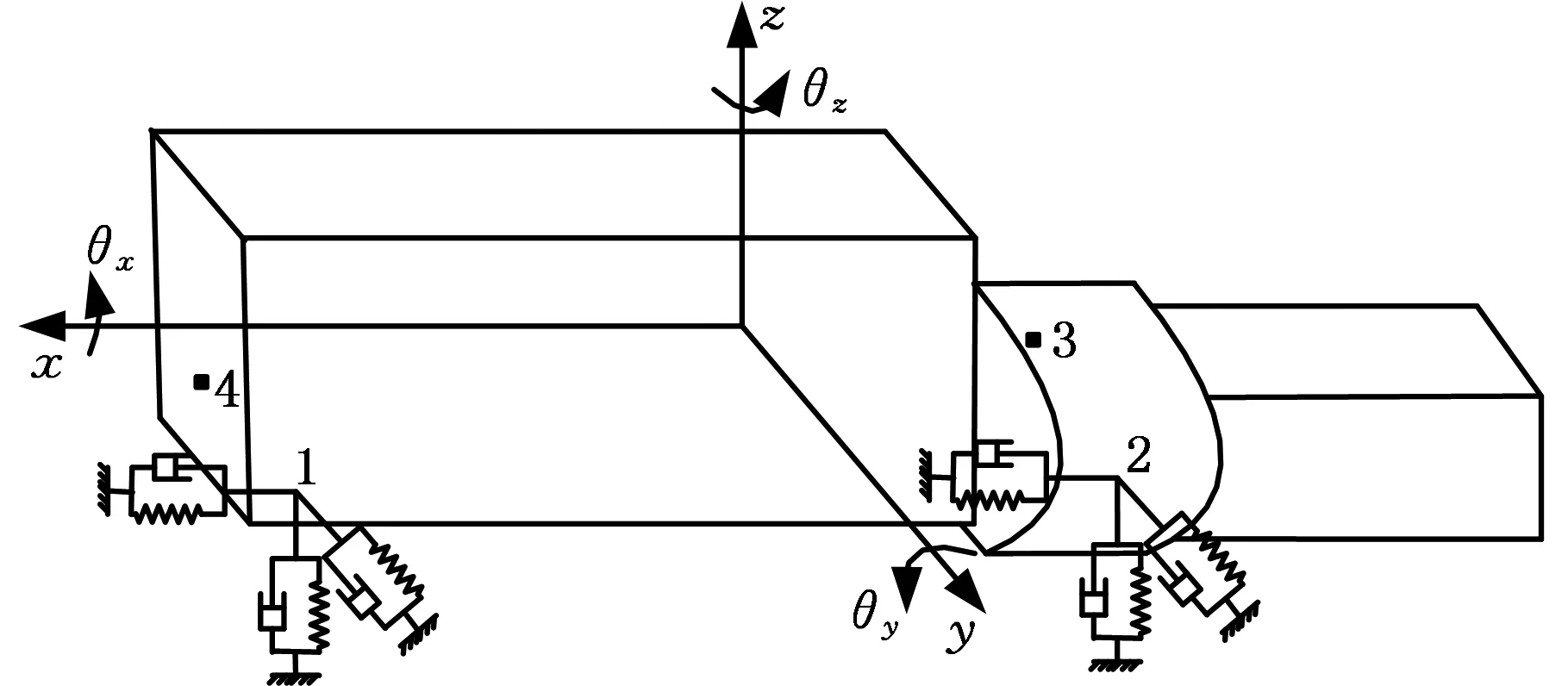
圖2 動力總成懸置系統的六自由度模型Fig.2 The six degrees of freedom of the powertrain mounting system

表1和表2給出了動力總成系統的總質量m、質心坐標(x0,y0,z0)以及轉動慣量和慣性積。表3所示為懸置元件的初始靜剛度，一般為經驗值。

表1 動力總成質量和質心位置坐標

表2 動力總成系統的轉動慣量和慣性積

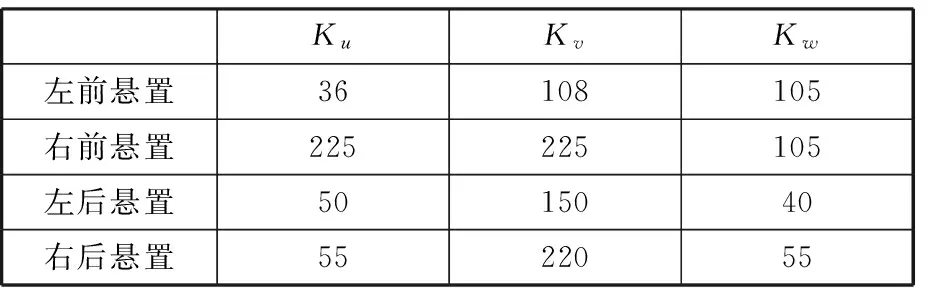
表3 懸置元件主軸方向初始靜剛度

優化前懸置系統固有頻率和振動解耦率計算結果如表4所示。由表4可以看出，各階固有頻率分布較合理，振動解耦率除x、z方向較理想外，其他方向振動耦合較嚴重，有待優化。

為減小計算量，選擇其中靈敏度大的重要參數作為設計參數，可以用二階響應面分析法或者最小二乘擬合法得到設計參數的精確表達式。

基于正交實驗法進行懸置剛度靈敏度分析，左前懸置u向剛度和右后懸置u、w向剛度對懸置系統的垂向和側傾方向解耦率都比較敏感，是系統解耦度設計指標的敏感因素，進行優化設計時應著重考慮，即將該3個不確定因素作為設計參數。表5所示為按照流程圖中公式計算3個設計參數的插值點。

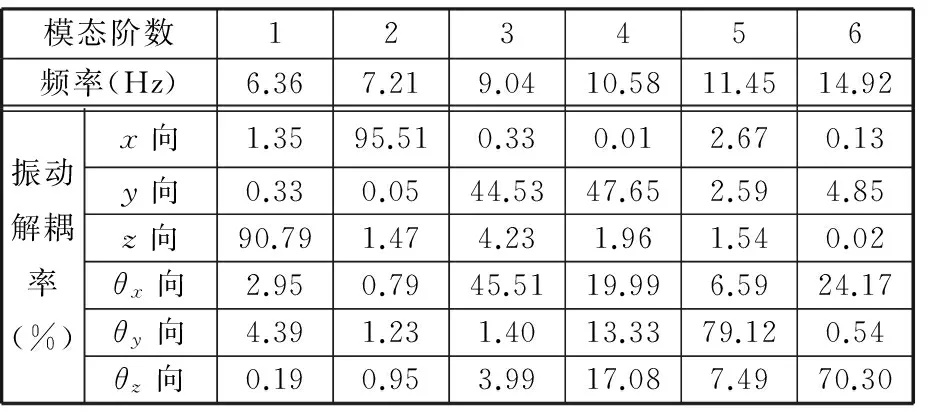
表4 優化前懸置系統固有頻率和能量解耦率

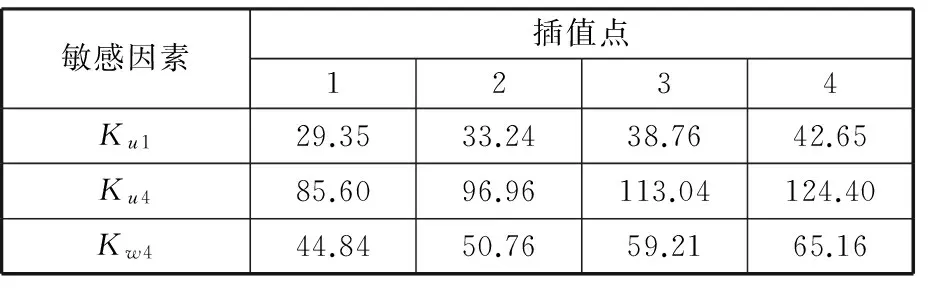
表5 Chebyshev插值點

為了避開該車其他部分的固有頻率和其他激振引起的共振，取懸置系統6個固有頻率的約束界限分別為5～18 Hz，9～16 Hz，5～18 Hz，6～15 Hz，10～18 Hz，10～18 Hz。

用Chebyshev區間分析方法和文獻[5]中改進區間截斷分析方法分別計算優化前固有頻率和解耦率區間變動量，圖3為部分模態方向解耦率區間的對比結果圖。由圖3可以看出，Chebyshev區間分析方法獲得的區間結果包裹性明顯更強，精度更高。圖3同樣說明了優化前系統的解耦率較小，且區間半徑較大，表明該懸置系統性能的穩健性較差，需對系統進行優化設計，即進行懸置剛度的優化匹配。

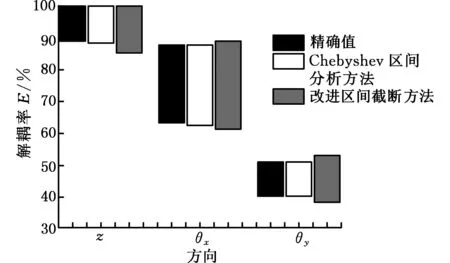
圖3 優化前懸置系統部分解耦率的區間分析結果Fig.3 A part of the result of interval analysis of the decoupling ratio of the powertrain mounting system before the optimization

表6所示為優化后當確定性優化最優剛度值和Chebyshev區間優化最優剛度值發生波動時懸置系統解耦率和固有頻率的變化區間。

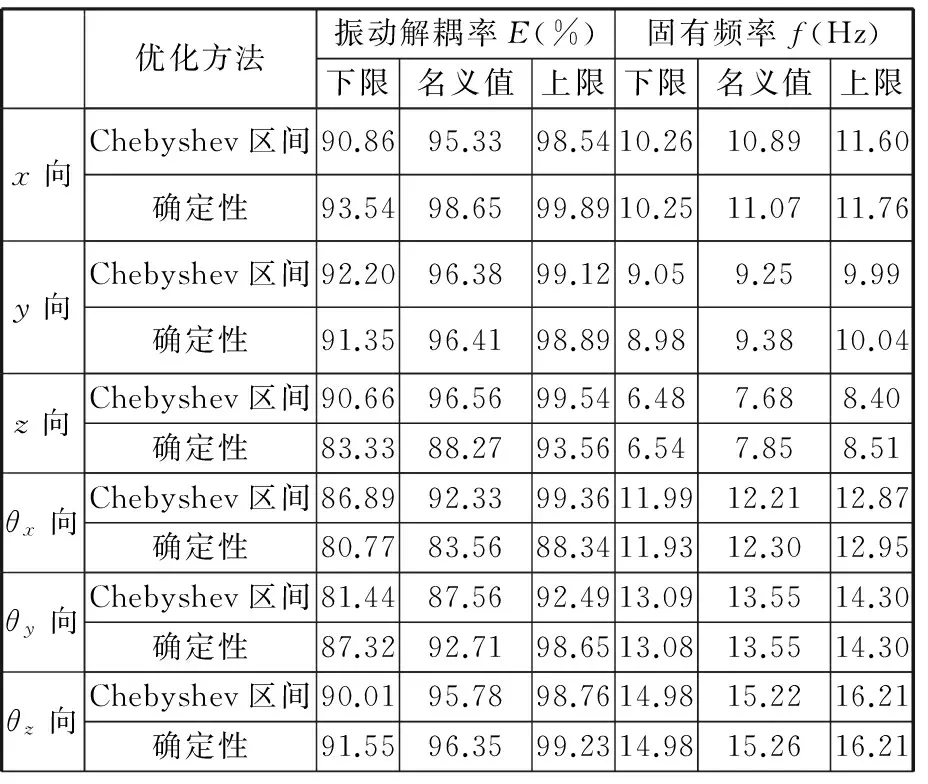
表6 優化后懸置系統解耦率和固有頻率的變化區間

由表6可以看出，Chebyshev區間優化方法較大程度地提高了懸置系統的解耦率，在z和θx方向尤為明顯。

由于在Chebyshev區間優化模型中考慮了解耦率的穩健性要求，所以不可避免地導致部分解耦率比確定性優化稍低。但Chebyshev區間優化方法的各階固有頻率區間范圍更小，分配更合理，且Chebyshev區間優化方法固有頻率的下限值更高、上限值更低，從而可以提高各頻率約束條件的區間概率度，即穩健性。

表7給出了在確定性優化和Chebyshev區間優化最優剛度值處，文獻[11]中所述的懸置系統頻率約束條件的左右區間概率度。由表7可以看出，最優剛度值波動時，Chebyshev區間優化最優剛度值處的左右區間概率度均大于或等于確定性優化，且穩健性較確定性優化有較大幅度提高，在y方向尤為明顯。

振動傳遞率能夠較好地反映動力總成通過懸置傳遞給車身的振動量的大小，振動傳遞量大說明隔振效果差，反之則好。對優化前后的懸置系統，利用ADAMS軟件可進行較為真實的振動仿真，從而實現分析比較。圖4、圖5所示分別為動力總成在怠速時，優化前后的懸置系統垂向和側傾方向的振動傳遞率。

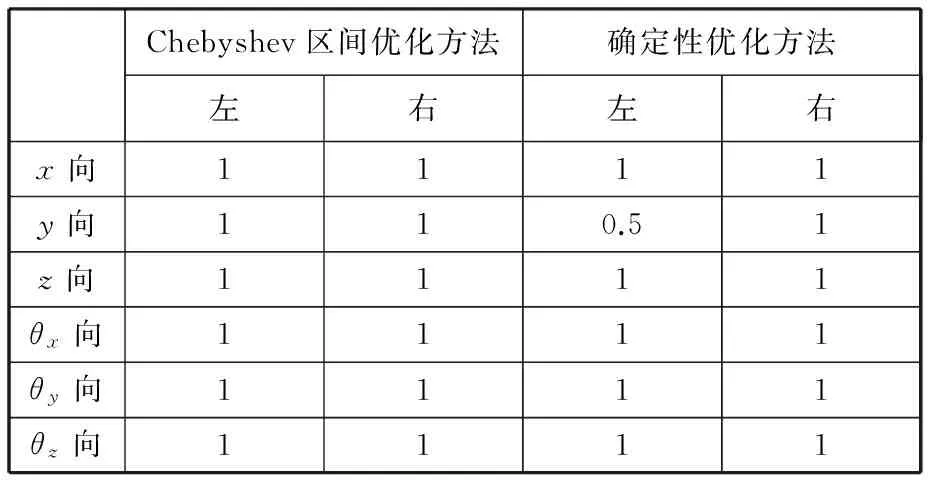
表7 優化后懸置系統頻率約束的區間概率度Tab.7 The interval probability of the frequency constraint of the powertrain mounting system is optimized

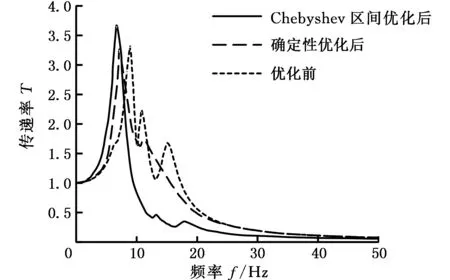
圖4 優化前后垂向的振動傳遞率Fig.4 The vibration transfer rate of z-direction before and after the optimization

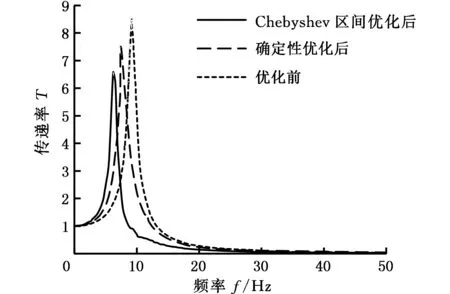
圖5 優化前后側傾方向的振動傳遞率Fig.5 The vibration transfer rate of the θx-direction before and after the optimization

由圖4、圖5可以看出，Chebyshev區間優化后懸置系統的振動傳遞率較優化前有較大改進。主要表現為:在垂直z方向上優化后系統振動傳遞率明顯較優化前有所減小，振動傳遞率峰值所對應的頻率也往低頻方向有所偏移(即由8.9 Hz變為6.7 Hz)，從而避開了懸置系統的固有頻率，且怠速激勵的系統振動傳遞率明顯小于1，有利于系統隔振；同時，側傾方向上的振動傳遞率也明顯地減小。而確定性優化后懸置系統的振動傳遞率改進效果不明顯，尤其是垂向上怠速激勵下的系統振動傳遞率明顯不小于1，這對系統的隔振不利。

可見，采用基于Chebyshev區間分析方法進行懸置系統參數優化后，振動解耦率、固有頻率分配和振動解耦率均取得較滿意的結果。

4 結論

(1)應用Chebyshev區間分析方法求解了懸置系統解耦率和固有頻率變動范圍。以高解耦率和解耦率變動范圍最小為優化目標，建立優化設計模型，實例驗證了該模型的可行性。

(2)Chebyshev區間分析方法只需不確定參數的變化范圍，而不需要獲得其概率分布，因此該方法相較于確定性方法更具有實際工程意義。

(3)Chebyshev區間分析方法誤差小，擴張效應不明顯，能更加準確地近似于真實區間。

(4)應用Chebyshev區間分析方法的優化模型不僅能夠明顯提高系統振動能量解耦率以及穩健性，還能有效改善敏感方向振動傳遞率。

[1] 呂振華，范讓林.動力總成懸置系統振動解耦設計方法[J].機械工程學報,2005，41(4):49-54. LYU Zhenhua，FAN Ranglin. Design Method for Vibration Uncoupling of Powertrain Mounting System[J]. Journal of Mechanical Engineering,2005，41(4):49-54.

[2] 陳劍，史韋意，蔣豐鑫，等.考慮車內振動的動力總成懸置系統多目標優化[J].中國機械工程,2015,26(8)：1129-1135. CHEN Jian，SHI Weiyi, JIANG Fengxin， et al. Multi-objective Optimization of the Powertrain Mounting System Concurrently Considering Energy Decoupling and Vehicle Vibration[J]. China Mechanical Engineering,2015，26(8)：1129-1135.

[3] 徐石安.汽車發動機彈性支承隔振的解耦方法[J].汽車工程.1995，17(4):198-204. XU Shi’an. Vibration Isolation and Decoupling Technique of Engine-mount on Vehicles[J].Automotive Engineering,1995，17(4):198-204.

[4] 沈忠亮.汽車發動機懸置系統隔振技術研究[D].合肥:合肥工業大學,2015. SHEN Zhongliang. Research on the Vibration Isolation Technology of Automotive Engine Mount System[D].Hefei: University of Technology,2015.

[5] 吳杰，周勝男. 動力總成懸置系統頻率和解耦率的穩健優化方法[J].振動與沖擊,2012,31(4)：1-7. WU Jie，ZHOU Shengnan. Robustness Optimization Method for Frequency and Decoupling Ratio of Powertrain Mounting Systems[J]. Journal of Vibration and Shock,2012,31(4)：1-7.

[6] 吳杰，劉玉波.動力總成懸置系統頻率和解耦率的區間分析方法[J].噪聲與振動控制,2012,6(3):12-15.WU Jie，LIU Yubo. Interval Analysis for Intrinsic Frequency and Decoupling Ratio of Powertrain Mounting Systems[J]. Noise and Vibration Control,2012,6(3):12-15.

[7] 邱志平，王靖.不確定參數結構特征值問題的概率統計方法和區間分析方法的比較[J].航空學報,2007,28(3):590-592. QIU Zhiping，WANG Jin. Comparison of Probabilistic Statistical Method and Interval Analysis Method for Eigenvalue Problem of Structure System with Uncertain Parameters[J]. Acta Aeronautica et Astronautica Sinica,2007,28(3):590-592.

[8] QIU Z P，WANG X J. Comparison of Dynamic Response of Structures with Uncertain-but-bounded Parameters Using Non-probabilistic Interval Analysis Method and Probabilistic Approach[J]. International Journal of Solids and Structures,2003,40(20):5423-5439.

[9] WU J L，LUO Z, ZHANG Y Q，et al. Interval Uncertain Method for Multibody Mechanical Systems Using Chebyshev Inclusion Functions[J].Int.J. Numer.Meth. Engrg.,2013,95(7):608-630.

[10] 吳景錸.基于Chebyshev多項式的動力學不確定性區間算法研究[D].武漢：華中科技大學,2013. WU Jinglai. Dynamics Uncertainty Research Based on Interval Arithmetic Using Chebyshev Polynomials[D]. Wuhan: Huazhong University of Science and Technology,2013.

[11] JIANG C，HAN X，LIU G R，et al．A Nonlinear Interval Number Programming Method for Uncertain Optimization Problems[J]. European Journal of Operational Research,2008,188(1):1-13.

[12] 蔣爾雄，趙風光，蘇仰鋒．數值逼近[M].上海：復旦大學出版社,2008. JIANG Erxiong，ZHAO Fengguang，SU Yangfeng. Numerical Approximation[M]. Shanghai：Fudan University Press,2008.

[13] 陳國良，王煦法.遺傳算法及其應用[M].北京：人民郵電出版社,2001. CHEN Guoliang, WANG Xufa. Genetic Algorithm and Its Application[M]. Beijing: Posts and Telecom Press,2001.