結合VMD和Volterra預測模型的軸承振動信號特征提取

張云強， 張培林， 王懷光， 楊玉棟， 吳定海

(1. 軍械工程學院 車輛與電氣工程系，石家莊 050003； 2. 武漢軍械士官學校 四系，武漢 430075)

滾動軸承是旋轉機械中常見的精密零件之一，也是經常損壞的元件之一。研究表明，在使用滾動軸承的旋轉機械中，約30%的機械故障是由滾動軸承發生故障直接或間接引起的，給工業生產和生活造成巨大經濟損失[1-2]。因此，開展滾動軸承狀態識別與故障診斷意義重大。當軸承出現故障時，其振動信號具有明顯的非線性和非平穩性，蘊含著大量的軸承故障信息。如何從這些信號中提取有效特征參數是軸承故障診斷亟待解決的問題。

軸承振動信號本質是與軸承健康狀態相關的時間序列。時間序列的參數化建模可以根據系統動態數據建立準確反映數據所蘊含動態關系的數學模型，從而揭示系統結構和規律。其中自回歸(Auto Regressive，AR)模型和自回歸滑動平均(Auto Regressive and Moving Average Model，ARMA)模型是應用最廣泛的兩個時間序列模型。趙聯春等[3]對軸承振動信號信號分析中的AR模型進行了深入研究；孫學斌[4]利用AR模型對機床軸承振動信號進行建模，從而實現了軸承故障診斷；劉穎等[5]結合ARMA模型和聚類分析提取了軸承振動信號特征參數，達到了軸承故障類型的準確識別的目的。雖然AR模型和ARMA模型在軸承故障診斷中取得了較好的效果，但是二者均是線性預測模型，在對時間序列建模時，常常假設信號是平穩的，導致在處理非線性和非平穩的軸承故障信號時容易產生較大的誤差，從而影響軸承故障診斷精度[6-7]。

為了解決上述問題，一些學者引入經驗模態分解(Empirical Mode Decomposition, EMD)[8]和Volterra預測模型。EMD能夠依據信號本身的特性，將非平穩信號分解為若干個平穩的本征模式函數(Intrinsic Mode Function, IMF)分量。Volterra模型是一種非線性預測模型，廣泛應用于工程中的非線性系統建模。Cheng等[9-10]提出了一種基于EMD和AR模型的滾動軸承故障診斷方法，緩解了AR模型在非平穩信號建模中的不足；陳冬青等[11]結合ARMA模型與EMD提取了軸承振動信號的關聯維數，提高了軸承損傷評定精度；Tang等[12]深入研究了Volterra模型在軸承故障診斷中的應用，取得了比AR模型更好的效果；裘焱等[13]在EMD分解的基礎上對各分量建立Volterra模型，實現了非線性和非平穩信號的故障特征提取。然而，EMD缺乏嚴格的數學基礎，對信號中的噪聲比較敏感，容易產生嚴重的頻率混疊現象，給軸承故障特征提取帶來新的問題。

變分模式分解(Variational Mode Decomposition, VMD)[14]是一種新的自適應時頻分析理論。與EMD相比，該理論采用完全非遞歸的方式實現信號的頻域分解，具有分解能力強、抗噪性能好和處理速度快等特點[15-17]。因此，本文提出一種結合VMD和Volterra預測模型的滑動軸承振動信號特征提取方法，利用VMD將軸承振動信號分解成有限個平穩的IMF分量，在重構相空間內對各IMF分量采用Volterra預測模型進行非線性建模，并通過類內類間距準則對模型參數進行優選，用于準確描述軸承故障信號的非線性和非平穩性特征。

1 變分模式分解

1.1 變分模式分解理論

變分模式分解是建立在Wiener濾波、希爾伯特變換、解析信號、頻率混合和外差解調等概念基礎上的一種新的自適應時頻分析方法，具有嚴格的數學基礎，其分解過程本質上是一個特殊變分模型的迭代求解過程。

在建立信號分解的變分模型之前，VMD理論摒棄了EMD理論中IMF的定義，而將IMF進行了重新定義，即信號的IMF分量均是調幅-調頻信號，如式(1)所示。

uk(t)=Ak(t)cos(φk(t))

(1)

式中：uk(t)為第k個IMF分量；Ak(t)和φk(t)分別為uk(t)的瞬時幅值和相位;φk(t)為非減函數，即瞬時頻率ωk(t)=dφk(t)/dt≥0。與φk(t)相比，Ak(t)和ωk(t)的變化比較緩慢，即在較短的時間范圍內可以認為是幅值和頻率不變的諧波信號。

在上述定義基礎上，VMD理論假設輸入信號信號x(t)是由有限個帶寬有限、中心頻率不同的IMF組成，在各IMF分量之和等于輸入信號x(t)的約束下，以尋求每個本征模態函數分量的估計帶寬之和最小為目標構建信號分解的變分模型。變分模型的建立過程如下：

(1) 希爾伯特變換。對每個IMF分量進行希爾伯特變換，并為獲得uk(t)的單邊頻譜，構造解析信號

*uk(t)

(2)

(2) 頻率混合。給各IMF分量的解析信號混合一個預先估計的中心頻率e-jωkt，從而將每個IMF分量的頻譜移動到基頻帶上，即

(3)

(3) 帶寬估計。通過計算式(3)所示解調信號梯度的L2范數，估計各IMF分量的帶寬。

(4) 建立最優化模型。引入約束條件，構建如下最優化變分模型

(4)

式中：K為IMF分量個數；{uk}={u1,u2,…,uK}，{ωk}={ω1,ω2,…,ωK}表示uk的頻率中心。

為了對上述變分模型進行求解，VMD首先引入二次懲罰因子α和拉格朗日乘子λ(t)，構造式(5)所示的擴展拉格朗日函數L({uk},{ωk},λ)，將約束問題轉化為非約束問題。其中α可以在含高斯噪聲的情況下保證信號的重構精度，λ(t)可以確保模型約束條件的嚴格性。然后，利用乘法算子交替方向法(Alternating Direction Method of Multipliers，ADMM)，交替迭代更新{uk}、{ωk}和λ，搜索擴展拉格朗日函數的鞍點，即為式(4)所示變分模型的最優解，從而將輸入信號x(t)分解為K個帶寬有限的IMF分量。變分模型的具體求解流程如圖1所示。初始化時，{uk}、{ωk}和λ均取值為0。

L({uk},{ωk},λ)=

(5)

1.2 仿真信號分析

為了分析變分模式分解的信號分解能力，構造仿真信號x(t)，如式(6)所示。

x(t)=x1(t)+x2(t)+x3(t)+sn(t)

(6)

式中：x1(t)、x2(t)和x3(t)分別為頻率為10 Hz、50 Hz和75 Hz的正弦諧波信號，x1(t)和x3(t)的幅值為1，x2(t)的幅值為1.5；sn(t)為幅值為0.05的隨機白噪聲。設置信號的采樣頻率為4 096 Hz，采樣時間為0.5 s，則仿真信號x(t)及其各分量的時域波形如圖2所示。

圖1 變分模型求解流程圖

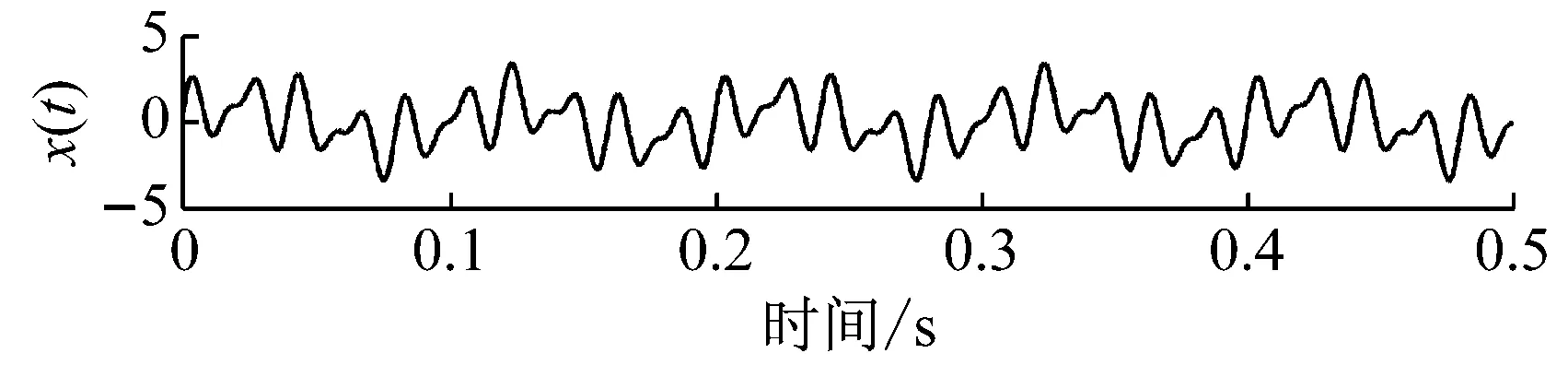
圖2 仿真信號及其各分量時域波形

圖3為仿真信號的EMD分解結果。由圖3可知，EMD將仿真信號分解成7個IMF分量和1個殘余分量。其中，IMF1分量主要是隨機白噪聲；IMF5與10 Hz正弦諧波分量有較好的對應關系；IMF2和IMF3分量雖然與50 Hz和75 Hz兩個正弦諧波分量對應，但是EMD無法將兩個正弦諧波分量進行有效分離，產生了嚴重的頻率混疊現象，并且受噪聲干擾，波形也出現了明顯失真；IMF4、IMF6、IMF7和R4個分量與仿真信號沒有較好的對應關系，是信號分解時產生的虛假分量。

圖3 仿真信號EMD分解結果

選擇K=4，α=2 000，采用VMD對仿真信號x(t)進行分解，結果如圖4所示。由圖4可知，VMD能準確地把仿真信號的3個正弦諧波分量和1隨機白噪聲分量很好地分離開，其中IMF1、IMF2和IMF3分別與正弦諧波分量x1(t)、x2(t)和x3(t)對應，IMF4與隨機白噪聲分量對應。

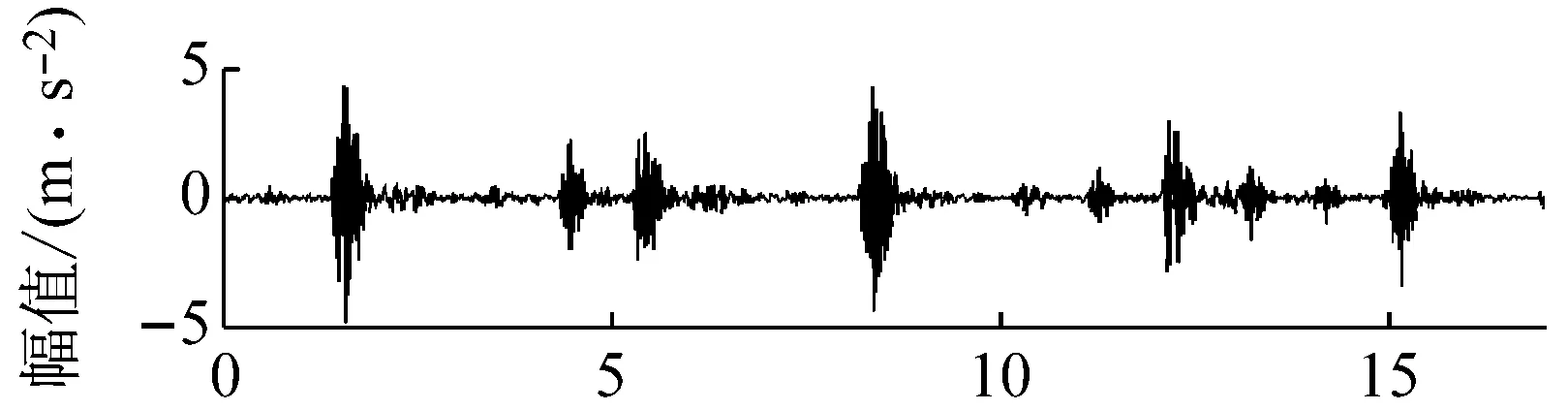
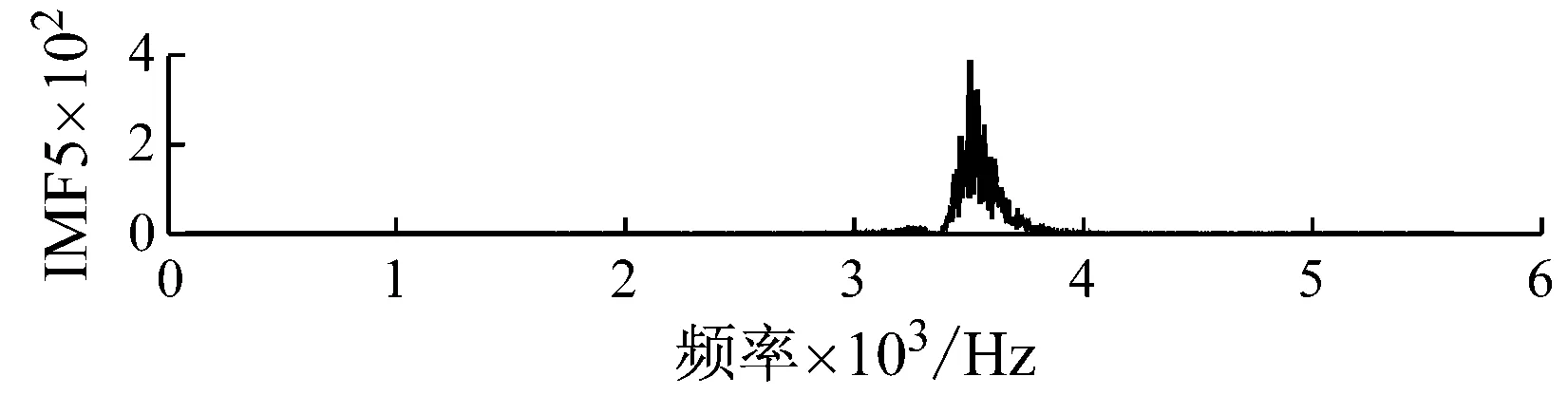
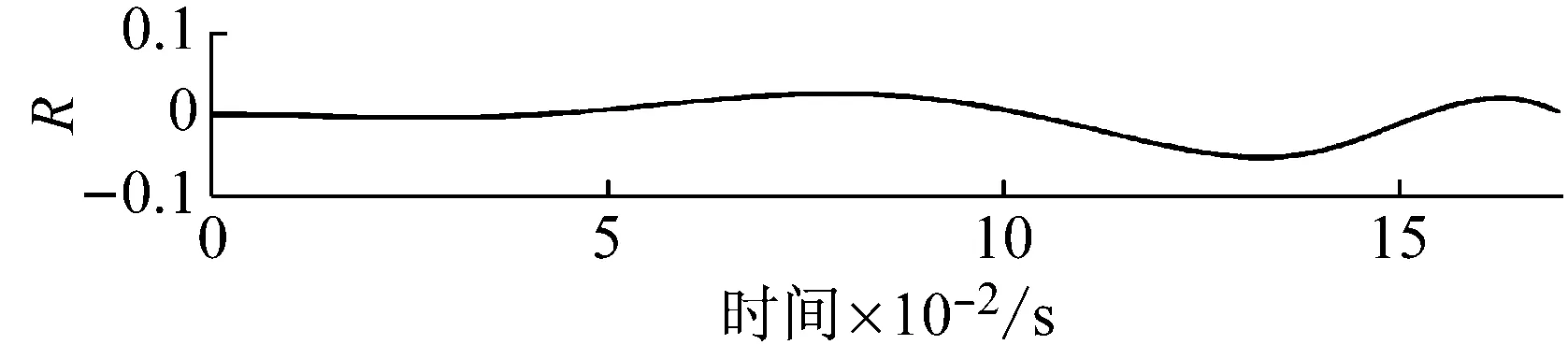
對比EMD和VMD分解結果可知，由于EMD的抗噪性能較差，且對頻率滿足f1

圖4 仿真信號VMD分解結果

2 基于相空間重構的Volterra預測模型

2.1 相空間重構

相空間重構是建立Volterra預測模型的基礎。對于一個單輸入單輸出的非線性離散系統，假設系統的輸入為時間序列x(1),x(2),…,x(n)，可以采用Takens等提出的延遲坐標法對系統進行相空間重構[18]。該重構相空間中的點可以描述為

X(n)=[x(n),x(n-τ),…,x(n-(m-1)τ)]

(7)

式中：m和τ分別為系統嵌入維數和時間延遲。

Takens定理表明，若系統嵌入維數m≥2d+1，d為系統的動力學維數，則相空間重構的系統與原系統在拓撲意義上是等價的，2個相空間中的混沌吸引子具有微分同胚的性質。因此，利用相空間重構理論和非線性系統的當前狀態，可以預測系統下一時刻的狀態，這為時間序列預測提供了理論基礎。

系統嵌入維數和時間延遲參數的估計是相空間重構的關鍵。目前，可同時估計該兩個參數的方法有C-C方法和時間窗口法等。C-C方法具有計算簡單、估計準確和抗噪性能好等優點，因此本文在相空間重構時采用C-C方法估計系統的嵌入維數m和時間延遲參數τ。

2.2 時間序列的Volterra預測模型

時間序列預測本質上是一個動力系統的逆問題，即根據動力系統的狀態構建系統的動力學模型F

y(n)=x(n+T)=F(X(n))

(8)

式中：T>0為向前預測步長。

Volterra模型是一種非線性預測模型，能夠很好地逼近模型F，廣泛應用于工程中的非線性系統建模。若非線性系統的輸入為X(n)、輸出為y(n)，則該系統的Volterra級數展開式為

(9)

式中：hk(i1,i2,…,ik)為k階Volterra核；p為級數的階數；M為記憶長度。Volterra級數屬于無窮級數，實際應用比較困難。由于工程上大部分非線性系統都可用二階的Volterra級數來描述[19]，本文選擇二階的Volterra級數構建時間序列預測模型，即

(10)

令W(n)=[h0,h1(0),h1(1),…,h1(M-1),h2(0,0),h2(0,1),…,h2(M-1,M-1)]T，Z(n)=[1,x(n),x(n-τ),…,x(n-(M-1)τ),x2(n),x(n)x(n-τ),…,x2(n-(M-1)τ)]T，則式(10)可以改寫為

y(n)=ZT(n)W(n)

(11)

利用歸一化最小均方自適應算法對式(11)進行求解，即獲得時間序列的Volterra預測模型，實現對模型F的非線性逼近。模型參數向量W(n)蘊含著系統狀態的重要信息，是系統故障診斷的重要依據。

3 結合VMD和Volterra預測模型的特征取方法

采用VMD對滾動軸承振動信號進行分解后，每個IMF分量代表著軸承信號不同頻率成分，信號的特征完全可以由K個IMF分量來描述。Volterra預測模型如同一個信息凝聚器，采用該模型對各IMF分量進行非線性建模，可將IMF分量蘊含的信息都凝聚于模型參數向量中。因此，通過對K個IMF分量的Volterra模型參數向量進行優選，就可以獲得用于描述軸承振動信號非線性和非平穩特性的特征參數。

結合VMD和Volterra預測模型的特征取方法實現步驟如下：

步驟1利用最大相關最小冗余準則[20]自動選取VMD中的參數K，然后對每一個軸承振動信號x(t)進行VMD自適應分解，得到K個IMF分量uk(t)；

步驟2采用C-C方法估計各IMF分量uk(t)的嵌入維數m和時間延遲參數τ，并對uk(t)進行相空間重構；

步驟3選取記憶長度M=m，在重構相空間中對uk(t)建立二階Volterra自適應預測模型；

步驟4依據式(12)所示的類內類間距準則對模型參數進行優選，Jb越大表明對應模型參數的區分性能越好，從而得到描述軸承振動信號的特征參數。

(12)

式中：Sb和Sw分別為類內散度和類間散度。

4 滾動軸承振動信號分析

4.1 實驗數據描述

實驗所用的滾動軸承振動信號采自于一個單級傳動齒輪箱振動試驗系統。該系統主要由臺架基座、調速電機、單級傳動齒輪箱、磁粉阻尼器、聯軸器、振動傳感器和數據采集設備等組成。采用的傳感器型號為B&K4508振動加速度傳感器，安裝在測試軸承座正上方的箱體表面。測試軸承為SKF6205深溝球軸承，安裝在調速電機輸出軸上，試驗采用電火花加工的方式分別于測試軸承的外圈、內圈和滾動體上加工深度為0.053 mm的凹槽來模擬軸承的3種常見的單點故障。試驗載荷為2.2 kW，采樣頻率為12 kHz。圖5為采集的4種不同狀態的軸承振動信號。

4.2 軸承振動信號的VMD分解

以軸承外圈故障信號為例進行分析。根據最大相關最小冗余準則，選取K=5，對圖5中軸承外圈信號進行VMD分解。

(a) 正常

(b) 外圈故障

(c) 內圈故障

(d) 滾動體故障

圖6和圖7分別展示了VMD分解結果的時域波形和頻譜。觀察圖6和圖7可知，VMD將軸承外圈故障信號分解成了5個不同頻率成分IMF分量，各分量相互獨立，不存在模態混疊的現象。

圖6 VMD分解結果時域波形

圖7 VMD分解結果的頻譜

作為對比，圖8給出了軸承外圈故障信號的EMD分解結果。由圖8可以看出，EMD將外圈故障信號分解成了7個IMF分量和1個殘余分量。IMF2與IMF3、IMF4與IMF5均存明顯的頻率混疊現象；IMF6、IMF7和R3個分量與原信號聯系較小，是分解出的虛假分量。

與VMD分解結果相比，EMD的分解結果較差，VMD具有較好的軸承信號分解能力，更加適合于軸承振動信號分解。

4.3 Volterra模型特征提取

選擇記憶長度M=m=3，對所有軸承振動信號的IMF分量在重構的相空間中建立二階Volterra自適應預測模型。由于二階Volterra自適應預測模型的參數向量W(n)有10個元素，每一個軸承振動信號會產生10×5=50個模型參數。為引入對比，對各軸承振動信號EMD分解結果的前5個IMF分量也建立二階Volterra自適應預測模型。

圖8 EMD分解結果時域波形

圖9為類內類間距準則函數Jb由大到小隨模型參數的變化情況。對比VMD與EMD對應的兩條曲線可知，除前3個和后9個模型參數的區分性能相當以外，VMD的中間38個模型參數的區分性能優于EMD。此外，VMD對應的曲線中Jb>0.9的有11個參數，而EMD僅有5個。由此說明，不同模型特征參數具有不同的軸承狀態區分能力，采用VMD分解得到的模型參數的區分性能明顯優于EMD。

取Jb>0.9，對經VMD分解得到Volterra模型參數進行選擇，最終提取出的Volterra模型特征如表1所示，表中每種軸承狀態包含2個樣本，模型參數符號上標代表IMF分量序號。觀察圖9可知，所提特征參數具有很好的類內聚合性和類間分散性，為軸承故障準確診斷奠定了良好基礎。

圖9 模型特征參數性能比較

模型參數h51(1)h31(1)h51(0)h41(0)h41(2)h51(2)h11(1)h21(0)h21(2)h21(0)h31(2)正常外圈故障內圈故障滾動體故障-0.78693.3512-2.4403-0.0121-0.69191.06230.2144-0.48880.25480.13341.4935-0.78633.1072-2.7276-0.0169-0.69491.05670.2168-0.48730.2625-0.08061.4952-1.4955-0.8800-0.0979-0.2016-0.57380.41520.0281-0.69850.1103-0.41531.3393-1.4913-0.8755-0.1047-0.2124-0.57370.42130.0241-0.69950.1105-0.42881.3430-0.59330.34240.0072-0.0755-0.58470.25790.0279-0.78480.0451-0.11221.3562-0.59540.34660.0114-0.0647-0.58710.23460.0203-0.80800.0525-0.04391.3590-1.0167-0.7608-0.1015-0.0521-0.53090.54210.2311-0.52910.06420.03231.2805-1.0242-0.7234-0.0845-0.0562-0.53110.53820.2379-0.52670.04800.08951.2657

4.4 軸承故障診斷效果

為測試所提特征參數在滾動軸承故障診斷中的效果，從4種狀態的滾動軸承信號中分別隨機選取20個樣本構造訓練集，剩余20個樣本構造測試集，采用K近鄰分類器(K-Nearest Neighbor Classifier，K-NNC)、樸素貝葉斯分類器(Naive Bayes Classifier，NBC)和支持向量機(Support Vector Machine，SVM)分別對滾動軸承振動信號進行分類。在K-NNC分類時，取K=1；在SVC分類時，采用徑向基核函數和“一對一”策略構建多類分類器，并通過交叉驗證的方法自動選擇參數。同時，選取經EMD分解的Volterra模型參數中Jb>0.9的特征參數構造對比實驗。為了降低實驗結果的隨機性，實驗重復5次，每次參與實驗的樣本均重新隨機選取。表2給出了5次實驗的平均分類結果。

表2 滾動軸承振動信號分類結果

由表2可以看出，采用不同分類器進行分類時，結合VMD分解提取的模型參數的分類精度達最高達到98.00%，最低達到95.25%，而結合EMD分解提取的模型參數的分類精度最高分類精度僅為93.00%；就相同分類器而言，結合VMD分解提取的模型參數的分類效果均優于結合EMD分解提取的模型參數。分類結果表明，與EMD相比，結合VMD提取的Volterra模型特征能更準確地對滾動軸承故障進行診斷。

5 結 論

針對非線性、非平穩的滾動軸承振動信號，提出了一種結合變分模式分解和Volterra預測模型的滾動軸承振動信號特征提取方法。該方法利用變分模式分解將軸承振動信號自適應地分解為有限個平穩的IMF分量，進而對各IMF分量建立Volterra自適應預測模型，采用類內類間距準則對模型參數進行優選，從而提取振動信號的Volterra模型參數。實驗結果表明，結合變分模式分解提取的Volterra模型特征能有效表達振動信號的非線性和非平穩特性，從而提高滾動軸承故障診斷精度。

[1] 徐振輝, 馬立元. 滾動軸承的故障特征提取[J]. 兵工自動化, 2004, 23(1): 46-48.

XU Zhenhui, MA Liyuan. Picking up fault character of rolling bearings[J]. Ordnance Industry Automation, 2004, 23(1): 46-48.

[2] 王宏超, 陳進, 董廣明. 基于最小熵解卷積與稀疏分解的滾動軸承微弱故障特征提取[J]. 機械工程學報, 2013, 49(1): 88-94.

WANG Hongchao, CHEN Jin, DONG Guangming. Fault diagnosis method for rolling bearing’s weak fault based on minimum entropy deconvolution and sparse decomposition[J]. Journal of Aechanical Engineering, 2013, 49(1): 88-94.

[3] 趙聯春, 馬家駒, 范樹遷，等. 滾動軸承振動分析中的AR模型研究[J]. 中國機械工程, 2004, 15(3): 210-213.

ZHAO Lianchun, MA Jiaju, FAN Shuqian, et al. Research on AR model in vibration analysis of rolling bearing[J]. China Mechanical Engineering, 2004, 15(3): 210-213.

[4] 孫學斌. AR模型和SVM在機床滾動軸承故障診斷中的應用[J]. 機械工程與自動化, 2010, 44(2): 132-134.

SUN Xuebin. Application of AR model and SVM in machine rolling bearing fault diagnosis[J]. Mechanical Engineering & Automation, 2010, 44(2): 132-134.

[5] 劉穎, 嚴軍. 基于時間序列ARMA模型的振動故障預測[J]. 化工自動化及儀表, 2011, 38(7): 841-843.

LIU Ying, YAN Jun. Vibration faults prediction based on time series auto regressive moving average(ARMA) model[J]. Control and Instruments in Chinese Industry, 2011, 38(7): 841-843.

[6] 范庚, 馬登武. 基于EMD和RVM-AR的航空發動機磨損故障預測模型[J]. 計算機測量與控制, 2013, 21(3): 1746-1749.

FAN Geng, MA Dengwu. Aero-engine wear faults prediction based on EMD and RVM-AR[J]. Computer Measurement & Control, 2013, 21(3): 1746-1749.

[7] 王儼剴, 馬進銳, 廖明夫，等. 發動機振動趨勢預測模型研究[J]. 振動、測試與診斷, 2014, 34(3): 517-523.

WANG Yankai, MA Jinrui, LIAO Mingfu, et al. Research on trend prediction model of engine vibration[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(3): 517-523.

[8] HUANG N E, SHEN Z, LONG S R, et al. The empirical model decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Processing of Royal Society of London A, 1998, 454: 903-995.

[9] CHENG Junsheng, YU Dejie, YANG Yu. A fault diagnosis approach for roller bearings based on EMD method and AR model[J]. Mechanical System and Signal Processing, 2006, 20(2): 350-362.

[10] 孟宗, 顧海燕. 應用經驗模態分解下的AR模型提取旋轉機械故障特征[J]. 燕山大學學報, 2011, 35(4): 342-326.

MENG Zong, GU Haiyan. Research on fault feature extraction of rotating machine based on empirical mode decomposition and AR model[J]. Journal of Yanshan University, 2011, 35(4): 342-326.

[11] 陳冬青, 許紅波, 王新華. 基于ARMA模型關聯維數與LSSVM的軸承損傷評定[J]. 起重運輸機械, 2015(5): 51-55.

CHEN Dongqing, XU Hongbo, WANG Xinhua. Bearing damage assessment based on the correlation dimension of ARMA model and LSSVM[J]. Hoisting and Conveying Machinery, 2015(5): 51-55.

[12] TANG H, LIAO Y H, CAO J Y，et al. Fault diagnosis approach based on Volterra model[J]. Mechanical System and Signal Processing, 2010,24(4): 1099-1113.

[13] 裘焱, 吳亞峰, 李野. 應用EMD分解下的Volterra模型提取機械故障特征[J]. 振動與沖擊, 2010, 29(6): 59-61.

QIU Yan, WU Yafeng, LI Ye. Applying EMD decomposition of the Volterra model to extract mechanical fault feature[J]. Journal of Vibration and Shock, 2010, 29(6): 59-61.

[14] KONSTANTIN D, DOMINIQUE Z. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.

[15] SALIM L. Comparative study of signal denoising by wavelet threshold in empirical and variational mode decomposition domains[J]. Healthcare Technology Letters, 2014,1 (3): 104-109.

[16] WANG Yanxue, RICHARD M, XIANG Jiawei, et al. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system[J]. Mechanical Systems and Signal Processing, 2015, 60/61: 243-251.

[17] ANEESH C, SACHIN K, HISHAM P M, et al. Performance comparison of variational mode decomposition over empirical wavelet transform for the classification of power quality disturbances using support vector machine[J]. Procedia Computer Science, 2015, 46: 372-380.

[18] 韓敏. 混沌時間序列預測理論與方法[M]. 北京:中國水利水電出版社, 2007.

[19] CHOW T W S, TAN H Z. HOS-based nonparametric and parametric methodologies for machine fault detection[J]. IEEE Transactions on Industrial Electronics, 2000, 47(5): 1051-1059.

[20] PENG H C, LONG F H, CHRIS D. Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(8): 1226-1238.