含預制孔容器內爆問題的FEM-SPH耦合算法模擬

胡廷勛， 胡德安

(湖南大學 特種裝備先進設計技術與仿真教育部重點實驗室， 長沙 410082)

抗爆容器通常是指一定的爆炸物在其內部爆炸時，對周圍環境不造成損壞和污染的一種密封抗壓容器。在軍事、科研、工業以及環保等領域都有應用[1]，一般用于爆轟及爆炸效應的試驗研究，也可作為某種特殊要求的安全防護構件。

內爆容器實驗研究成本昂貴，對實驗環境和測試技術要求高，且受測試技術限制，所測實驗數據極為有限。相比較于實驗研究，數值計算能夠更好地研究抗爆容器內部爆炸載荷的特征和分布規律。光滑粒子流體動力學(Smoothed Particle Hydrodynamics, SPH)方法作為一種具有無網格性質和拉格朗日性質的粒子法，能夠很自然的捕獲研究對象的運動歷程，并且可以很容易地描繪出物質交界面、自由表面以及運動交界面等[2]。SPH方法的無網格特性也使得該方法可以在拉格朗日框架內處理大變形問題，克服計算中大變形相關問題，故適宜采用SPH方法對高能炸藥爆炸過程進行模擬分析。但是在小變形動力學問題中，SPH方法的精度和效率總體上沒有有限元(Finite Element Method, FEM)方法理想。因此，一個合理的方法就是在大變形區域應用SPH算法，在小變形區域應用傳統有限元方法進行模擬分析[3]。

FEM-SPH自適應耦合算法根據等效塑性應變自動將畸變FEM單元轉化為SPH粒子，既能避免單元畸變，又能減少了SPH計算區域，已成功應用到爆炸、沖擊等問題的數值模擬中[4-6]。王吉等同時采用FEM算法、SPH算法和FEM-SPH自適應耦合算法模擬Taylor碰撞問題，結果顯示自適應耦合算法的結果更趨近于光滑粒子法，即畸變單元轉化為SPH粒子對模擬結果影響較小，無傳統FEM侵蝕算法刪除單元產生的誤差。因此，在FEM-SPH自適應耦合算法中，可以充分發揮SPH算法模擬大變形問題無單元畸變和FEM算法模擬小變形問題效率高的特點和優勢。

目前，對容器內爆問題的模擬主要采用有限差分法、有限體積法、任意拉格朗日歐拉(Arbitrary Lagrange-Euler, ALE)方法[7-9]等開展研究。基于歐拉格式的數值方法需要補充額外的算法追蹤界面，并且界面追蹤的精度要求越高，計算所需的時間越多。應用FEM-SPH自適應耦合算法對容器內爆問題的模擬可自然的追蹤移動界面，但相關研究還比較缺乏。本文結合相關實驗，采用FEM-SPH自適應耦合算法模擬含預制孔容器在內爆載荷作用下的動態響應，同時也用LS-DYNA軟件中的ALE算法得到的計算結果進行比較分析，研究FEM-SPH自適應耦合算法模擬內爆問題的適用性，為內爆容器問題數值模擬研究提供有效途徑。

1 FEM-SPH自適應耦合算法

1.1 基本方程

將人工黏度和人工熱量考慮在內的SPH離散格式表示的Navier-Stokes方程組可寫為[10]

(1)

式中：m為質量;ρ為密度;e為內能;να為速度分量;σαβ為總應力張量;xα為空間坐標;t為時間;p為各向同性壓力;εαβ為黏性剪切應力;∏ij為人工黏度;Hi為人工熱量;W為光滑函數。光滑函數選取三維空間的二次光滑函數，即

0 ≤R≤ 2

(2)

式中：h為光滑長度。R=r/h，r為兩點間的距離。SPH方法在模擬炸藥爆炸和容器內空氣時總應力張量只考慮壓力作用，而在模擬容器時需考慮黏性剪切應力項。

FEM相關理論已經發展的很成熟，FEM模擬爆炸沖擊問題的基本方程詳見文獻[11]。

1.2 FEM-SPH自適應耦合算法

文中FEM-SPH自適應耦合算法采用三維四面體單元對含預制孔容器、炸藥及空氣進行初始離散，計算過程中，以材料的等效塑性應變為判據，當表征材料的有限單元等效塑性應變達到預設值時，單元自動轉換成SPH粒子。

單元轉化為粒子后，粒子的質量、速度和質心與原單元保持一致。粒子半徑d的計算公式為

(3)

式中：V為有限單元轉化成SPH粒子時的體積。

有限元四面體單元分三種情況轉化為SPH粒子，如圖1所示。單元A轉化為粒子A后，在接觸列表中刪除三角形面a-b-c和a-c-d，增加面a-b-d和b-c-d，而光滑粒子A只能固接在一個接觸面上，選擇其中面積最大面進行耦合；光滑粒子B生成以后，原接觸主面e-f-g、e-g-h和e-h-f被刪除，新增加接觸主面f-g-h，粒子B與面f-g-h耦合；單元C的四個面在轉化為粒子后則全部刪除，粒子C與節點k耦合。針對以上單元和粒子的耦合，本文采用Johnson提出的耦合算法進行處理，文獻[12]中給出了具體的耦合算法理論和公式。耦合算法用于處理同一物體內部單元與粒子的相互作用。

(a)單元轉化為粒子前(b)單元轉化為粒子后

圖1 四面體單元轉化為粒子示意圖

Fig.1 Schematic diagram of the tetrahedral elements transformed into particles

FEM-SPH自適應耦合算法中存在三種接觸，即粒子-單元、單元-單元及粒子-粒子接觸，Johnson等[13-14]提出的對稱接觸、滑移界面算法以及粒子與單元接觸算法，能較好地處理單元-單元和單元-粒子之間的接觸。Campbell等[15]提出的粒子-粒子罰接觸算法，可較好地處理粒子-粒子之間的相互作用。接觸算法用于處理不同物體之間的相互作用。

本文所建立的模型中，炸藥與空氣采用共節點單元進行初始離散，炸藥、空氣與容器之間的相互作用采用接觸算法進行計算。炸藥、空氣與容器的等效塑性應變判定值分別為0.05、0.01和0.5，能夠保證內部炸藥與空氣起爆后迅速轉化為SPH粒子。新產生的粒子在后續的計算中，相關物理量通過SPH方程計算，并引入單元-粒子耦合算法。隨著單元不斷轉化成粒子，單元區域與粒子區域不斷發生變化，在計算中會不斷更新耦合界面。

2 材料模型

數值模擬中，TNT炸藥模型采用以下本構方程[16]為

(4)

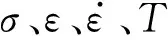
(5)

式中：Tr為室溫；Tm為熔化溫度。TNT炸藥本構方程材料常數見表1。

空氣介質在起爆后迅速轉化為SPH粒子，轉化時其體膨脹率比較小，計算時采用一般的黏性流體運動公式，即[17]

(6)

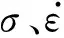
(7)

式中：E為單位體積內能；V為相對體積；C1、C2為材料常數。空氣的初始內能為0，密度取1.225 kg/m3，初始相對體積取1.0，C1=C2=0.4。

對TNT炸藥爆炸的壓力-體積-能量特征的描述采用JWL方程，即

(8)

式中：VT為比容；E0為爆炸氣體密度與初始炸藥密度的比值；e為單位質量炸藥的內能；A、B、R1、R2、ω為擬合系數。在計算中還會用到炸藥初始密度ρ0，爆轟速度D，以及Chapman-Jouget壓力PCJ。TNT炸藥JWL方程相關參數見表2。

含預制孔金屬容器采用Johnson-Cook本構模型和Mie-Gruneisen狀態方程進行描述，即

(9)

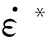
表1 TNT本構關系中的材料常數

表2 TNT炸藥JWL方程參數

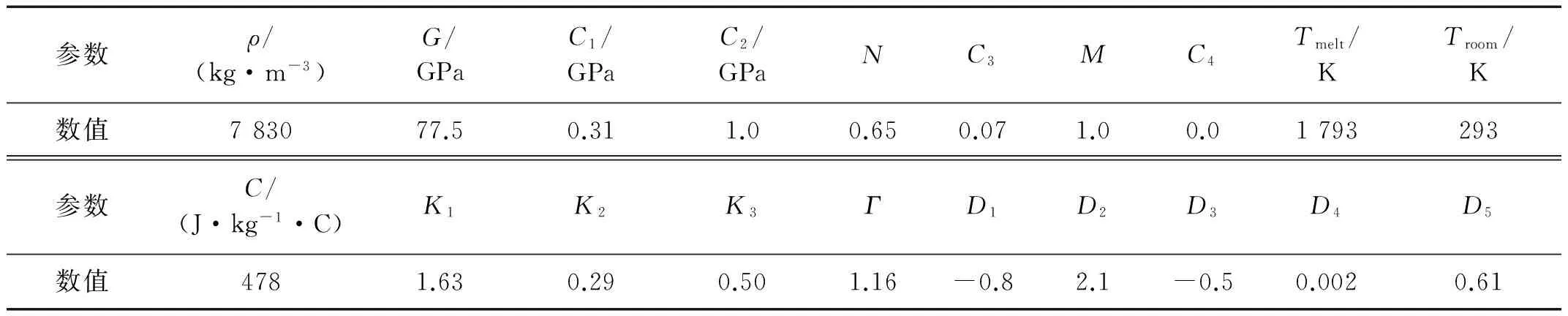
表3 金屬容器材料參數

3 數值模型及結果驗證

[7-9]中采用不同尺寸的含預制孔金屬容器進行了內爆加載實驗，實驗方案如圖2所示。本文建立了不同藥量TNT在不同厚度含預制孔容器內的爆炸模型，數值模型與相應實驗的試件尺寸、材料，預制孔形貌與位置、裝藥形狀、裝藥位置保持一致。模型中TNT炸藥為等長徑比圓柱形。由于模型的特點，采用三維實體建模。為了減小計算規模，建立1/2對稱模型。論文分別采用FEM-SPH自適應耦合算法和LS-DYNA軟件中ALE算法進行模擬，如圖3所示，ALE算法中采用流固耦合定義容器與內部爆炸流場的相互作用。數值模擬獲取爆炸過程中筒壁的Von-Mises應力圖、鼓包半徑以及預制孔變化情況。通過實驗結果、FEM-SPH自適應耦合算法結果及ALE算法結果的對比，研究FEM-SPH自適應耦合算法模擬內爆容器爆炸響應的有效性。

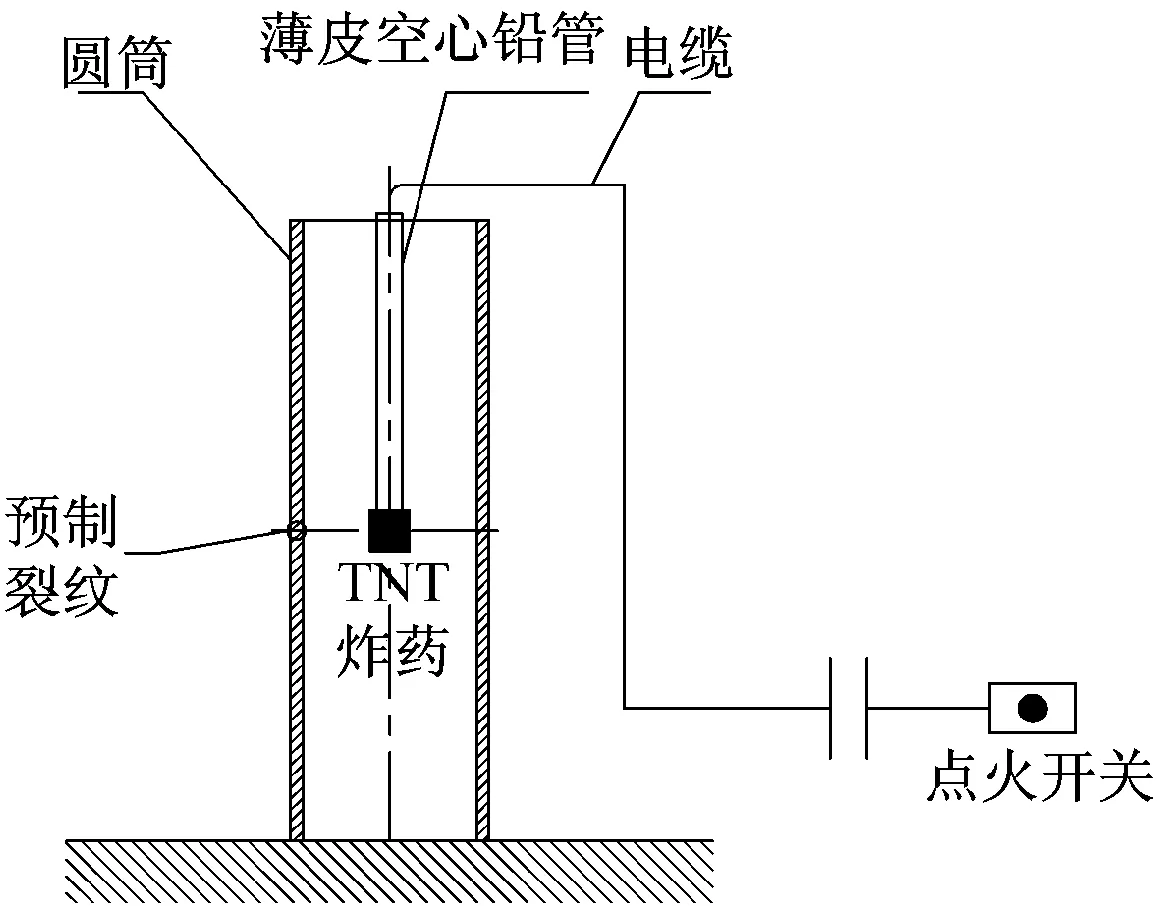
圖2 實驗裝置示意圖

為保證本文模型能夠對最終破壞形貌進行準確模擬，論文參考文獻[18]，將含預制孔容器可能破壞區域的計算網格尺寸設置小于1 mm。

(a)FEM-SPH模型(b)ALE模型

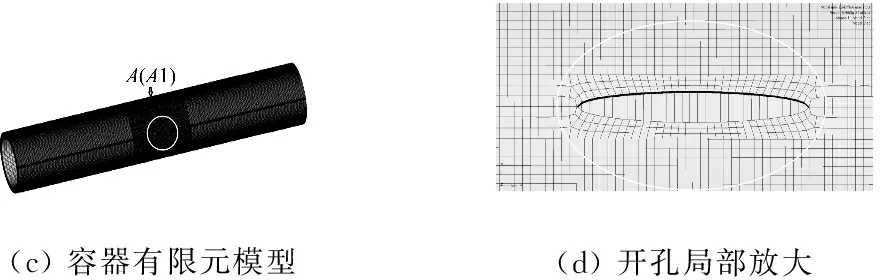
(c)容器有限元模型(d)開孔局部放大

圖3 數值計算模型

Fig.3 Numerical model

3.1 15 g TNT炸藥內爆加載下的薄壁容器

薄壁容器長度為250 mm，外徑為76 mm，厚度為3 mm。預制孔長度為5 mm，寬度為1 mm。圖4給出了實驗和FEM-SPH自適應耦合算法得到的含預制孔容器在爆炸載荷作用下的最終形貌。實驗以及數值模擬得到最終的鼓包半徑、收縮長度、預制孔寬度及長度如表4所示。另外，由于參考文獻中實驗沒有給出內爆加載下薄壁容器的動態響應過程量，論文進一步選取即有大變形又遠離預制孔應力集中區域的A點(示意圖如圖3(c)所示)的Von-Mises應力值隨時間變化曲線對比分析ALE算法與FEM-SPH自適應耦合算法。由數值模擬結果可以知道，A點應力值在50 μs左右達到最大值，故選取0～70 μs時間段進行比較研究，如圖5所示。從圖表中可以看出，采用FEM-SPH自適應耦合算法得到的結果與LS-DYNA軟件中ALE算法模擬得到的結果及實驗結果都比較吻合，定性的驗證了FEM-SPH自適應耦合算法模擬薄壁容器內爆問題的有效性。

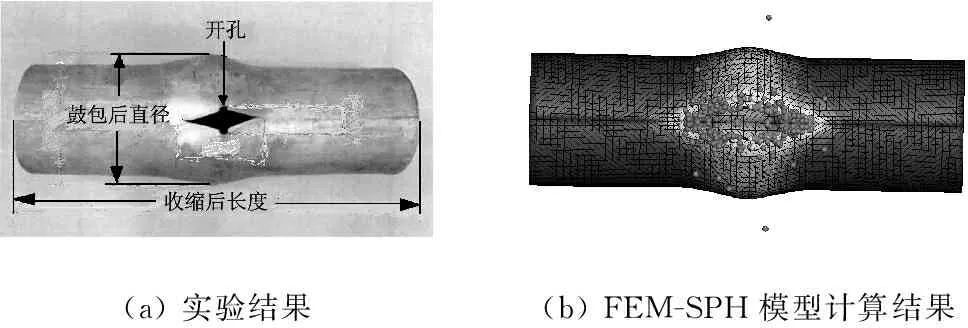
(a)實驗結果(b)FEM-SPH模型計算結果

圖4 薄壁容器實驗和數值模擬獲得的最終形貌

Fig.4 The final morphology obtained by the experiment and numerical simulation for the thin-walled vessel

圖5 A點的Von-Mises應力

3.2 600 g TNT炸藥內爆加載下的厚壁容器

厚壁容器長度為1 000 mm，外徑為93.5 mm，厚度為18.5 mm。預制孔長度為15 mm，寬度為2 mm。針對內爆載荷作用下的厚壁容器，文獻[9]研究表明預制孔裂紋會沿著絕熱剪切帶方向擴展，此時將呈現絕熱剪切為主導的韌性斷裂模式。圖6所示為實驗得到的最終形貌與FEM-SPH自適應耦合算法計算得到的結果的比較。從圖中可以看出，采用FEM-SPH自適應耦合算法模擬結果與實驗得到的孔口破壞形貌有一定差別，但基本能反應出絕熱剪切破壞。表5中進一步比較了實驗、FEM-SPH自適應耦合算法與ALE算法計算得到的鼓包半徑、收縮長度、孔口的寬度和剪切角，從表中可以看出FEM-SPH自適應耦合算法與ALE算法模擬結果具有較好的一致性，并且與實驗獲得的剪切破壞角度吻合較好。表5中數值模擬計算得到的孔端點距離與實驗結果有較大差距，這是由于含預制孔容器在內爆加載下金屬材料存在斷裂破壞，這部分理論在本構方程描述中還有待進一步完善。另外，ALE算法得到的孔口的寬度也與ALE界面追蹤算法的精度有關，兩種數值模擬方法的結果也僅是定性的比較驗證FEM-SPH模型的合理性。

(a)實驗結果(b)FEM-SPH模型計算結果

圖6 厚壁容器實驗和數值模擬獲得的最終形貌

Fig.6 The final morphology obtained by the experiment and numerical simulation for the thick-walled vessel

論文為了進一步分析FEM-SPH自適應耦合算法模擬內爆問題的有效性，選取A1點的Von-Mises應力值對FEM-SPH自適應耦合算法與ALE算法進行比較研究，A1點的位置示意如圖3(c)所示。由數值模擬結果可知，A1點Von-Mises應力值在100 μs左右達到最大值，所以選取0～120 μs時間段進行研究。圖7所示為FEM-SPH自適應耦合算法以及ALE算法得到的A1點在0～120 μs的Von-Mises應力。從圖7中可以看出，由FEM-SPH自適應耦合算法得到的A1點的Von-Mises應力值與LS-DYNA中的ALE算法得到結果吻合較好。本模型計算結果進一步闡述了FEM-SPH自適應耦合算法模擬內爆厚壁容器爆炸響應的合理性。

圖7 A1點的Von-Mises應力

表4 薄壁容器實驗及數值模擬得到的最大鼓包半徑、收縮長度、孔口寬度及長度

表5厚壁容器實驗及數值模擬得到的最大鼓包半徑、收縮長度、孔口的寬度和剪切角

Tab.5Themaximumbulgingradius,finallength,widthandshearangleoftheholeobtainedbytheexperimentandnumericalsimulationsforthethick-walledvessel

鼓包半徑/mm收縮長度/mm孔端點距離/mm剪切破壞角度/(。)實驗FEM-SPHALE111106998998110697245.042.050.4

4 容器內介質的動態響應

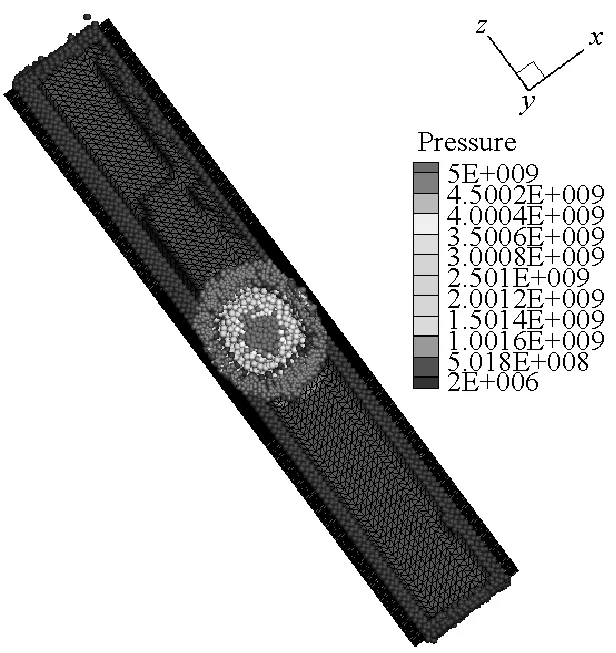
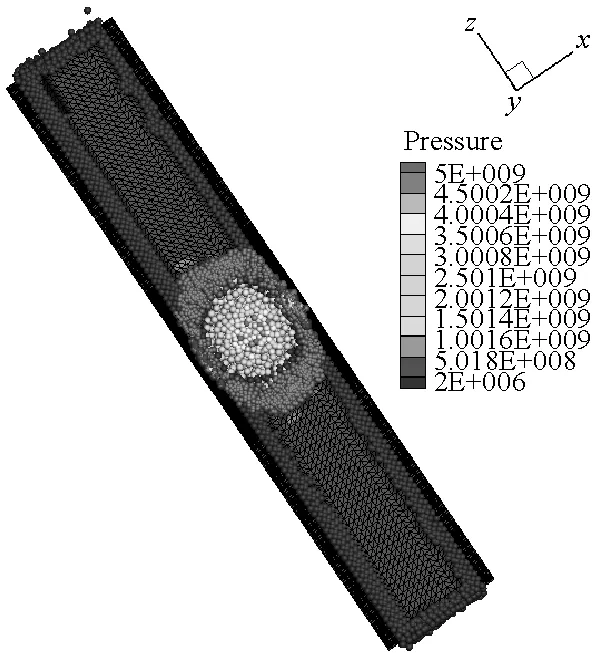
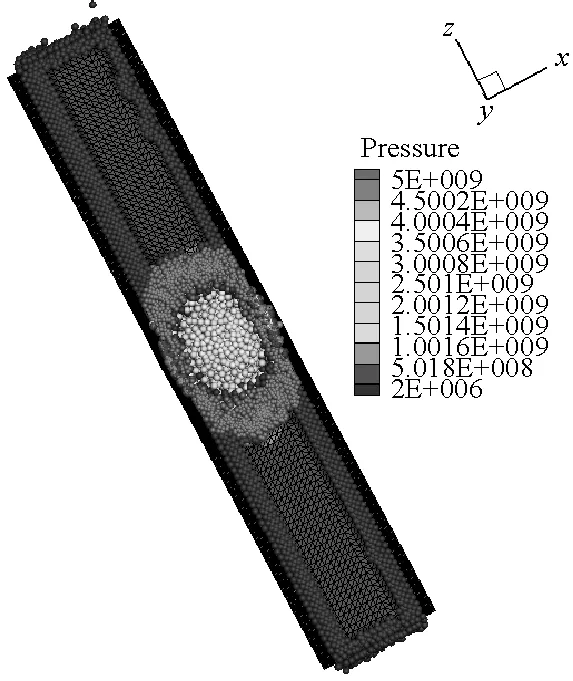
在炸藥與靶體距離較近或者嵌入靶體內部的情況下，FEM-SPH自適應耦合算法模擬爆炸問題一般都忽略炸藥周圍空氣對爆炸毀傷效應的影響。由于內爆容器的結構特點，空氣介質會對容器的爆炸毀傷效應產生顯著影響。因此，本文在前面模型計算中，考慮了空氣的影響，并且初始模型全部采用單元進行離散，充分利用FEM計算效率高的特點。計算過程中，將大變形處的單元自動轉化為SPH粒子，再利用SPH方法模擬大變形計算精度高、無網格依賴的特點進行模擬計算。圖8給出了厚壁容器內70 μs前炸藥和空氣介質的離

散分布。從圖中可以看出炸藥和空氣介質單元轉化為SPH粒子的過程，并且容器內壁處由于接觸力的作用，使得單元更先轉化為SPH粒子。

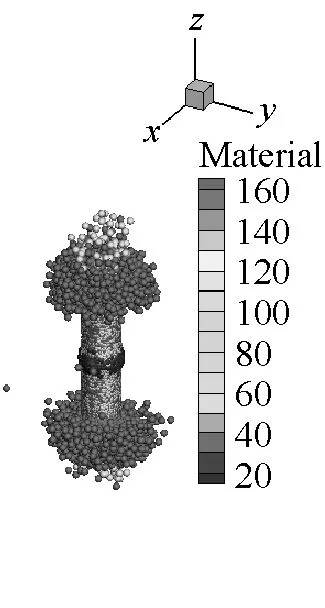
SPH方法作為一種具有無網格性質和拉格朗日性質的粒子法，研究對象的運動歷程能夠很自然地被捕獲，可以很好地描述容器內部空氣介質的爆轟變化過程，能夠更方便描述爆轟過程對于周圍環境的影響。本文薄壁容器和厚壁容器在爆炸載荷作用下內部介質的運動歷程分別如圖9和圖10所示。從圖9和圖10中可以看出，由于厚壁容器的長度是薄壁容器長度的4倍，盡管厚壁容器內的炸藥藥量增加了，但是空氣從厚壁容器的兩個端口噴出的時間還是滯后，并且模擬結果中可以明顯看到空氣粒子從容器預制孔中噴出。

圖11和12給出了薄壁容器和厚壁容器內測點的壓力曲線，圖中A2和A3點距各自炸藥中心的距離與炸藥中心到容器壁的距離一致。從圖中可以看出，TNT炸藥在空氣中形成壓力脈沖的時間為微秒級，由于厚壁容器內的炸藥藥量更大，使得其壓力脈沖峰值更高，脈沖持續時間更長。薄壁容器測點A2處的壓力峰值為220 MPa，壓力脈沖持續時間約為40 μs。厚壁容器測點A3處的壓力峰值為420 MPa，壓力脈沖持續時間約為60 μs。

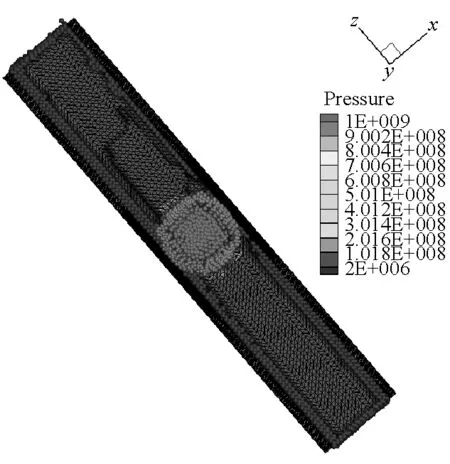
(a) t=15 μs

(b) t=20 μs

(c) t=25 μs

(d) t=30 μs

(e) t=40 μs

(a) t=20 μs

(b) t=40 μs

(c) t=60 μs

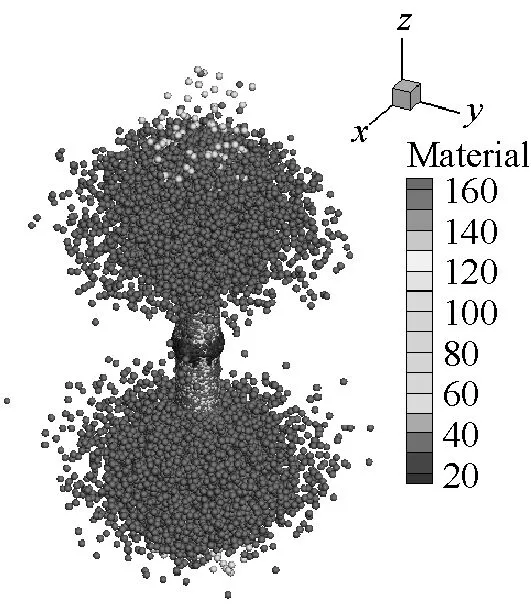
(d) t=100 μs

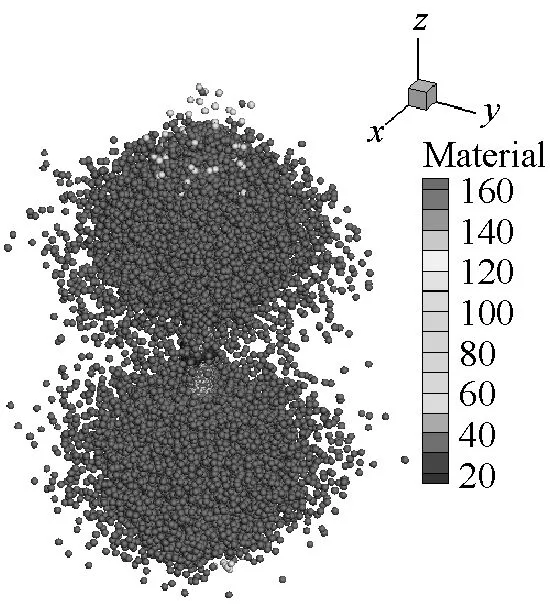
(e) t=150 μs

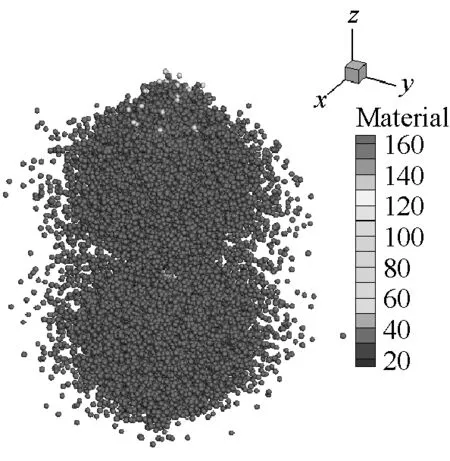
(f) t=300 μs

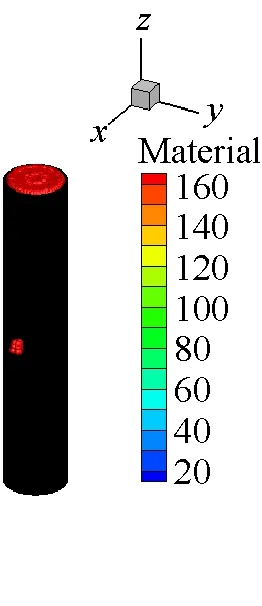
(a) t=20 μs

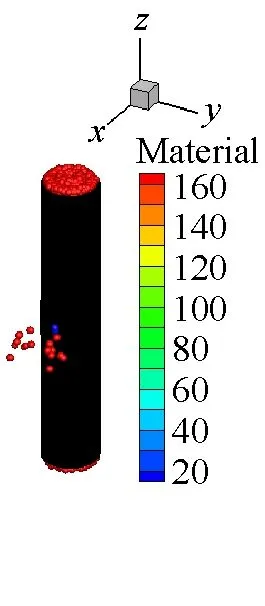
(b) t=40 μs

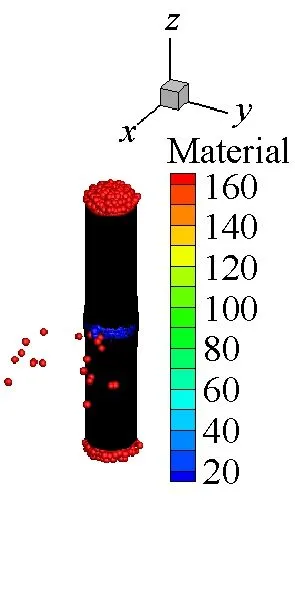
(c) t=70 μs

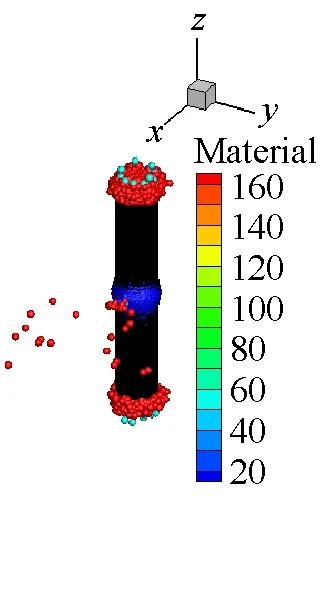
(d) t=100 μs

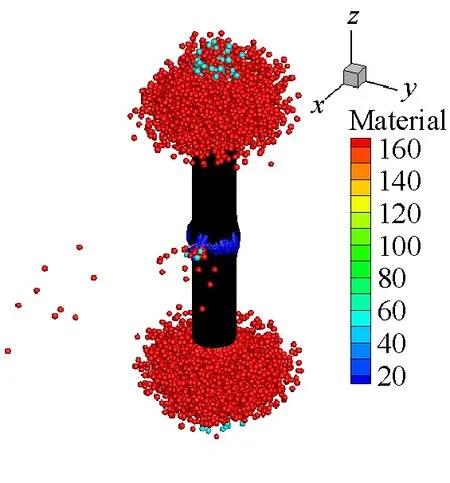
(e) t=150 μs

(f) t=200 μs

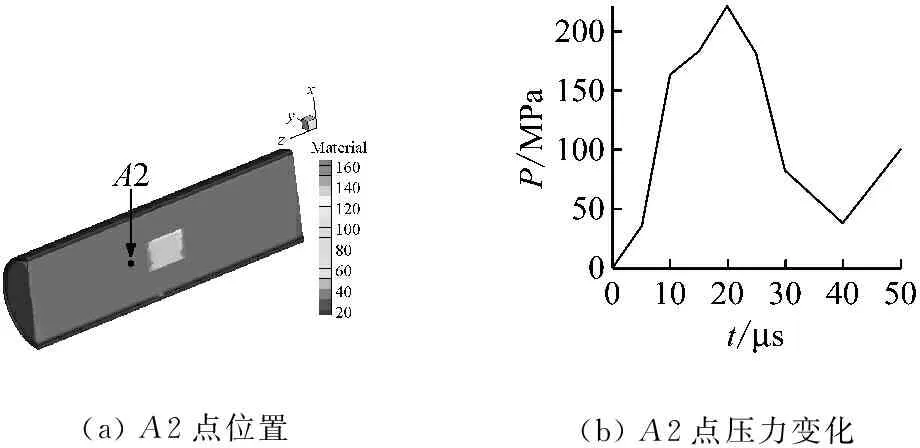
(a)A2點位置(b)A2點壓力變化

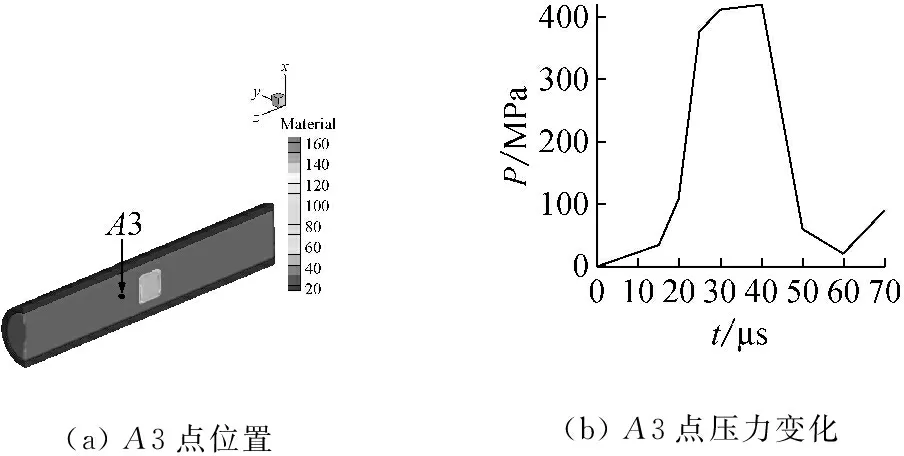
圖11 薄壁容器內測點A2處的壓力變化

圖12 厚壁容器內測點A3處的壓力變化

Fig.12 Pressure curve of pointA3 in the thick-walled vessel

5 結 論

本文建模過程中考慮空氣的影響，采用三維FEM-SPH自適應耦合算法對不同藥量下不同厚度內爆容器的爆炸響應過程進行了數值模擬。通過與實驗及LS-DYNA軟件中ALE算法的對比，表明FEM-SPH自適應耦合算法能夠有效再現帶預制孔內爆容器的爆炸鼓包過程和開孔損傷破壞過程。FEM-SPH自適應耦合算法可為容器內爆載荷作用下的動態響應提供有效的模擬計算途徑。

論文研究給出了有限單元轉化為SPH粒子的過程，表明接觸界面處的單元更先轉化為粒子。并且單元轉化為SPH粒子后，SPH方法可以較容易的捕獲內爆容器內炸藥和空氣介質的運動過程，獲得容器內測量點的壓力脈沖。論文研究結果表明，本文模型模擬結果符合內爆容器的規律特征，可為內爆容器研究提供參考。

參 考 文 獻

[1] 胡八一, 周剛, 鄭津洋,等. 爆炸容器研究及應用最新進展評述[C]// 壓力容器先進技術-第七屆全國壓力容器學術會議論文集. 無錫：中國機械工程學會，2009.

[2] LIU M B, LIU G R, ZONG Z, et al. Computer simulation of high explosive explosion using smoothed particle hydrodynamics methodology[J]. Computers & Fluids, 2003, 32(3):305-322.

[3] JOHNSON G R, STRYK R A. Conversion of 3D distorted elements into meshless particles during dynamic deformation[J]. International Journal of Impact Engineering, 2003, 28(9): 947-966.

[4] JOHNSON G R. Numerical algorithms and material models for high-velocity impact computations[J]. International Journal of Impact Engineering, 2011, 38(6): 456-472.

[5] 王吉, 王肖鈞, 卞梁. 光滑粒子法與有限元的耦合算法及其在沖擊動力學中的應用[J]. 爆炸與沖擊, 2008, 27(6):522-528.

WANG Ji, WANG Xiaojun, BIAN Liang. Linking of smoothed particle hydrodynamics method to standard finite element method and its application in impact dynamics[J]. Explosion and Shock Waves, 2008, 27 (6): 522-528.

[6] 胡德安, 孫占華, 朱婷. 三維自適應FE-SPH耦合算法在多層間隔金屬靶侵徹問題中的應用[J]. 爆炸與沖擊, 2015, 35(3):416-422.

HU Dean, SUN Zhanhua, ZHU Ting. Application of 3D FE-SPH adaptive coupling algorithm to penetration analysis of spaced multi-layered metallic targets[J]. Explosion and Shock Waves, 2015, 35(3): 416-422.

[7] MA L, HU Y, ZHENG J,et al. Failure analysis for cylindrical explosion containment vessels[J]. Engineering Failure Analysis, 2010, 17(5):1221-1229.

[8] MA L, XIN J, HU Y, et al. Ductile and brittle failure assessment of containment vessels subjected to internal blast loading[J]. International Journal of Impact Engineering, 2013, 52:28-36.

[9] 辛健, 馬利, 胡洋,等. 內爆載荷作用下不銹鋼圓柱殼的斷裂失效分析[J]. 壓力容器, 2013, 30(2):66-72.

XIN Jian, MA Li, HU Yang, et al. Fracture analysis of stainless steel tube under internal blasting loading[J]. Pressure Vessel Technology, 2013, 30(2): 66-72.

[10] LIU G R, LIU M B. Smoothed particle hydrodynamics: a meshfree particle method[M]. Hefei:World Scientific, 2003: 298-300.

[11] 楊秀敏. 爆炸沖擊現象數值模擬[M]. 北京：中國科學技術大學出版社, 2010.

[12] JOHNSON G R. Linking of lagrangian particle methods to standard finite element methods for high velocity impact simulations[J]. Nuclear Engineering and Design, 1994, 150(2/3): 265-274.

[13] JOHNSON G R, STRYK R A. Symmetric contact and sliding interface algorithms for intense impulsive loading computations[J]. Computer Methods in Applied Mechanics & Engineering, 2001, 190(35):4531-4549.

[14] JOHNSON G R, STRYK R A, BEISSEL S R, et al. An algorithm to automatically convert distorted finite elements into meshless particles during dynamic deformation[J]. International Journal of Impact Engineering, 2002, 27(10):997-1013.

[15] CAMPBELL J, VIGNJEVIC R, LIBERSKY L. A contact algorithm for smoothed particle hydrodynamics[J]. Computer Methods in Applied Mechanics & Engineering, 2000, 184(1):49-65.

[16] LINDHOLM U S, JOHNSON G R. Strain-rate effects in metals at large shear strains[J]. Springer US, 1983: 61-79.

[17] 周光坰. 流體力學. 上冊[M]. 北京：高等教育出版社, 2000.

[18] 胡八一, 柏勁松, 張明,等. 真實爆炸容器殼體動力響應的強度分析[J]. 應用力學學報, 2001, 18(3):91-95.

HU Bayi, BAI Jinsong, ZHANG Ming, et al. The dynamic response analysis of a real explosion-container vessel[J]. Chinese Journal of Applied Mechanics, 2001, 18 (3): 91-95.