微銑削中考慮時變切削力系數的顫振穩定性預測

劉 宇, 王振宇, 楊慧剛, 張義民

(1.東北大學 機械工程與自動化學院， 沈陽 110819； 2.菏澤學院 蔣震機電工程學院，山東 菏澤 274015)

隨著微銑刀加工技術的不斷提高，微銑削的應用領域也越來越廣，如芯片上的微通道總線，微型燃料電池，微噴頭，光纖微孔等。然而銑削加工過程中的再生顫振問題仍嚴重制約著機床的加工效率和工件的加工精度。

目前顫振預測的方法主要有四種：Altintas等[1]提出的定向法，該方法根據定向系數將二維銑削動力學參數定向到切削合力方向，又被稱為準單自由度法；Altintas等[2]提出的零階近似法，該方法給出了精確計算時變切削力的解析表達式，為精確近似時變的切削力提供了新的思路；Elbeyli等[3]提出的半離散法和Ding等[4]提出的全離散方法，將切削過程均分成若干等份，通過求解延時微分方程獲得銑削加工的顫振穩定性葉瓣圖。此后，研究發現由于刀具的磨損、材料的分布不均勻、測量誤差、噪聲干擾、加工環境的變化、高主軸轉速下系統的非線性問題以及是否使用冷卻液等，致使實際加工過程中切削力系數、固有頻率等都是不確定參數[5-6]，這些不確定參數又可根據是否與時間有關分為隨機參數和時變參數。穩定性葉瓣圖對模態參數的變化特別敏感，因此這些參數的變動必然對顫振穩定性預測產生很大的影響。在上述研究中，所有的方法都將加工系統的結構參數、材料切削性能參數等看作確定性量。

針對加工過程中參數的隨機性問題，有些學者提出了包含隨機參數的顫振穩定性預測方法。Duncan等首次提出了參數的不確定性對穩定性葉瓣圖的影響，指出加工過程中的頻響函數和切削力系數都是隨機參數。Park等[7]將魯棒穩定性引入到顫振預測模型中，并將固有頻率和切削力系數當作不確定參數，通過對這些參數取最大最小值并結合魯棒穩定性原理得出顫振穩定性葉瓣圖。Sims等[8]將模糊算法引入到顫振預測中，用隸屬度表示參數的變化范圍，并得到模糊穩定性葉瓣圖。Totis[9]將概率算法引入車削過程中，建立了銑削動態不確定模型，分析了系統的顫振魯棒穩定性。Liu[10]將動態結構的可靠性分析引入車削系統的顫振預測中，得到一系列不同可靠度下的顫振穩定性葉瓣圖。上述顫振預測方法雖然考慮到參數的隨機特性，但在其預測中都將隨機參數都看作時不變的，并沒有考慮因刀具磨損導致的刀刃半徑和切削力系數等參數的時變特征。

刀具磨損是一個時變的過程，因此在其影響下的刀刃半徑和切削力系數也是時變的。Li等[11]研究發現微銑削中刀具的磨損使得刀刃半徑和X，Y，Z方向上的切削力均逐漸增。Karandikar等[12]研究發現切向切削力和徑向切削力隨刀具磨損量的增加而增加。

研究表明微銑削中刀刃半徑的大小對切削力和顫振穩定性都有顯著的影響。Bierman等[13]研究表明刀刃半徑的大小對系統的顫振穩定性有顯著的影響。Afazov等[14-15]發現微銑削中刀刃半徑越大切削力越大，并用非線性方程描述了刀刃半徑與切削力系數之間的關系，繪制出了不同刀刃半徑下的穩定性葉瓣圖。Jin等[16]建立了包含刀刃半徑的切削力系數模型，考慮略刀刃半徑對過程阻尼的影響進而得到對應的顫振穩定性葉瓣圖。然而他們只是將刀具的大小當作定值忽略了刀具磨損導致的刀刃半徑的隨機性和時變問題。

針對加工參數的隨機特性和刀具磨損導致的參數的時變問題，本文將動態結構的時變可靠性分析思想引入到銑削加工系統的顫振穩定性分析中，用伽馬過程描述刀刃半徑隨切削時間的變化關系，進而得到了不同切削刻下切削力系數的大小。建立了顫振時變穩定性和顫振時變可靠性模型，分析了微銑削加工中的時變穩定性和時變可靠性并繪制出系統的時變穩定性和時變可靠度曲線。

本文的結構如下：第一部分為微銑削的力學建模，將切削力系數用含刀刃半徑的方程表示；第二部分為刀具的磨損量建模，用Gamma過程描述了刀刃半徑隨時間的變化關系；第三部分為系統顫振時變穩定性建模與分析與模型簡化，給出了包含時間信息的極限切深與顫振可靠度的數學表達式；第四部分建立了系統給的時變可靠性模型；第五部分為算例研究；第六部分為結論。

1 刀刃半徑時變規律建模

Gamma過程是一個具有獨立、非減且時間和狀態都是連續的隨機過程。其增量服從Gamma 分布。由Li等[17-18]的論文可知刀具磨損是一個典型的連續時間、 連續狀態的隨機過程，并且由于其不可自我修復，因此也是一個增量非減的過程，故本文用Gamma過程來描述刀具的磨損量與時間之間的關系。定義r(t)(其中t的單位為小時)為t時刻刀刃半徑的增量。由Gamma過程的定義可知其概率密度函數為

(1)

式中：Ga為Gamma分布函數；Γ為Gamma函數；μ，v(t)分別為伽馬分布中的尺度參數的倒數和形狀參數；I(0, ∞)為當x∈[0, ∞]時其值為1, 否則為0的函數。R(t)的均值和方差分別表示為

(2)

Moriwaki等[19]研究表明，期望的劣化值與能量規律成正比，所以刀刃半徑增量的期望值可以表示為

(3)

式中：μ、b和c都是大于零的實數，可由曲線擬合得到。所以Gamma過程中的形狀參數可以表示為

v(t)=ctb

(4)

所以在t時刻是刀刃半徑的大小可表示為

(5)

式中：r0為加工初始時刻刀刃半徑的大小；t時刻是刀刃半徑的均值可表示為

(6)

微銑刀磨損前后的形狀如圖1所示。

圖1(a)為微銑刀整體尺寸，圖1(b)為刀具磨損前的刀刃半徑大小，圖1(c)為磨損后刀刃半徑的大小。

2 包含刀刃半徑時變切削力系數建模

微銑削中由于切深較小一般在25 μm以下，微銑刀的刀刃半徑一般在3～20 μm[19]，因而刀刃半徑的變化直接影響切削力的大小。故，如何精確的建立刀刃半徑與切削力系數之間的關系成為了研究刀刃半徑對加工過程穩定性影響的關鍵。本文結合了 Jin等論文中的切削力系數模型，研究了加工時間與切削力系數之間的關系具體表達式如下

(a)(b) (c)

圖1 微銑刀磨損前后刀刃半徑的變化對比

Fig.1 Comparison of cutting edge radius between new and wear tool in micro-milling

Kt(h,r(t))=αthdt+βthptr(t)qt=

(7)

Kr(h,r(t))=αrhdr+βrhprr(t)qr=

(8)

式中：Kt，Kr分別為切向切削力系數和徑向切削力系數；α,β,d,p,q為常數。本文Deform-2D仿真技術獲取微切削材料AL6061的切削力，進而求取其切削力系數，刀具前角為5°，后角為7°，刀刃半徑r在[1,20] μm內變化，切厚h在[0.5, 20]μm內變動，進給速度為4.5 μm每刃，其余參數與Jin等均相同，網格單元尺寸為0.05μm。各參數擬合后的大小如表1所示。

表1 切削力系數的大小

3 微銑削中顫振時變穩定性建模

3.1 顫振穩定性建模

如圖2所示，我們將mx,my,kx,ky,cx,cy定義為兩自由度銑削模型在X方向和Y方向上的模態質量、模態剛度和模態阻尼，h表示曲面法向方向的動態切削厚度，h=x(t)-x(t-T)，則系統的動力學方程如下

(9)

(10)

式中：N為銑刀刀刃數；φi為第i個齒的回轉角，Ft,i,Fr,i分別為第i個齒在切向和徑向方向上的分力，其大小可以表示為

圖2 微銑削力學模型

(11)

Fr,j=KrFt,j

(12)

式中：a為軸向切深；將上述公式寫成矩陣的形式如下

(13)

式中：Kt為切向切削力系數；Δx,Δy分別為X和Y方向上當前和上一周期的位移差，即切厚。αxx,αxy,αyx,αyy為平均定向因子，其表達式分別為

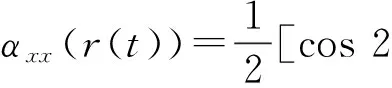
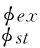
(14)

(15)

(16)

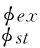
(17)

式中：φj為浸入角；φst,φex分別為銑刀的切入角和切出角，槽銑時其大小分別為0和π。Kn為徑向切削力系數與切向切削力系數的比值，具體表達式如下

Kn(h,r(t))=Kt(h,r(t))/Kr(h,r(t))

(18)

將上述時變平均定向因子代入式(20)和式(21)，然后將代入后的值代入式(19)時變特征方程，如下所示

a0(r(t))Δ2+a1(r(t))Δ+1=0

(19)

a0(r(t))=φxx(iω)φyy(iω)×

(αxx(r(t))αyy(r(t))-αxy(r(t))αyx(r(t)))

(20)

a1(r(t))=αxx(r(t))φxx(iω)+αyy(r(t))φyy(iω)

(21)

式中：φxx,φyy分別為銑削系統在X和Y方向上的頻響函數。為繪制系統的穩定性葉瓣圖我們用切削時間t處刀刃半徑的均值代替該時刻的刀刃半徑大小。求解式(19)可得系統的時變特征值λ(E[r(t)])，及其對應的時變特征值的實部Re(λ(E[r(t)]))和虛部Im(λ(E[r(t)]))。則系統在t時刻的極限切深可表示如下

(22)

(23)

(24)

3.2 顫振穩定性簡化模型

為便于計算微銑削顫振時變可靠度，我們將Kn看作常數，大小為加工初始時刻切向切削力和徑向切削力系數的比值。由式(14)～式(17)可知銑削系統的平均定向因子αxx,αxy,αyx,αyy均為常數，則同一主軸轉速在不同切削時刻下對應的特征值也是固定的，所以系統的極限切深和主軸轉速可簡化為

(25)

極限切深對應的主軸轉速可表示為

(26)

(27)

為檢驗簡化后的模型精度，本文令Kn的值為0.357 7,并在同一加工條件下選取主軸轉速分別為40 000和60 000時比較了顫振穩定性模型化簡前后其極限切深隨加工時間的變化，如圖3所示。其不同切削時刻下極限切深的波動大小如表2所示。

(a)(b)

圖3 簡化前后的極限切深對比

Fig.3 Comparison between model and simplified model of the limit cut depth

由圖3和表2可知顫振時變穩定性模型簡化后對其極限切深的影響很小，最大波動率為4.57%。所以本文在進行時變顫振穩定性預測時將徑向切削力系數和切向切削力系數的比值看作定值。

表2 模型簡化前后極限切深的波動率

4 微銑削顫振時變可靠性建模與計算

4.1 顫振時變穩定性建模

定義銑削加工過程中當軸向切深小于對應主軸轉速下的極限切深時系統可靠，否則不可靠，則系統的功能函數可以表示為

g(X)=blim-b0

(28)

式中：b0為銑削過程中加工的軸向切深；g(X)為系統失效的概率密度函數，系統的時變可靠度可以表示為

(29)

式中：XR為積分區間。定義加工過程中考慮時變參數的顫振可靠性分析為顫振時變可靠性分析。

4.2 顫振時變穩定性計算

則將式(25)代入式 (28)和式(29)可得包含時變切削力系數的功能函數和顫振時變可靠度，如式(30)、式(31)所示

(30)

(31)

由式(31)可知，在加工參數和主軸轉速一定時，刀刃半徑的大小是影響系統顫振可靠度大小的唯一因素。由式(7)和式(8)知在加工參數和主軸轉速一定時系統的切削力系數隨刀刃半徑的增加而單調遞增，因此，在加工參數和主軸轉速一定時，刀刃半徑的概率分布直接決定了系統的顫振可靠度，故系統的顫振時變可靠度可簡化成如下形式

(32)

式中：0～rtb為積分區間；XR，rtb為給定主軸轉速下的極限切深為b0時對應的刀刃半徑大小。可由式(33)求得。

(33)

由于式(33)不存在解析解，故本文采用二分法計算給定切深和主軸轉速下對應的顫振臨界點的刀刃半徑rtb大小。當rtb有解時，對式(32)進行定積分可得該時刻下的顫振可靠度

(34)

式中：γ為不完全Gamma函數具體如式(35)所示

(35)

式中：a,z,η為已知量。當式(33)無解時，若在二分法的求解范圍[ra,rb]的端點值大于零則Pr(X)=0，否則Pr(X)=1。

4.3 給定切深和主軸轉速下的極限切深和顫振可靠度曲線

顫振時變可靠度是用來描述加工過程中不發生顫振的概率。計算流程如圖4所示。

圖4 顫振時變可靠度流程圖

在銑削過程中軸向切深b0主軸轉速Ω和進給速度υ一定時，將式(6)計算得到的不同時刻下的刀刃半徑的均值代入式(9)和式(10)得時變切削力系數，然后將其先后代入式(14)～式(21)的系統在不同切削時間下的特征值。然后將其代入式(25)可得t時刻下的極限切深，由式(26)和式(27)可得對應極限切深下的主軸轉速，進而可得系統在t時刻的穩定性葉瓣圖。將計算得到的不同切削時間下的特征值代入式(33)得到積分上限rtb由式(34)可得在給定加工條件下切削時間為t時系統的顫振可靠度值。然后以時間t為橫坐標，以t時刻所對應的可靠度為縱坐標畫圖，得系統在給定切深和主軸轉速下的顫振時變可靠度曲線。

5 算例研究

5.1 擬合Gamma過程參數

Gamma過程中參數的具體數值可由數據擬合得到。實驗中采用WC/Co材料的不帶涂層的兩刃銑刀，刀刃半徑為3 μm，切削材料為AL6061。主軸轉速為65 000 r/min，進給速度為4.5 μm每齒，切深為45 μm。 實驗中刀刃半徑與切削時間的關系[20]如圖5(a)中的圓點所示。我們通過數據擬合方式獲得刀刃半徑的Gamma過程的模型參數，并繪制了刀刃半徑在不同切削時刻下的Gamma分布和均值，如圖5(a)中各時刻對應的曲線和方塊所示。其中“方塊”在“圓”和“三角形”中間，如圖5(a)中局部放大的部分。圖5(b) 為Gamma過程預測的刀刃半徑在不同切削時刻下的標準差。

(a)(b)

圖5 刀刃半徑的擬合結果

Fig.5 Fitting results of cutting edge radius

Gamma過程的擬合參數大小如表3所示。

表3 Gamma過程擬合參數

5.2 微銑削加工過程中顫振時變穩定性預測

本文選用超精密立式數控銑床(Kern Micro 2255) 進行銑削加工的顫振穩定性研究，該銑削加工系統的刀尖點模態參數[21]如表4所示。

由式(25)～式(27)可得系統在不同切削時間下的顫振穩定性葉瓣圖如圖6所示。圖6顯示隨著切削時間的增加其葉瓣圖逐漸降低。

表4 銑削系統的刀尖點模態參數

5.3 計算給定切深和主軸轉速下的系統顫振時變可靠度

圖7分別比較了顫振時變可靠度與刀刃半徑和極限切深隨切削時間的變化關系，圖7(a)顯示隨著切削時間的增加系統的刀刃半徑逐漸增加，系統的顫振可靠度逐漸降低。圖7(b)中顯示隨著切削時間的增加系統的極限切深和顫振可靠度均逐漸降低。

圖6 不同加工時刻下的穩定性葉瓣 Fig.6 Time-varyingchatterstabilitylobediagram(a)(b) 圖7 顫振可靠度與刀刃半徑和極限切深隨切削時間的對比關系 Fig.7 Therelationshipbetweenreliabilityandtooledgeradius,criticaldepthwithcuttingtime

6 結 論

微銑削加工過程由于刀具的尺寸小，主軸轉速高使得加工過程中道具磨損較快。而刀具磨損使得刀刃半徑和切削力系數隨加工時間明顯增加，進而對系統的顫振穩定性預測結果產生很大的影響，使得傳統的顫振穩定性預測方法很快失效。本文提出的顫振時變穩定性預測和時變可靠性分析方法將刀具磨損的影響考慮到顫振穩定性預測中。在不同的加工時刻上獲得了不同的葉瓣圖。并在給定切深和主軸轉速的情況下給出了系統的極限切深和顫振可靠度隨切削時間的變化關系，使得顫振預測的結果能夠準確的反應不同加工時間上的顫振穩定性。

[2] ALTINTA Y, BUDAK E. Analytical prediction of stability lobes in milling[J]. CIRP Annals-Manufacturing Technology, 1995, 44(1): 357-362.

[3] ELBEYLI O, SUN J Q, üNAL G. A semi-discretization method for delayed stochastic systems[J]. Communications in Nonlinear Science and Numerical Simulation, 2005, 10(1): 85-94.

[4] DING Y, ZHU L, ZHANG X, et al. A full-discretization method for prediction of milling stability[J]. International Journal of Machine Tools and Manufacture, 2010, 50(5): 502-509.

[5] DUNCAN G, KURDI M, SCHMITZ T L, et al. Uncertainty propagation for selected analytical milling stability limit analyses[C]//34th North American Manufacturing Research Conference.[S.l.]:[s.n.], 2006.

[6] ZHANG X, ZHU L, ZHANG D, et al. Numerical robust optimization of spindle speed for milling process with uncertainties[J]. International Journal of Machine Tools and Manufacture, 2010，61(1): 9-19.

[7] PARK S S, RAHNAMA R. Robust chatter stability in micro-milling operations[J]. CIRP Annals-Manufacturing Technology, 2010, 59(1): 391-394.

[8] SIMS N D, MANSON G, MANN B. Fuzzy stability analysis of regenerative chatter in milling[J]. Journal of Sound and Vibration, 2010, 329(8): 1025-1041.

[9] TOTIS G. RCPM—a new method for robust chatter prediction in milling[J]. International Journal of Machine Tools and Manufacture, 2009, 49(3/4): 273-284.

[10] LIU Yu. Mechanical systems and signal processing[J]. Mechanical Systems and Signal Processing, 2016，66/67(3): 232-247.

[11] LI H Z, ZENG H, CHEN X Q. An experimental study of tool wear and cutting force variation in the end milling of Inconel 718 with coated carbide inserts[J]. Journal of Materials Processing Technology, 2006, 180(1/2/3): 296-304.

[12] KARANDIKAR J M, ZAPATA R E, SCHMITZ T L. Combining tool wear and stability in high-speed machining performance prediction[D]. Gainesville: University of Florida, 2010: 7-10.

[13] BIERMANN D, BASCHIN A. Influence of cutting edge geometry and cutting edge radius on the stability of micromilling processes[J]. Production Engineering, 2009, 3(4/5): 375-380.

[14] AFAZOV S M, RATCHEV S M, SEGAL J. Modelling and simulation of micro-milling cutting forces[J]. Journal of Materials Processing Technology, 2010, 210(15): 2154-2162.

[15] AFAZOV S M, ZDEBSKI D, RATCHEV S M, et al. Effects of micro-milling conditions on the cutting forces and process stability[J]. Journal of Materials Processing Technology, 2013,213(5):671-684.

[16] JIN X, ALTINTAS Y. Chatter stability model of micro-milling with process damping[J]. Journal of Manufacturing Science & Engineering, 2013, 135(3): 1-9.

[17] 李常有, 張義民, 王躍武. 恒定加工條件及定期補償下的刀具漸變可靠性靈敏度分析方法[J]. 機械工程學報, 2012, 48(12): 162-168.

LI Changyou, ZHANG Yimin, WANG Yuewu. Gradual reliability and its sensitivity analysis approach of cutting tool in invariant machining condition and periodical compensation[J]. Journal of Mechanical Engineering, 2012, 48(12): 162-168.

[18] NOORTWIJK J M V, WEIDE J A M V D, KALLEN M J, et al. Gamma processes and peaks-over-threshold distributions for time-dependent reliability[J]. Reliability Engineering & System Safety, 2007, 92(12): 1651-1658.

[19] MORIWAKI T, TOBITO M. A new approach to automatic detection of life of coated tool based on acoustic emission measurement[J]. Journal of Engineering for Industry, 1990，112(3)：212-218.

[20] MALEKIAN M, PARK S S, JUN M B G. Modeling of dynamic micro-milling cutting forces[J]. International Journal of Machine Tools & Manufacture, 2009， 49(7): 586-598.

[21] THEPSONTHI T, ?ZELT T. 3D Finite element process simulation of micro-end milling Ti-6Al-4V titanium alloy: experimental validations on chip flow and tool wear[J]. Journal of Materials Processing Technology, 2015，221：128-145.