基于Petri網的業務過程建模

黃苾 代飛 莫啟

摘要 建模業務過程是企業實施大規模編程的核心。分析了業務過程的組成元素，討論了使用Petri網如何表示業務過程中的開始、結束、任務和路由，并通過一個例子，說明了使用Petri網建模業務過程的直觀性和易溝通、理解性。

【關鍵詞】業務過程 任務 路由 Petri網

1 引言

從20世紀70年代末到20世紀90年代初，信息系統的關注焦點是數據的存取，因此，數據庫管理系統被認為是最核心的基礎平臺。自20世紀90年代初開始，信息系統的關注焦點從數據逐步轉移到過程上來。作為這種轉變的結果，今天以業務過程驅動為代表的大規模編程（Programming-in-the-large）在工作流管理、企業應用集成、B2B電子商務、Web服務組合等領域得到了廣泛應用。因此，建模業務過程成為了企業實施大規模編程的核心。

為了解決上述問題，本文提出使用Petri網來建模業務過程。其好處在于：

（1） Petri網具有圖形化的表示，可直觀描述業務過程，便于溝通和理解;

（2） Petri網有堅實的數學基礎，建模人員可以對建模產生的業務過程模型進行分析，以確保模型的正確性。

2 業務過程

業務過程是指相關的、結構化的活動或任務的集合，它們為客戶提供特定的服務或產品。在日常的工作、學習和生活中，業務過程隨處可見。例如：辦事流程、坐飛機的安檢流程、訂單支付流程、物流流程等。

通常，業務過程都有自己的開始和結束;由許多要被執行的任務（ task）和一系列決定任務執行次序的條件構成。進一步，這些決定哪些任務需要被執行以及以何種次序執行，稱為路由。在業務過程中，路由具有四種下述四種形式：

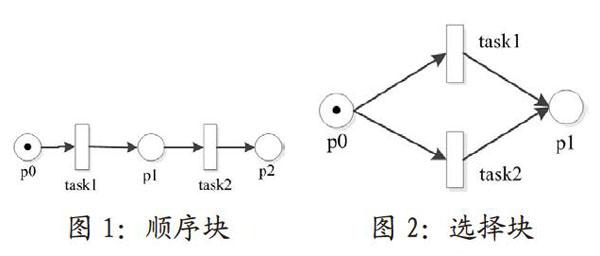
2.1 順序路由

兩個任務間順序執行。通常，這兩個任務間存在依賴關系，例如前一個任務的結果是后一個任務的輸入。

2.2 選擇路由

在兩個任務或多個多任務間選擇一個任務執行。通常，選擇需要基于相關屬性值來做決定。

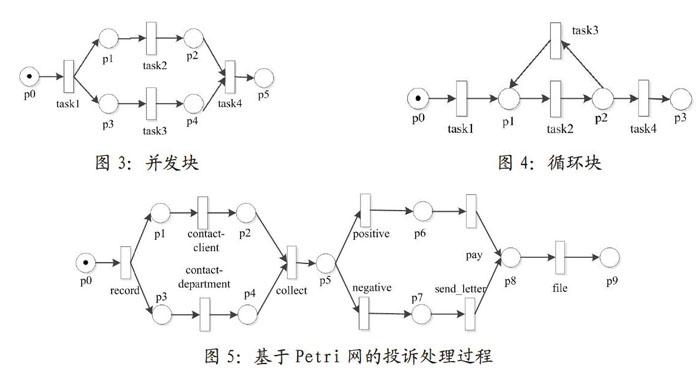
2.3 并發路由

兩個任務或多個任務能同時或以任意次序執行。通常，這些任務都需要被執行，且它們之間沒有任何依賴關系，互不影響。

2.4 循環路由

多次執行某個任務。

下面用文字描述了一個投訴處理過程。首先，步驟1：剛收到的投訴需要被記錄下來。其次，步驟2：聯系投訴的顧客和被投訴的相關部門。之后，步驟3：搜集數據并做出決策。步驟4：根據決策，或者支付賠償或者發拒信。最后，步驟5：投訴被歸檔。

3 業務過程概念到Petr i網的映射

Petri網是1962年由德國科學家CarlAdam Petri博士在他的博士論文《用自動機通信》中創立的一種網狀結構。本質上，它是一個有向二分圖，由庫所和變遷組成。

定義1（Petri網）Petri網是一個四元組S=（P，T;F，M），其中：

（1）P ∪ T≠￠，習慣稱P為庫所集，T為變遷集;

（2）P ∩ T=￠;

（3） Fc （PxT）∪（TxP），稱F為流關系;

（4）映射M：P→{O，1，2，3…）稱為Petri網的一個標識。通常用M0表示Petri網的初始標識。

通常，庫所使用圓圈表示，變遷使用方框表示，流關系使用有向線段表示，托肯使用實心小黑點表示。

當使用Petri網來建模業務過程時，用庫所表示條件，用變遷表示任務。因為，變遷是Petri網中主動元素;庫所是被動元素。

進一步，用一個沒有輸入弧的庫所來表示過程的開始，用一個沒有輸出弧的庫所來表示過程的結束。

針對路由，用圖1所示的順序塊表示順序路由;用圖2所示的選擇塊表示選擇路由;用圖3所示的并發塊表示并發路由;用圖4所示的循環塊表示循環路由。

使用Petri網建模第2節用文字描述的投訴處理過程，得到的Petri網如圖5所示。其中，庫所p0表示過程的開始;庫所p9表示過程的結束。變遷record表示步驟1;變遷contact-client和contact-department表示步驟2;變遷collect表示步驟3;變遷positive和negatlve表示步驟4;變遷file表示步驟5。

可以看出，圖5所示的投訴處理過程，比用文字描述的投訴處理過程，更加直觀，更便于溝通和理解。

4 總結

首先，討論了業務過程的組成元素：開始、結束、任務及路由;其次，提出如何用Petri網中的元素來表示業務過程的不同元素，最后，通過一個例子，充分說明了使用Petri網建模的業務過程比文字描述的業務過程更直觀，更便于溝通和理解。

參考文獻

[1]袁崇義.Petri網原理與應用[M].電子工業出版社，2005.

[2]Dumas M，Rosa M L，Mendling J，et al.Fundamentals of Business ProcessManagement [M]. Springer PublishingCompany， Incorporated，2013.

[3]Petri CA. Kommunikationmitautomaten[D]. Institut fur InstrumentelleMathematik， Schriften des IIM 2， Bonn， 1962.