探究類比推理在高中數(shù)學(xué)解題中的應(yīng)用研究

鄧志偉

【摘要】? 類比推理主要是已知兩類對象有部分相同或者類似的屬性，且在這種情況下從已知的規(guī)律去推測未知的規(guī)律。近年來類比推理已經(jīng)成為高中數(shù)學(xué)教學(xué)中比較熱門的考點(diǎn)，其不僅考察學(xué)生整體的研究能力，同時(shí)也考察學(xué)生的邏輯思維與邏輯推理能力。類比推理主要運(yùn)用于解決一些疑難問題，并且具有事半功倍的作用。而在高中數(shù)學(xué)教學(xué)中運(yùn)用類比推理法，能有效地鍛煉學(xué)生的思維，培養(yǎng)學(xué)生良好的數(shù)學(xué)素質(zhì)，有效的幫助學(xué)生學(xué)習(xí)新的知識(shí)，從而促進(jìn)學(xué)生高效率的解決數(shù)學(xué)問題。基于此，本文就類比推理在高中數(shù)學(xué)解題中的應(yīng)用進(jìn)行研究，旨在為后續(xù)的數(shù)學(xué)教學(xué)工作奠定良好的基礎(chǔ)。

【關(guān)鍵詞】? 類比推理 高中數(shù)學(xué) 解題 應(yīng)用研究

【中圖分類號(hào)】? G633.6? ?? ? ? ? ? ?【文獻(xiàn)標(biāo)識(shí)碼】? A ? ? 【文章編號(hào)】? 1992-7711（2018）12-239-01

0

前言

高中階段的數(shù)學(xué)知識(shí)整體比較復(fù)雜，為了能提供學(xué)生解題的效率，教師也不斷的思考各種快速解題的方法。其中，類比推理就是其中的一種，該方法有利于學(xué)生理解數(shù)學(xué)知識(shí)，高效的解決數(shù)學(xué)問題，被廣大教師廣泛應(yīng)用。因此，為了能夠提高學(xué)生的數(shù)學(xué)綜合能力，合理的運(yùn)用類比推理思維輔助學(xué)生解決數(shù)學(xué)問題就顯得尤為重要。接下來筆者就結(jié)合近年來高中數(shù)學(xué)教學(xué)經(jīng)驗(yàn)探討類比推理應(yīng)用在高中數(shù)學(xué)解題中的策略，希望能幫助學(xué)生提高他們的綜合能力。

二、類比推理在幾何解題中的應(yīng)用

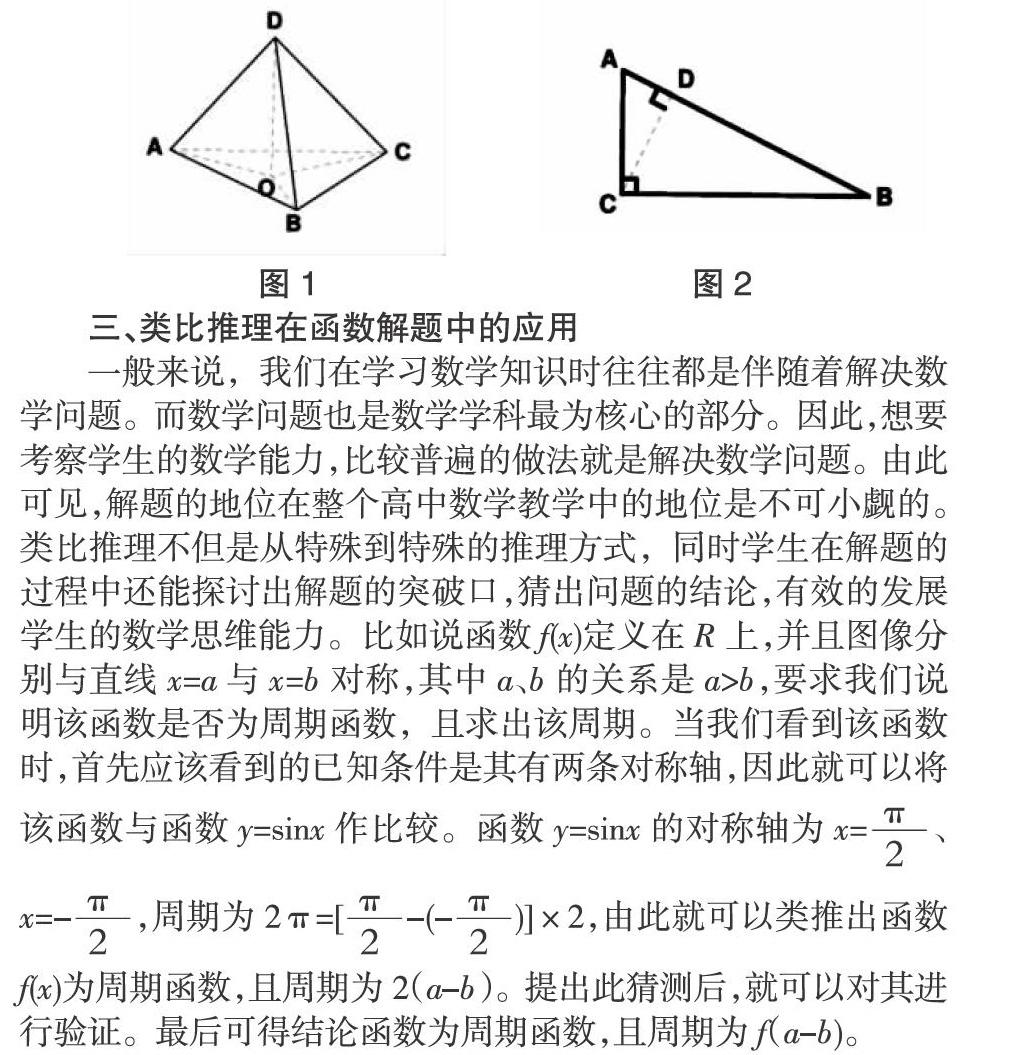
幾何也是高中階段重要的一部分內(nèi)容，平面中各種圖形的相關(guān)關(guān)系與空間立體幾何中的各種圖形相比還是比較簡單的，空間立體幾何是屬于比較抽象的內(nèi)容，大部分學(xué)生難以理解，但是組成空間圖形的還是平面中的點(diǎn)與線。比如說在解決這道證明題時(shí)：存在一個(gè)三棱柱，圖形如圖1所示，在它的三個(gè)側(cè)面中，每兩個(gè)面是互相垂直的，試著證明在這個(gè)圖形中兩個(gè)側(cè)面與底面平方的和與另一個(gè)側(cè)面的平方相等。

證明過程：在平面三角形ABC中，過點(diǎn)C想AB邊作一條垂線CD，并且點(diǎn)D是交點(diǎn)。如圖2所示。這時(shí)就可以證明出相似三角形中AC2=BD·AB，CB2=BD·AB，最后可得AC2+BC2=AB2。得此結(jié)論后，教師就可以運(yùn)用類比推理將該結(jié)論擴(kuò)展運(yùn)用于空間幾何中。過點(diǎn)D做底面ABC的垂線，把平面中的線類比為空間中的面，左后可以得出S△DAB2=S△ABC·S△ABO，S△DAC2=S△ABC·S△ACO，△DCB2=S△ABC·S△CBO，最后就可以得出S2△ACD=S2△ABC+S2△ABD+S2△BCD.通過類比推理，學(xué)生快速的解決了大部分學(xué)生公認(rèn)的難點(diǎn)問題，逐漸提高學(xué)生的數(shù)學(xué)核心素養(yǎng)。

結(jié)束語

以上就是筆者在高中數(shù)學(xué)解題教學(xué)中運(yùn)用類比推理思維解決問題的幾點(diǎn)看法，通過運(yùn)用類比推理方法解決數(shù)學(xué)問題，使得原本復(fù)雜的問題變得更加簡單，提高了學(xué)生解題的效率，可見該方法在數(shù)學(xué)學(xué)科中具有重要的意義。教師應(yīng)該有意識(shí)的培養(yǎng)學(xué)生學(xué)會(huì)正確的運(yùn)用類比推理思維，提高學(xué)生的數(shù)學(xué)水平。

[ 參? 考? 文? 獻(xiàn) ]

[1]張海葉. 探究類比推理在高中數(shù)學(xué)解題中的應(yīng)用[J]. 數(shù)學(xué)教學(xué)通訊， 2017（18）：70-71.

[2]謝有才. 類比推理法在高中數(shù)學(xué)解題中的應(yīng)用探究[J]. 數(shù)理化學(xué)習(xí)（教研版）， 2018（1）.

[3]叢茂峰. 高中數(shù)學(xué)教學(xué)實(shí)踐中類比推理的運(yùn)用[J]. 數(shù)學(xué)學(xué)習(xí)與研究：教研版， 2017（21）：90-90.

[4]陳安學(xué). 類比推理在高中數(shù)學(xué)教學(xué)實(shí)踐中的應(yīng)用研究[J]. 學(xué)周刊， 2017（21）：49-50.