柔性鉸鏈可傾瓦軸承動靜態特性研究

陳淑江， 熊文濤， 路長厚， 馬金奎

(山東大學 機械工程學院高效潔凈機械制造教育部重點實驗室， 濟南 250061)

可傾瓦軸承具有超穩定特性，廣泛應用于高速精密轉子中[1]。然而，可傾瓦軸承結構復雜，加工裝配要求高，易形成誤差累積，需要高度精確的加工裝配工藝才能滿足使用要求；其次支點磨損及大的接觸應力易引起疲勞損傷，由此放大徑向誤差；而且在使用過程中，有些頂部軸瓦可能會出現空載狀態，處于不穩定平衡，極易發生振動，甚至軸瓦撐起與軸頸接觸造成損傷。

現代加工技術的發展促進了可傾瓦軸承的創新設計，出現了柔性鉸鏈可傾瓦軸承。采用電火花線切割加工技術，將軸瓦與軸承殼體通過彈性薄梁結構(柔性鉸鏈)連接為一體，使其替代擺動支點。美國一些學者對此類軸承進行了實驗及應用研究，給出了該軸承的加工方法，并獲得這種軸承形式無軸瓦顫振和誤差累積，無接觸應力，允許軸線偏斜，且該軸承具有更低的能耗及良好的動態穩定特性，同時在實際工程應用中保證了使用可靠性[2-3]。De Choudhury等[4]對四瓦柔性鉸鏈可傾瓦軸承進行了包括油液溫升、流量、摩擦功耗及瓦溫等靜特性測量，較同規格的可傾瓦軸承具有更低的能耗。Zeidan也提供了二者的比較，并且注意到當轉子低于第二臨界速度時，普通可傾瓦軸承由于支點磨損會導致第二臨界速度下降，使得共振點更接近轉速，而柔性鉸鏈可傾瓦軸承則無此問題。

Armentrout等[5]、Zeidan等[6]討論了柔性鉸鏈可傾瓦軸承設計參數和運行條件，并對軸承剛度和阻尼特性進行了研究。Armentrout等還討論了鉸鏈旋轉剛度對軸承橫向剛度、阻尼和穩定性的影響，并計算了鉸鏈循環應力低于材料疲勞極限，保證軸承使用可靠性。Chen[7]給出了該可傾瓦軸承考慮鉸鏈剛度的動態系數一般計算方法。

對柔性鉸鏈可傾瓦軸承的一些性能實驗測試。Walton等[8]測量了瓦間受靜載條件下的軸承特性，得到軸承直接剛度隨載荷增大而增大，而交叉耦合剛度則可忽略。San Andres等[9]繼續補充了此前工作，將承載方式變為瓦上受載，同樣獲得良好特性。

綜上可知，國外學者對該軸承的優越性能進行了相關研究，卻未對柔性鉸鏈結構及設計有詳細闡述與研究。因此，本文結合柔性鉸鏈的特性，針對一種橢圓型柔性鉸鏈可傾瓦軸承，在柔性鉸鏈剛度建模的基礎上，通過建立軸瓦油膜厚度模型及軸頸和軸瓦受力平衡模型，采用有限差分法及牛頓迭代法，研究柔性鉸鏈旋轉剛度對軸承的動靜態性能的影響規律，并提出滿足高穩定性要求的柔性鉸鏈旋轉剛度數據范圍，為柔性鉸鏈可傾瓦軸承的設計應用提供參考。

1 柔性鉸鏈計算建模

柔性鉸鏈結構多樣，主要分為直梁型、直圓型、橢圓型三種。將柔性鉸鏈與軸承應用相結合，就是利用柔性鉸鏈的旋轉剛度小而徑向剛度大的特點，從而保證軸瓦的旋轉特性及軸承的承載能力。直梁型柔性鉸鏈偏轉位移大，但偏轉精度低，直圓型柔性鉸鏈則偏轉位移小，而橢圓型柔性鉸鏈具有較小的旋轉剛度同時可保證旋轉精度[10]，因此根據軸承軸瓦旋轉特性，柔性鉸鏈選擇橢圓型結構。

當軸瓦受到油膜力作用時，產生的等效油膜力和力矩會對柔性鉸鏈產生附加的力和彎矩作用。就柔性鉸鏈本身而言，其所受的復雜外力總是可以轉化為通過柔性鉸鏈一端的三維坐標軸上的力和彎矩的合成，而另一端為固定端。如圖1所示，ξ-η為鉸鏈計算坐標系，軸瓦等效作用力及力矩(Fξ,Fη,Mδ)，t為鉸鏈最小厚度，a,b為橢圓長短半軸，φmax為橢圓圓心角，h(φ)為圓心角φ處的鉸鏈厚度，dφ,dx為計算微元。

圖1 橢圓柔性鉸鏈結構Fig.1 Calculation model of elliptical flexure hinge

柔性鉸鏈柔度矩陣

(1)

則剛度矩陣為柔度矩陣的逆

(2)

其中軸瓦徑向剛度和鉸鏈旋轉剛度分別為：

(3)

(4)

式中:具體柔度計算可參照文獻[10]。

2 柔性鉸鏈可傾瓦軸承計算建模

2.1 計算建模

如圖2所示，坐標系XOY固結在軸承中心，O、OJ、Ok分別是軸承中心、轉軸中心和第k塊瓦塊的圓心。φ為軸瓦坐標系下每個瓦塊的弧坐標，φp為每個瓦塊的支點位置角，e為偏心距，θ為偏位角，δ為瓦塊產生擾動時鉸鏈變形角，ξ-η為鉸鏈計算坐標系，rs為轉軸半徑，rb為軸承半徑，rp瓦塊內表面半徑，Ω為軸轉動角速度。

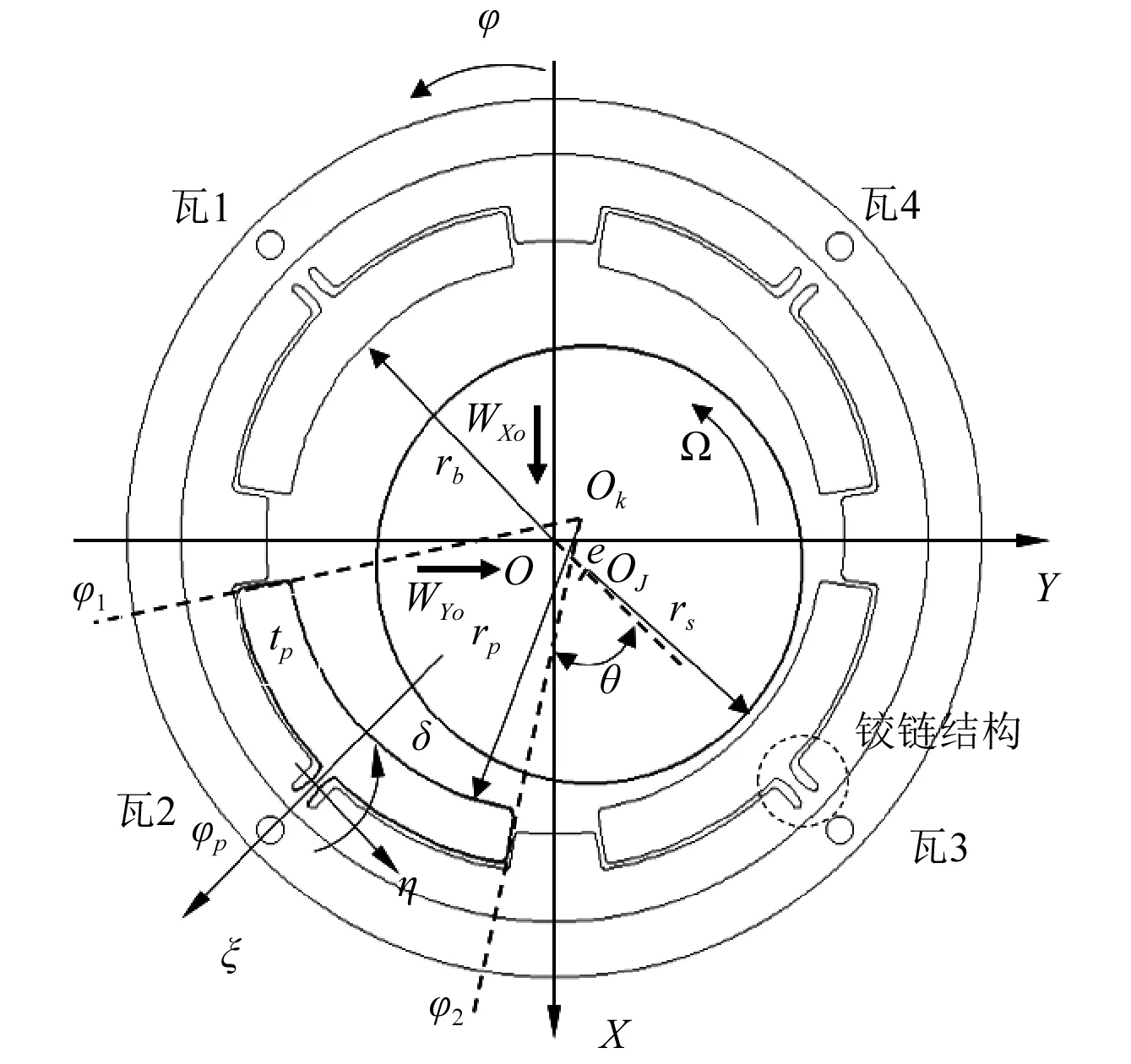
圖2 柔性鉸鏈可傾瓦軸承幾何模型Fig.2 Calculation model of flexure-pivot tilting pad journal bearings

2.2 油膜厚度

由圖2幾何關系得到柔性鉸鏈可傾瓦軸承第塊軸瓦的油膜厚度表達式

hk=cp+eXcosφ+eYsinφ+(ξp-mcp)×cos(φ-φp)+(ηp-δpr)sin(φ-φp)

(5)

式中:cp為軸瓦間隙;eX、eY分別為軸頸中心的位移;m為預載荷系數。δp為瓦塊產生擾動時鉸鏈旋轉角，ξp為瓦塊的徑向位移，ηp為橫向位移。

令無量綱油膜厚度

(6)

2.3 雷諾方程

旋轉軸頸與軸瓦內面之間形成油膜，產生油膜壓力， 則無量綱雷諾方程為：

(7)

2.4 平衡擾動分析

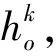
(8)

(9)

則厚度隨時間變化

(10)

其中油膜厚度增量

Δhk=ΔeXcosφ+ΔeYsinφ+Δξpcos(φ-φp)+(Δηp-Δδpr)sin(φ-φp)

(11)

油膜壓力隨時間變化

(12)

其中油膜力增量

(13)

在靜態平衡位置壓力(po)分布[11]有：

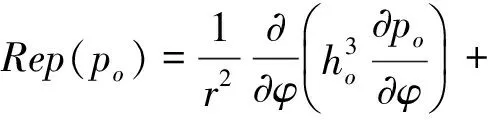
(14)

由軸頸中心位置運動產生的擾動壓力(Pα)分布[11]為：

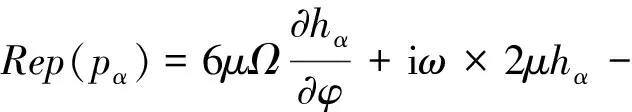
(15)

α=X,Y,hX=cosφ,hY=sinφ

對式(14)、式(15)無量綱化

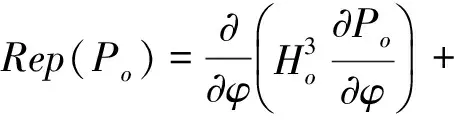
(16)

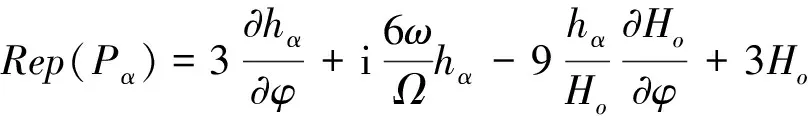
(17)

由于擾動壓力與平衡壓力計算格式類似，故都采用有限差分法[12]和逐點松弛迭代法求解，平衡壓力求取邊界條件為雷諾邊界條件，擾動壓力求取邊界條件為邊界擾動壓力為零。

3 平衡迭代計算

3.1 迭代流程圖

采用牛頓迭代法尋找負載條件下軸頸及各軸瓦的平衡位置，采用MATLAB編程[13]，并計算軸承性能，流程圖如圖3所示。

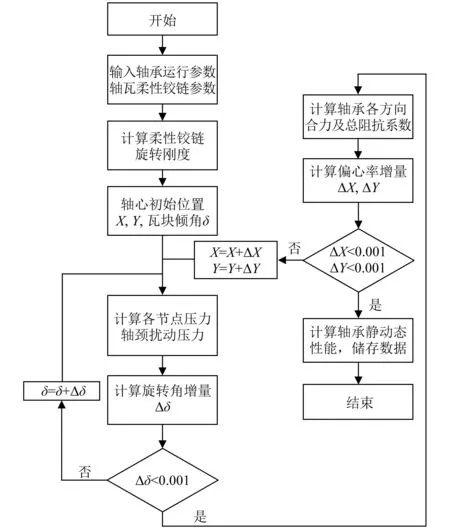
圖3 迭代計算流程圖Fig.3 Process of iterative calculation

3.2 軸瓦及軸頸受力分析

根據質量慣性矩及平行軸定理，瓦塊對鉸鏈支點的慣性矩為：

(18)

式中:ρ為材料密度;α為瓦塊包角;R0為中心到支點的距離;r0是瓦塊外表面半徑，并假設鉸鏈支點處于軸瓦外表面。

對第k塊軸瓦油膜壓力積分并無量綱化即得

(19)

由于軸瓦徑向及橫向剛度較旋轉剛度大，故只考慮旋轉彎矩Mδ對瓦作用，其中旋轉彎矩

(20)

式中：r0=rp+tp,tp為軸瓦厚度。

普通可傾瓦軸承軸瓦在平衡時，油膜作用合力矩為0，而柔性鉸鏈旋轉變形時存在反力矩Mpδ為：

(21)

油膜力及力矩由靜態和動態兩部分組成，設Z=K+iωC，則軸瓦受力表達式為：

(22)

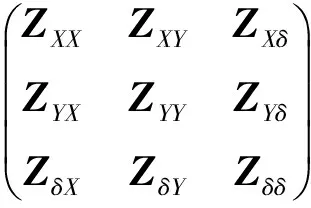
軸瓦旋轉產生的動態壓力區域滿足以下關系：

pδ=r0(pXsinφp-pYcosφp)

(23)

則阻抗矩陣各系數為：

(24)

α=X,Y,δ

其中油膜力阻抗系數及軸承等效阻抗系數為：

(25)

α,β=X,Y

(26)

3.3 軸頸平衡迭代

軸頸平衡位置第N次與第N+1次迭代，軸頸水平及豎直位置及各軸頸位移增量為：

(27)

(28)

式中:WX、WY分別為兩個方向上的不平衡載荷。

3.4 軸瓦旋轉平衡迭代

軸瓦平衡位置第N次到第N+1次迭代，軸瓦位置轉角和軸瓦旋轉位移增量分別為：

(29)

(30)

4 算例與分析

根據動靜態特性及穩定性計算公式，討論了不同柔性鉸鏈旋轉剛度下軸承特性變化，并根據鉸鏈旋轉剛度大小將整個區域分為可傾瓦區域、轉換區域、固定瓦區域。計算軸承參數如表1所示。

柔性鉸鏈可傾瓦軸承的特性位于固定瓦軸承與傳統可傾瓦軸承之間，取決于軸瓦鉸鏈支承的旋轉剛度。當鉸鏈旋轉剛度較大時，柔性鉸鏈軸承表現為固定瓦軸承；當鉸鏈旋轉剛度較小時，則表現為可傾瓦軸承。如圖4所示，軸心平衡位置隨著鉸鏈旋轉剛度的增加，軸心平衡位置偏離豎直方向，即偏位角越大。當鉸鏈旋轉剛度小時，軸心平衡位置靠近豎直方向，表現為可傾瓦軸承特性，偏心距小；當旋轉剛度大時，表現為固定瓦軸承特性，偏心距大。

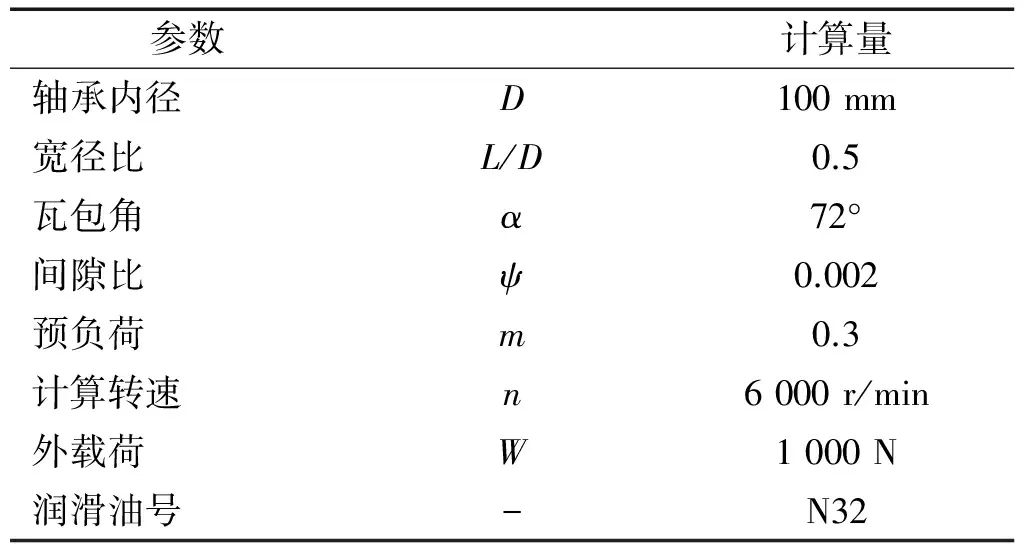
表1 軸承計算參數表

圖4 軸心平衡位置與鉸鏈旋轉剛度關系Fig.4 Shaft center eccentricity vs rotational stiffness

如圖5、6所示，隨著鉸鏈旋轉剛度增加，軸承摩擦因數及功耗在進入轉換區域出現減小，表明柔性鉸鏈可傾瓦軸承較可傾瓦軸承有更小的功耗。當進入轉換區域軸承流量增大，溫升則減小，最終到達固定瓦區域則繼續保持基本不變。由此可見，柔性鉸鏈可傾瓦軸承比固定瓦軸承具有更小流量，油的溫升則高一些。這是因為在同等承載力下，柔性鉸鏈可傾瓦軸承由于軸瓦能夠在油膜力作用下發生偏轉，形成更薄的楔形油膜，產生較大的承載力，因此流量更小，溫升更大。圖7所示為各瓦擺角及最小油膜厚度(位于軸瓦終止邊)隨鉸鏈旋轉剛度變化的規律，各瓦擺角在可傾瓦區域保持不變，到達轉換區域則變小，到達固定瓦區域則變為0。最小油膜厚度對上部瓦1和瓦4油膜厚度則逐漸增大，可見由于軸瓦的旋轉使最小油膜厚度減小20%，而作為主要承載瓦，下部瓦2和瓦3油膜厚度則先增大后減小。

圖5 流量/溫升與鉸鏈旋轉剛度關系Fig.5 Bearing flow & temperature rise vs rotational stiffness

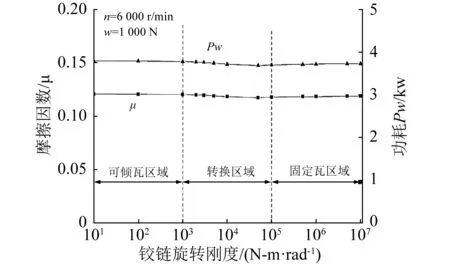
圖6 摩擦因數/功耗與鉸鏈旋轉剛度關系Fig.6 Friction factor & power loss vs rotational stiffness

圖8和圖9表明了四瓦柔性鉸鏈可傾瓦軸承在n=6 000 r/min，W=1 000工況下，采用圖2所示的瓦塊布置形式時，軸承的主剛度、交叉耦合剛度以及阻尼隨鉸鏈旋轉剛度的變化規律，當鉸鏈旋轉剛度減小時，交叉耦合剛度很小，幾乎為零，軸承表現為可傾瓦軸承特性，當鉸鏈旋轉剛度增大時，交叉耦合剛度以相反的符號對稱增加，而主剛度變化則始終保持一致，但在固定瓦區域迅速減小，表現為固定瓦軸承特性。阻尼則與鉸鏈旋轉剛度關系不大，始終保持不變，只是在轉換區域有微小的變動。

ZEIDAN在文獻[14]中給出了交叉耦合剛度對轉子動力不穩定性影響的解釋，他指出作用于轉子的不穩定性正比于交叉耦合剛度差。因此，固定瓦軸承由于交叉耦合剛度差較大，相應的固定瓦軸承支承的轉子穩定較差，而可傾瓦軸承支承的轉子則相反，穩定性較高。

圖7 各瓦擺角/最小油膜厚度與鉸鏈旋轉剛度關系Fig.7 Min film & pad rotational angle vs rotational stiffness

圖8 軸承剛度與鉸鏈旋轉剛度關系Fig.8 Stiffness coefficients vs rotational stiffness

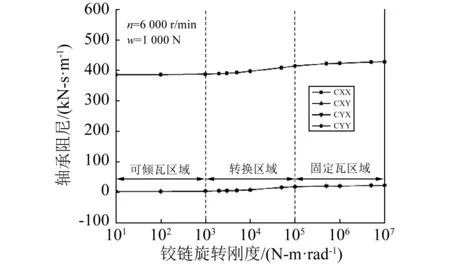
圖9 軸承阻尼與鉸鏈旋轉剛度關系Fig.9 Damping coefficients vs rotational stiffness

圖10為柔性鉸鏈旋轉剛度對軸承的渦動頻率比及軸承交叉剛度的影響曲線。交叉耦合剛度差隨鉸鏈旋轉剛度的變化規律與渦動頻率比是一致的。而通常渦動頻率比被用來表示軸承的穩定性。對固定瓦軸承而言，渦動頻率比為0.5，數值上最大可實現的穩定轉速為轉子固有頻率的2倍；而可傾瓦軸承渦動頻率比則為0，從交叉耦合剛度差引起的不穩定能也能得出可傾瓦軸承的穩定性較高。而柔性鉸鏈可傾瓦軸承由于結構的原因，鉸鏈旋轉剛度一般低于5 000 N·m/rad，由此渦動頻率比低于0.1，由此可實現的穩定速度較固定瓦軸承提高了5倍；而當鉸鏈旋轉剛度低于1 000 N·m/rad時，可達到可傾瓦軸承的較高穩定性。

圖10 渦動頻率比/交叉耦合剛度差與鉸鏈旋轉剛度關系Fig.10 Whirl frequency ratio & difference cross-coupled stiffness coefficients vs rotational stiffness

由以上分析可知，在鉸鏈設計時保證鉸鏈旋轉剛度在1 000 N·m/rad以內時，可達到類似于普通可傾瓦軸承的穩定性要求。因此可以根據柔性鉸鏈剛度計算公式設計旋轉剛度對應于1 000 N·m/rad以內的柔性鉸鏈結構及參數。

5 結 論

(1)柔性鉸鏈可傾瓦軸承作為一種新型軸承，在保證一定的穩定性的同時，具有很好的支承剛度，較同等規格的可傾瓦軸承有更低的功耗和溫升。

(2)柔性鉸鏈旋轉剛度越小，軸承的交叉耦合剛度之差與其渦動頻率比越小，軸承性能越接近傳統可傾瓦軸承特性，因此通過合理設計，采用柔性鉸鏈結構替代傳統可傾瓦軸承的擺動支點不僅可大幅度簡化軸承結構，還可以可滿足可傾瓦軸承的穩定特性。

(3)在本文的研究條件下，當柔性鉸鏈旋轉剛度在低于1 000 N·m/rad時，可以獲得較好的軸承綜合性能。因此在設計柔性鉸鏈可傾瓦軸承時，可參照最高柔性鉸鏈旋轉剛度設計對應的鉸鏈結構參數。

[ 1 ] 張直明. 計入支點彈性和阻尼時可傾瓦軸承支撐的轉子系統的動力穩定性[J]. 機械工程學報, 1983,19(2)：9-21．

ZHANG Zhiming. Rotor system’s dynamic stability with the titling-pad journal bearing reckoning in pivot stiffness and damping[J]. Chinese Journal of Mechanical Engineering, 1983, 19(2): 9-21

[ 2 ] ZEIDAN F. Developments in fluid film bearing technology [J]. Turbomachinery International, 1992, 33(6): 24-31.

[ 3 ] ANDRéS L S. Turbulent flow, flexure-pivot hybrid bearings for cryogenic applications [J]. Journal of Tribology, 1996, 118(1): 190-200.

[ 4 ] DE CHOUDHURY P, HILL M R, PAQUETTE D J. A flexible pad bearing system for a high speed centrifugal compressor [C]. 1992: 187-209.

[ 5 ] ZEIDAN F, PAQUETTE D J. Application of high speed and high performance fluid film bearings in rotating machinery [C]. Proceedings of the Twenty Third Turbomachinery Symposium，1994: 147-169.

[ 6 ] ARMENTROUT R W, PAQUETTE D J. Rotor dynamic characteristics of flexure-pivot tilting-pad journal bearings [J]. Tribology Transactions, 1993, 36(3): 443-451.

[ 7 ] CHEN W J. Bearing dynamic coefficients of flexible-pad journal bearings [J]. Tribology Transactions, 1995, 38(2): 253-260.

[ 8 ] WALTON N V, ANDRéS L S. Measurements of static loading versus eccentricity in a flexure-pivot tilting pad journal bearing [J]. Journal of Tribology, 1997, 119(2): 297-304.

[ 9 ] ANDRéS L S, JACKSON M C. Measurements of the static load (on pad) performance and pad temperatures in a flexure-pivot tilting-pad bearing [J]. Tribology Transactions, 1998, 41(2): 225-232.

[10] 陳貴敏, 劉小院, 賈建援. 橢圓柔性鉸鏈的柔度計算[J]. 機械工程學報, 2006, 42(增刊1): 111-115.

CHEN Guimin, LIU Xiaoyuan, JIA Jianyuan. Compliance calculation of elliptical flexure hinge [J]. Chinese Journal of Mechanical Engineering, 2006, 42(Sup1): 111-115.

[11] 李元生, 敖良波, 李磊, 等. 滑動軸承動力特性系數動態分析方法[J]. 機械工程學報, 2010, 46(21): 48-53.

LI Yuansheng, AO Liangbo, LI Lei, et al. Dynamic analysis method of dynamic character coefficient of hydro-dynamic journal bearing[J]. Chinese Journal of Mechanical Engineering, 2010, 46(21): 48-53.

[12] 謝帆, 荊建平, 萬召, 等. 基于有限差分法的徑向滑動軸承油膜壓力分布計算[J]. 潤滑與密封, 2012, 37(2): 12-15.

XIE Fan, JIN Jianping, WAN Zhao, et al. Calculation of oil film pressure distribution of journal bearing based on finite difference method [J]. Lubrication Engineering, 2012, 37(2): 12-15.

[13] 敏政, 王樂, 魏志國, 等. 基于MATLAB技術的滑動軸承油膜壓力分布的模擬[J]. 潤滑與密封, 2008, 33(8): 51-53．

MIN Zheng, WAN Le, WEI Zhiguo, et al. Simulation on pressure distribution of sliding bearing based on MATLAB technology [J]. Lubrication Engineering, 2008, 33(8): 51-53.

[14] ZEIDAN F. Fluid film bearing fundamentals and failure analysis [C]. Proceedings of the 20th Annual Turbomachinery symposium, 1991: 161-186.