基于頻響函數虛部的梁結構損傷檢測

張宇飛 ， 王山山

(1.河海大學 力學與材料學院，南京 210098；2.中國電建集團華東勘測設計研究院有限公司，杭州 311122)

梁結構是一種結構中承受荷載的主要常用構件，但梁結構在使用過程中由于各種原因會產生不同程度的損傷。這些結構中存在的損傷往往會影響結構的正常使用, 嚴重的損傷還會產生災難性的后果。 所以梁結構的損傷檢測問題一直在航空、機械以及土木工程等領域受到研究者的關注和重視。

現有的基于頻率、剛度和柔度等檢測方法，要么存在檢測精度不高的問題，要么需要結構未損傷前的模態信息，這些問題均限制了以上方法在工程界的應用[1-4]。因此，目前國內外基于動力測試的結構損傷檢測的研究方向主要集中于如何利用結構損傷后的動力學特性或者動力學響應來進行損傷識別。Pandey等[5]提出了一種以曲率模態作為識別和定位結構損傷的方法。狄生奎等[6]提出了基于柔度曲率差變化率的系桿拱橋損傷檢測的方法。曹暉等[7]根據模態曲率，提出了一種新的判定損傷的指標。王山山等[8]提出了檢測損傷的局部因子法，并證明了該方法在檢測和定位損傷方面的有效性與簡便性。張宇飛等[9]提出了基于隨機振動相干函數的梁結構損傷檢測法，并通過懸臂梁動力試驗，驗證了該方法能有效識別梁結構單損傷和多損傷。Liu等[10]通過研究發現，歸一化的頻響函數虛部差與模態差在結構自振頻率下存在著對應關系。并指出，頻響函數虛部能夠有效的對結構損傷進行識別。高海洋等[11]基于頻響函數虛部，將模態曲率的方法應用到板結構的損傷檢測中，并指出虛部指標具有一定的抗干擾性。

基于上述原因，本文以鋼質懸臂梁為研究對象，提出了基于頻響函數虛部的梁結構損傷檢測方法。依據模態曲率提出了判別損傷的指標CIFF(imaginary part of frequency response function curvature)，該指標考慮了系統誤差與噪聲干擾。試驗結果表明該方法能有效地對梁結構損傷進行識別。

1 CIFF理論推導

n自由度系統的頻響函數方程可表示為：

(1)

所以，頻響函數的虛部為：

(2)

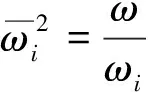
則在頻率ωi下，頻響函數虛部振型可表示為：

(3)

由中心差分公式可得，l點處頻響函數虛部振型曲率可表示為：

(4)

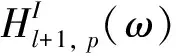
若梁結構無損傷，則頻響函數虛部振型曲率是連續變化的，可以表示成形函數：

(5)

將形函數曲線上每個點對應的值與該點實際的曲率值做差，則得到損傷指標數：

δl, p(ω)=|Cl, p(ω)-SFl, p(ω)|

(6)

在頻率ω下，取δl, p(ω)中最小的(δl, p(ω))min作為系統誤差與噪聲干擾。進行最小歸一化，構造第i階模態下測點的損傷判別因子：

(7)

考慮前m階模態對損傷判別因子的貢獻，則損傷判別因子CIFF為：

(8)

綜合上述，可根據CIFF的大小和出現的位置判別損傷程度與損傷位置。

2 試驗過程

本試驗研究對象為鋼質懸臂梁結構，材料為鋼Q345，尺寸為450 mm×16 mm×16 mm。本次試驗激振設備采用DY-300-2-0電動振動臺(如圖1所示)，施加水平向荷載。試驗數據測量以及信號采集和分析設備均采用PSV-400型激光掃描測振儀(如圖2所示)。該儀器利用激光多普勒測振技術，可以非接觸式的測量結構表面振動加速度，相比與傳統加速度傳感器該儀器對于實驗試件無任何附加質量，測量快速準確。

圖1 懸臂梁與振動臺Fig.1 Cantilever beam and shaking table

圖2 激光掃描儀Fig.2 Polytec scanning vibrometer

將懸臂梁從懸臂端到固結端設置41個測點與41個單元，每個測點處在相應單元的中間位置，如圖3所示。每個測點之間的間距為1.08 cm，距懸臂端和固結端各有0.36 cm的掃描盲區。

圖3 懸臂梁測點、單元示意圖Fig.3 The points and elements of cantilever beam

設置兩種工況的損傷：①11號單元的背面設置深4 mm的裂縫損傷；②11號單元的背面設置深6 mm的裂縫損傷，21號測點的背面設置設置深4 mm的裂縫損傷。

首先對懸臂梁進行掃頻試驗，確定其自振頻率。圖4～圖5為測點15在無損傷情況下掃頻試驗中的典型速度時程曲線圖，和經FFT變換后的頻譜曲線圖。

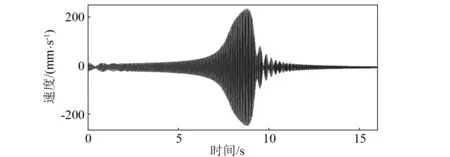
圖4 測點15第一階典型時程曲線圖Fig.4 The typical first-order speed-time curve of point 15

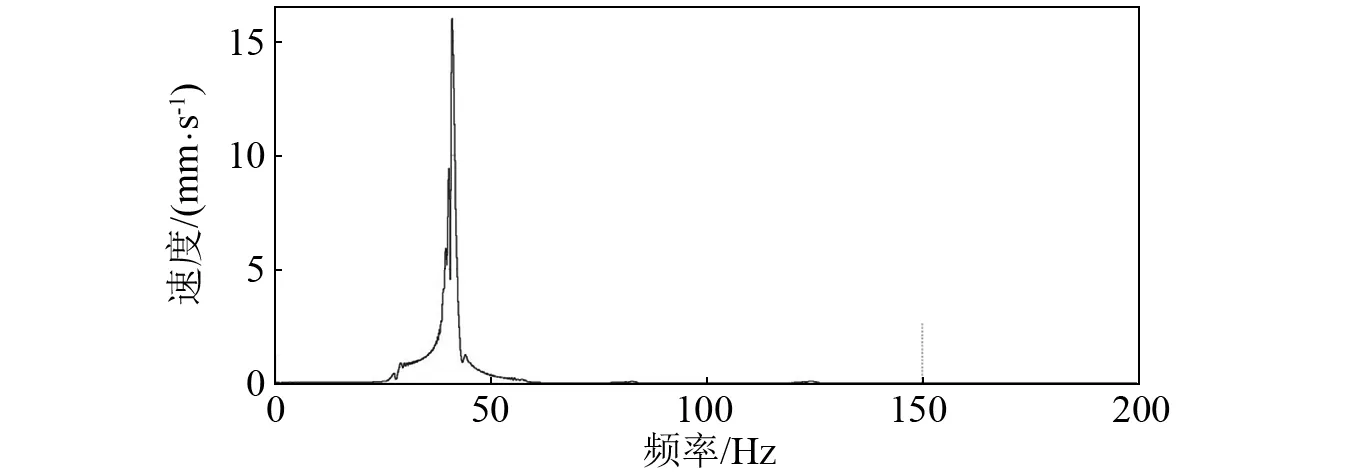
圖5 測點15第一階典型頻譜曲線Fig.5 The typical first-order FFT curve of point 15

由圖4、圖5可知，無損傷情況下懸臂梁第一階自振頻率分別為41.25 Hz。

同理，可得各工況下，懸臂梁前四階自振頻率，如表1所示。

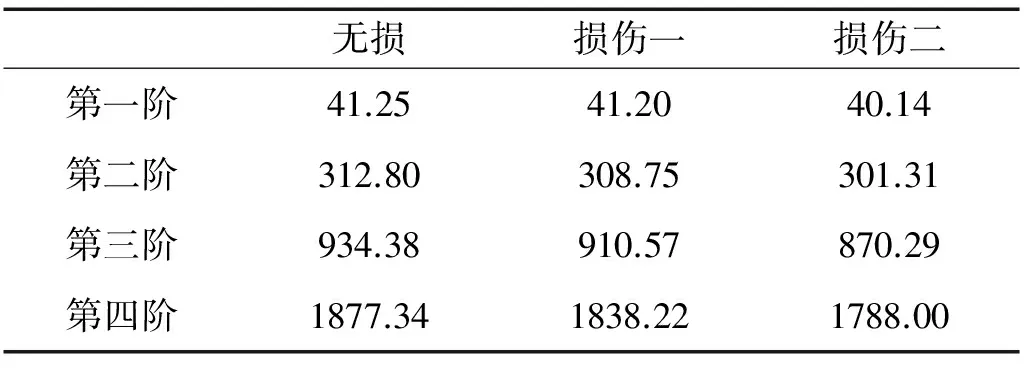
表1 各工況下懸臂梁前四階自振頻率

由于本試驗中振動臺所施能加的荷載頻率范圍在5～2 000 Hz之間，所用本試驗選取懸臂梁的前四階自振頻率為研究對象。

分別在兩種損傷工況下進行隨機試驗，所施加的平穩隨機荷載的頻率范圍分別為：20～60 Hz、280～330 Hz、840～940 Hz和1 750～1 880 Hz，加速度功率譜密度大小為3 (m·s-2/Hz)，激勵的方向為水平方向。

圖6～圖7分別為兩種損傷工況下，測點15的典型隨機響應速度時程曲線。

圖6 損傷一下測點15典型隨機響應速度時程曲線Fig.6 The typical speed random response curve of point 15 on first damage case

圖7 損傷二下測點15典型隨機響應速度時程曲線Fig.7 The typical speed random response curve of point 15 on second damage case

3 試驗結果與分析

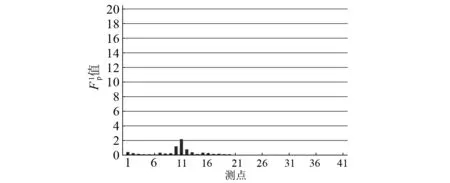
圖8 損傷一情況下各測點第一階 值Fig.8 The first order amplitude of on first damage case

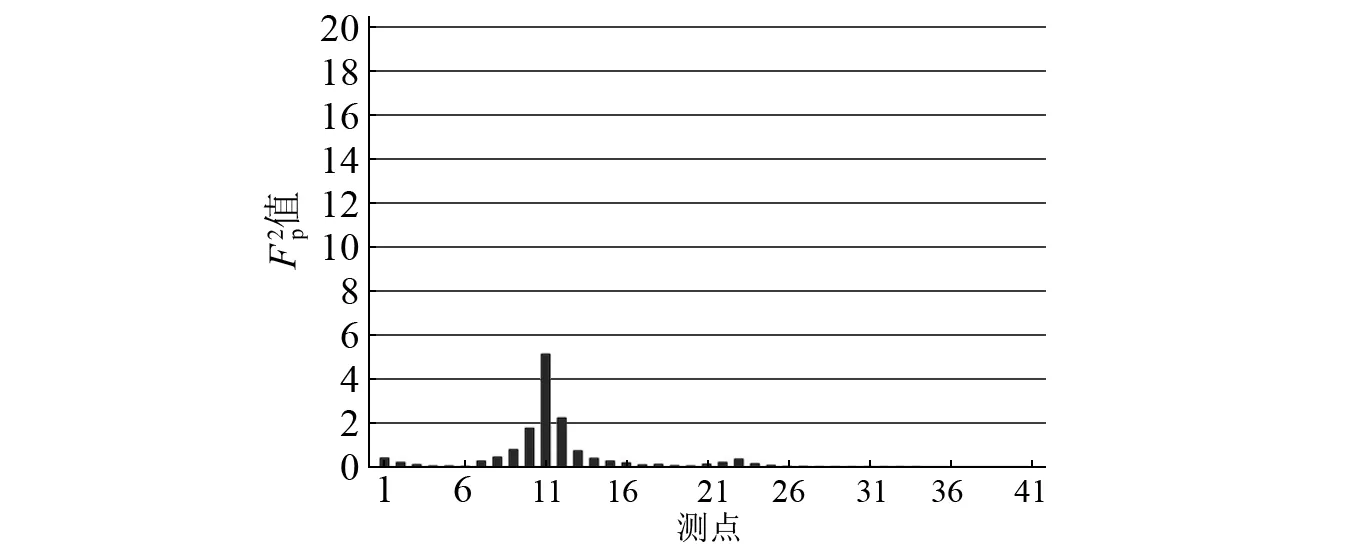
圖9 損傷一情況下各測點第二階 值Fig.9 The second order amplitude of on first damage case

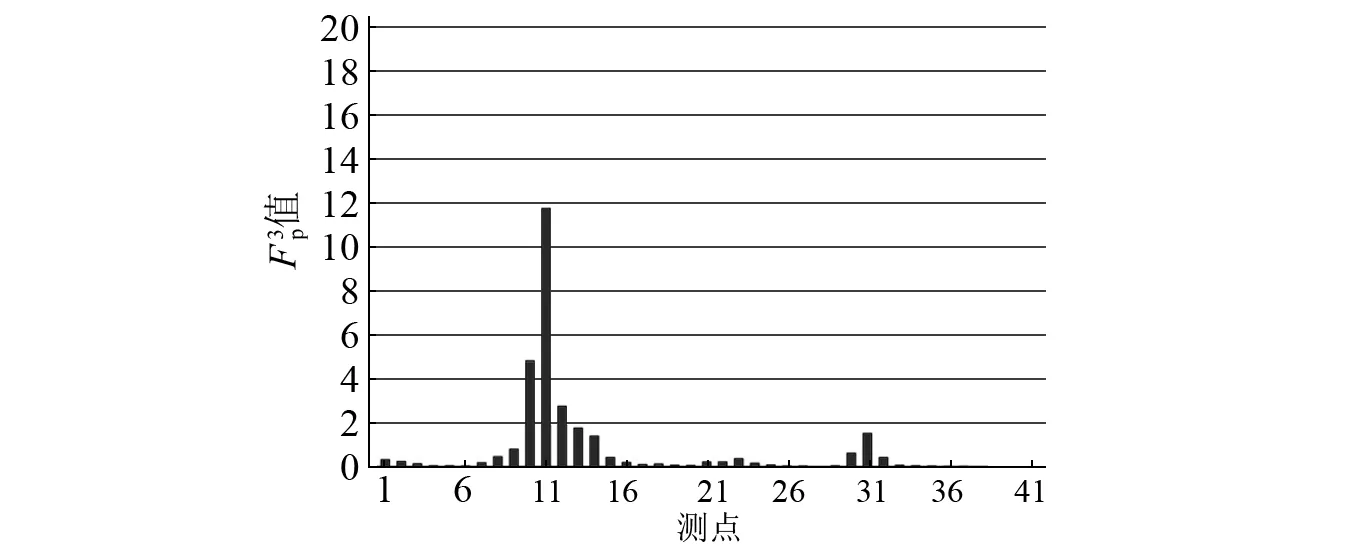
圖10 損傷一情況下各測點第三階 值Fig.10 The third order amplitude of on first damage case

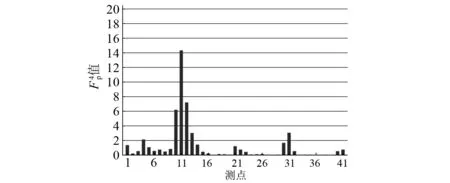
圖11 損傷一情況下各測點第四階 值Fig.11 The fourth order amplitude of on first damage case

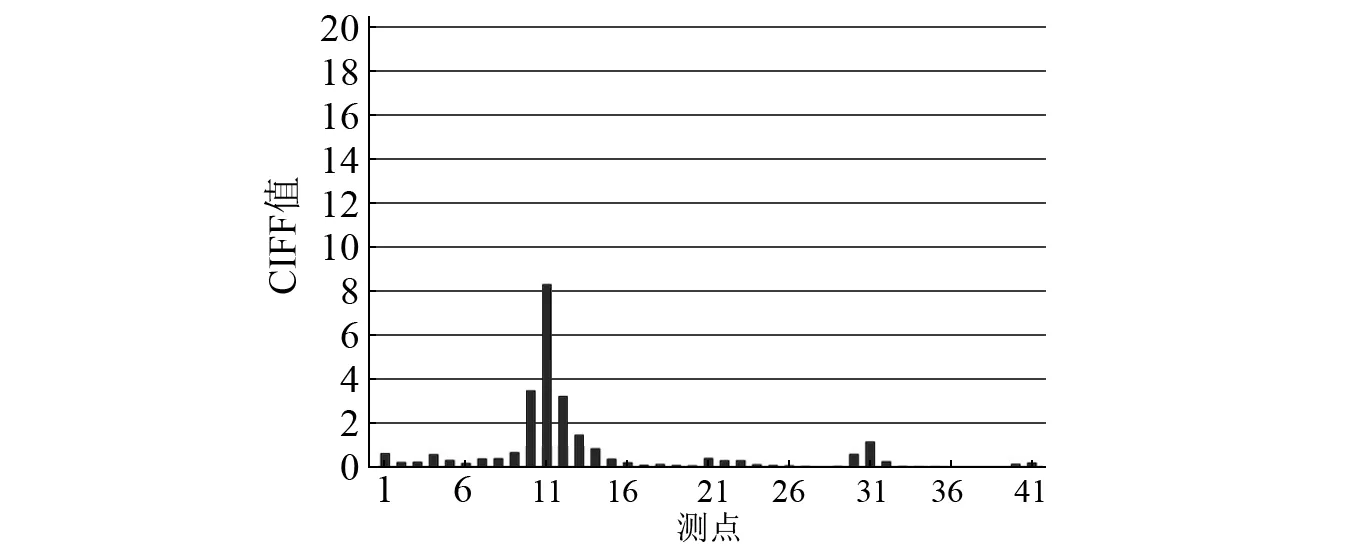
圖12 損傷一情況下各測點CIFF 值Fig.12 The amplitude of CIFF on first damage case

圖13 損傷一情況下各測點第一階 值Fig.13 The first order amplitude of on second damage case

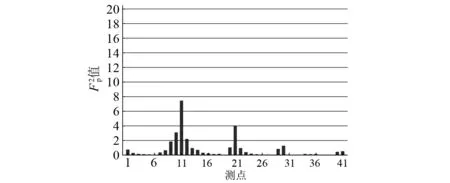
圖14 損傷二情況下各測點第二階 值Fig.14 The second order amplitude of on second damage case

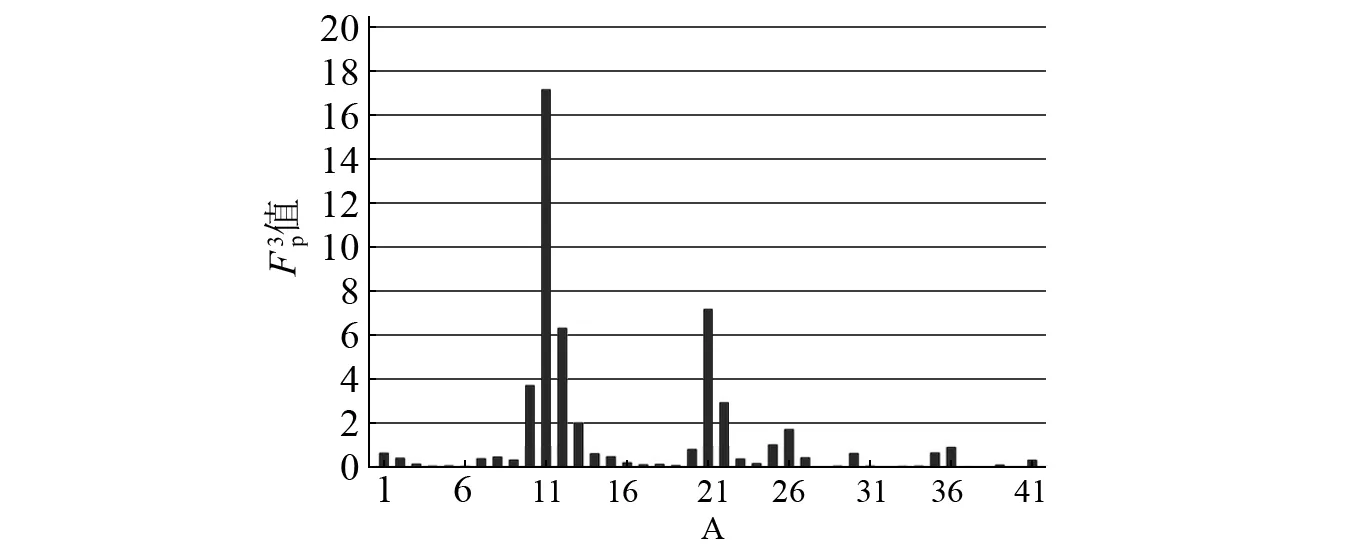
圖15 損傷二情況下各測點第三階 值Fig.15 The third order amplitude of on second damage case

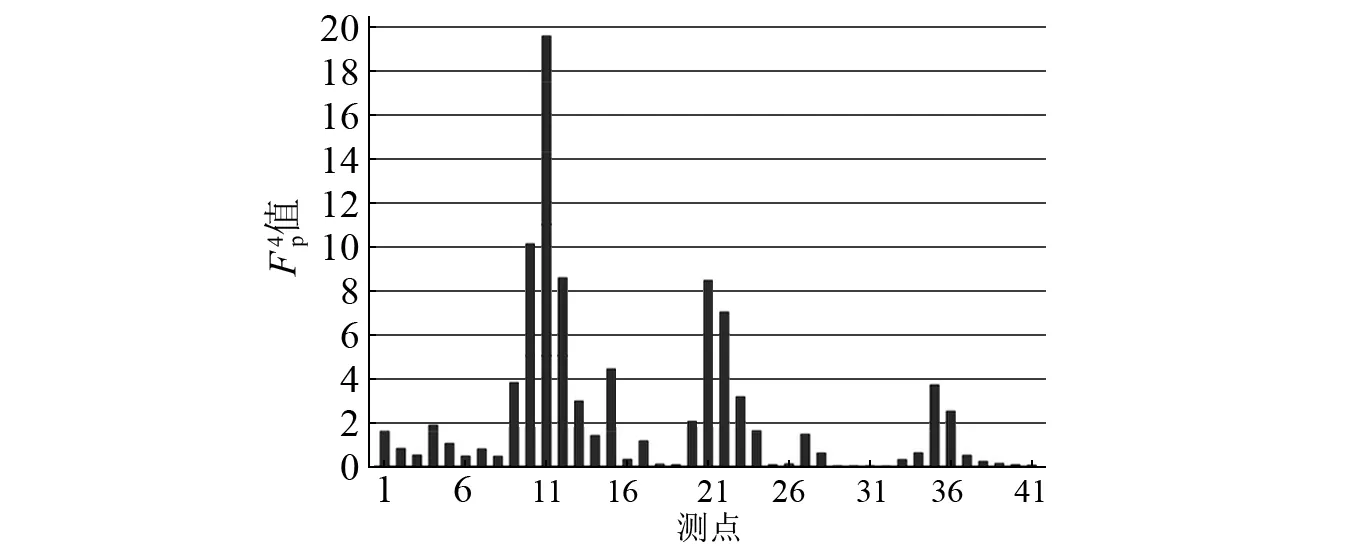
圖16 損傷二情況下各測點第四階 值Fig.16 The fourth order amplitude of on second damage case

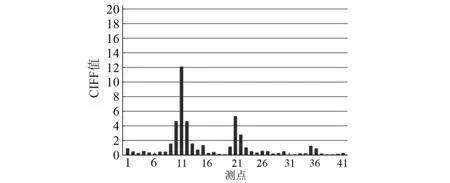
圖17 損傷二情況下各測點CIFF值Fig.17 The amplitude of CIFF on second damage case

4 結 論

本文提出了基于頻響函數虛部的梁結構損傷檢測法。通過頻響函數虛部振型曲率與平滑擬合曲率的差值構造出損傷判別因子CIFF，根據CIFF值出現的位置判定損傷出現的位置，并且可根據CIFF值的大小定性的判別損傷程度。通過一鋼質懸臂梁振動試驗，驗證了該方法對識別單損傷和多損傷的有效性。該方法僅需要求得結構損傷后的響應信息，避免了一些方法中需知道結構損傷前模態信息的弊端。并且試驗中選取的隨機荷載與工程測試中常用的環境激勵均為各態歷經的隨機過程，因此具有一定的工程應用價值。

[ 1 ] MODAK S V, KUNDRA T K, NAKRA B C. Comparative study of model updating methods using simulated experimental data[J].Computers and Structures, 2002, 80:437-447.

[ 2 ] ALVANDI A, CREMONA C. Assessment of vibration-based damage identification techniques[J].Journal of Sound and Vibration, 2006,292:179-202.

[ 3 ] FARRAR C R, LIEVEN N A J. Damage prognosis: the future of structural health monitoring[J].Philosophical Transactions of the Royal Society A, 2007,365:623-632.

[ 4 ] SHI Z Y, LAW S S. Structural damage localization from modal strain energy change [J].Journal of Sound and Vibration, 1998,218(5):825-844.

[ 5 ] PANDEY M B,SAMMAN M M. Damage detection from changes in curvature [J]. Journal of Sound and Vibration ,1991,145(2):321-332.

[ 6 ] 狄生奎, 鄧文婷, 王立憲, 等. 基于模態柔度改變率對系桿拱橋的損傷診斷[J]. 四川建筑科學研究, 2014(2):95-98.

DI Shengkui, DENG Wenting, WANG Lixian, et al. Damage identification of tied arch bridge based on modal flexibility index[J].Building Science Research of Sichuan, 2014(2): 95-98.

[ 7 ] 曹暉, FRISWELL M I. 基于摸態柔度曲率的損傷檢測方法[J]. 工程力學, 2006, 23(4): 33-38.

CAO Hui, FRISWELL M I. Nondestructive damage evaluation indicator based on modal flexibility curvature[J].Engineering Mechanics, 2006, 23(4): 33-38.

[ 8 ] WANG shanshan, REN Qingwen, QIAO pizhong. Structural damage detection using local damage factor [J]. Journal of Vibration and Control, 2006, 12(9):955-973.

[ 9 ] 張宇飛, 王山山, 甘水來. 基于隨機振動響應相干函數的梁結構損傷檢測法[J]. 振動與沖擊,2016, 35(11):146-150.

ZHANG Yufei, WANG Shanshan, GAN Shuilai. A beam’s damage detection base on coherence function of its random vibration response [J]. Journal of Vibration and Shock,2016, 35(11):146-150.

[10] LIU X, IIEVEN N A J, ESCANTILL-AMBROSIO P J. Frequency response function shape-based methods for structural damage localization[J].Mechanical Systems and Signal Processing, 2009, 23:1243-1259.

[11] 高海洋, 郭杏林, 吳明勇. 基于頻響函數虛部的板結構損傷檢測方法研究[J]. 振動與沖擊, 2012, 31(12): 86-91.

GAO Haiyang, GUO Xinglin, WU Mingyong. Damage detection for a plate based on imaginary part of frequency response function[J].Journal of Vibration and Shock, 2012, 31(12): 86-91.