載機大機動條件下空空導彈彈射發射動力學研究

劉 浩, 周 軍, 張士衛

(1.西北工業大學 航天學院，西安 710072；2.中國空空導彈研究院，河南 洛陽 471009)

隱身戰機(如美國F-22)一個新的標志性的作戰性能就是在圓周大機動高過載條件下實現空空導彈的彈射發射，對大機動高過載條件下的發射動力學特性進行研究具有重要的理論價值和工程應用價值。在現階段，相關文獻主要集中在載機平飛狀態條件下空空導彈的發射動力學研究[1-5]，在大機動高過載條件下的機載內埋彈射發射動力學研究還鮮見報道，相關研究文獻很少。陳全龍等[6]通過MSC /Dytran有限元分析軟件，建立飛機機體-導軌發射裝置-導彈系統的有限元模型，分析了在戰機典型飛行條件下和大機動條件下的導軌式發射方式的相關發射動力學特性，但還未涉及內埋彈射發射技術；許斌等[7]通過simulink軟件和adams軟件建立氣動式彈射發射系統的發射動力學模型，其重點在氣動彈射的驅動力數學模型研究，并未涉及載機大機動和機構柔性多體動力學效應。

針對目前隱身戰機大機動條件下內埋彈射發射動力學理論特性研究的嚴重不足，本文基于柔性多體動力學拉格朗日乘子法、構件級模態試驗和載機大機動條件，提出了一種隱身戰機大機動內埋彈射剛-柔-液耦合的動力學建模方法，該方法考慮了彈射發射裝置柔性機構大范圍高速運動、柔性變形以及液壓作動三者之間的耦合，最后通過數值模型仿真分析了大機動發射時的高過載離心力對發射動力學特性的影響，為隱身戰機大機動發射安全性研究以及空空導彈初始彈道研究提供理論依據。

1 大機動發射動力學模型建立

隱身戰機內埋彈射發射裝置采用高度輕量化設計思想，彈射速度高，彈射過載大，為了保證發射安全性對導彈分離參數的精度要求非常高。內埋發射裝置的彈射機構在大幅度的高速運動過程中柔性變形非常顯著，且在液壓作動耦合下其發射動力學特性更為復雜。多剛體動力學理論和運動-彈性動力學理論(Kineto-Elastodynamic Analysis, KED)已無法模擬其動力學特性。因此，本文采用剛-柔-液耦合動力學模型對大機動條件下的內埋彈射發射動力學特性進行研究。

1.1 載機大機動發射工況

隱身載機在進行圓周大機動時，將產生高過載離心力，該高過載離心力對導彈的彈射發射分離姿態將產生影響。圖1為戰機俯沖大機動彈射示意圖。導彈在彈射時受到的離心力：

Fg=mRω2

式中：m為導彈質量；R為大機動半徑；ω為大機動角速度。

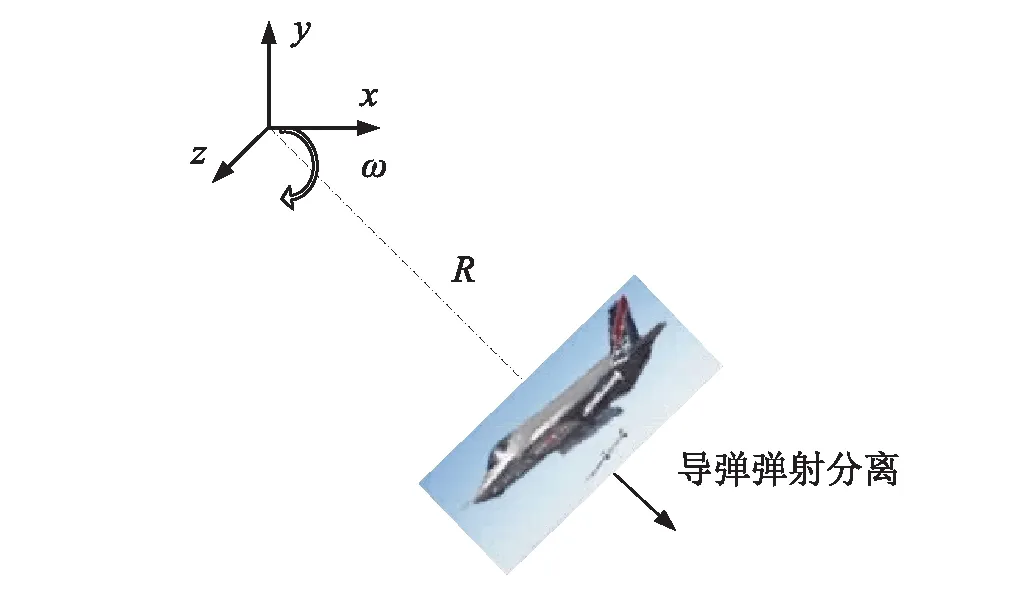
圖1 載機大機動彈射發射示意圖Fig.1 Launching under large maneuvering flight

1.2 內埋彈射發射裝置構型

以AMELT構型彈射發射裝置為研究仿真對象，其基本構型和構件連接關系如圖2所示。工作時，由液壓動力系統推動水平活塞及活塞桿向前滑動，由雙y字型機構將水平運動轉換成對導彈的豎直向下運動，最終實現導彈以良好的分離姿態與發射裝置彈射分離。

在仿真模型中，液壓動力缸和導彈作為剛體處理，上梁、水平活塞桿、各擺臂、各支臂均作為柔性體處理。

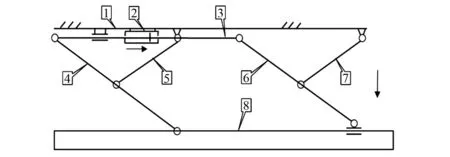
1.上梁；2.液壓動力缸；3.水平活塞桿；4.擺臂1；5.支臂1；6.擺臂2；7.支臂2；8.導彈。圖2 AMELT構型發射裝置結構示意圖Fig.2 AMELT configuration launcher

1.3 液壓缸彈射驅動力數學模型

隱身戰機內埋彈射發射裝置多采用氣液混合動力系統提供彈射動力(如美國F-22)，其基本原理是氣壓蓄能液壓傳動，從而實現彈射機構的高速作動。

1.3.1 蓄能器壓強數學模型

機載彈射發射系統作用時間短，約0.1 s，因此蓄能器采用理想氣體絕熱方程。

(1)

式中：p1為蓄能器初始壓強；v1為蓄能器初始氣腔體積；p2為蓄能器彈射過程中的壓強；v2為蓄能器彈射過程中的氣腔體積。

1.3.2 液壓閥門流量數學模型

閥口液壓流量數學模型：

(2)

式中：QL為流經閥口的液壓流量；cd為流量系數，一般取0.6；A閥口有效通徑面積；p3液壓缸內的壓強；ρ油液的密度，一般取900。

1.3.3 液壓作動缸壓強數學模型

在研究機構動力學時，文獻大多將液壓系統作為不可壓縮對象進行處理，但這與實際不符，尤其是在研究高壓快速作動的動力學模型時。本文考慮液壓的可壓縮性，認為液壓系統是依靠液壓體積的壓縮實現液壓壓強的建立，其壓強變化由以下公式建立：

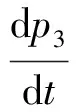
(3)

式中：QL為流經閥口的液壓流量；A1液壓缸有效作用面積；v彈射機構液壓活塞運動速度；VL進油腔體積；Eh油液的體積彈性模量，一般取700×106Pa；p3液壓缸內的壓強。

1.3.4 彈射機構液壓活塞加速度

彈射機構液壓活塞為整個彈射機構的運動驅動元件。液壓活塞在受到液壓壓強作用同時也輸出彈射作用力，從而推動整個柔性彈射機構高速運動。彈射機構液壓活塞的加速度方程為：

(4)

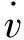
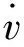
1.4 柔性多體動力學坐標系建立

在研究多柔體系統時，合適的坐標系是非常重要的。多柔體動力學研究一般采用慣性坐標系+浮動坐標系的方法[8-11]，該方法理論成熟、計算精度較高且便于數值計算。柔性體系統中的坐標系如圖3所示，包括慣性坐標系(er)和浮動坐標系(eb)。前者不隨時間而變化，后者是建立在柔性體上，隨著柔性體的變形而變化，該坐標用于描述柔性體的運動和變形。浮動坐標系可以相對慣性坐標系進行有限的移動和轉動。

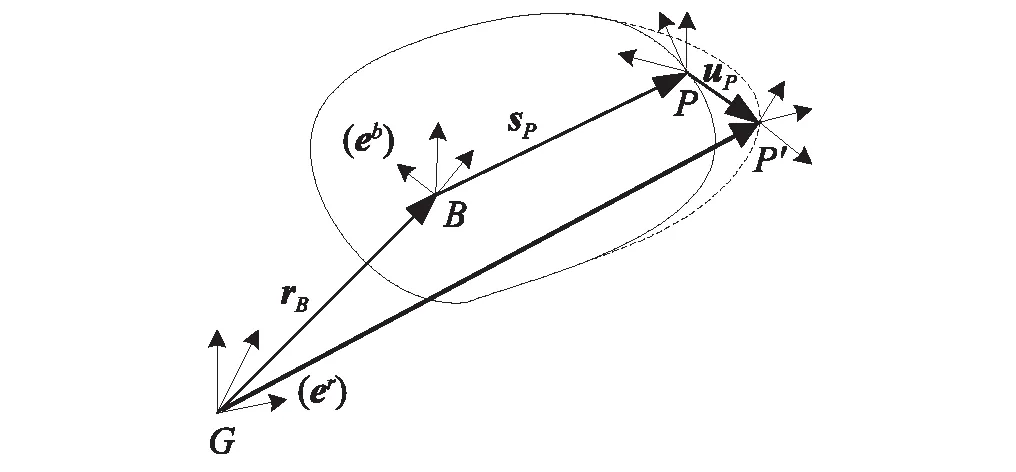
圖3 柔性體坐標系描述Fig.3 Flexible body coordinate system

1.5 柔性體上任意位置點運動描述

發射裝置柔性體上任意位置點p在絕對坐標系er下的運動可分解為相對絕對坐標系原點的剛性平動、剛性轉動以及相對于浮動坐標系的變形運動。質點p的位置運動可表述[10]為：

r=r0+A(sp+up)

式中：r為點p在慣性坐標系中的向量；r0為浮動坐標系原點在慣性坐標系中的向量；A為轉換矩陣；sp為柔性體未變形時p點在浮動坐標系中的向量；up為p點相對變形向量，up可以采用不同的方法進行離散化。本文采用模態坐標來描述，有：

up=Φpq

式中：Φp為模態矩陣；q為模態坐標。

發射裝置柔性體上任一點p的速度向量及加速度向量可以對r求對時間一階導數和二階導數得到：

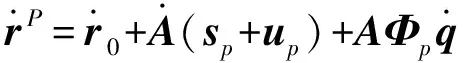
1.6 發射裝置多柔體動力學模型建立

1)動能T

考慮節點p變形前后的位置、方向和模態，柔性體的廣義坐標可以表示為：

ξ=[xyzψθφqi]T=[rψq]T, (i=1, 2, …,n)

系統的動能包括彈射裝置運動構件的動能和空空導彈的動能，表示為：

式中：質量矩陣M(ξ)為3×3維的方陣，表示為：

式中：下標t,r,m分別表示平動、旋轉和模態自由度。

2)勢能W

勢能分為彈射發射機構的重力勢能和變形產生的彈性勢能兩部分，可用下列二次項表示：

在彈性勢能中，K是對應于模態坐標q的結構部件的廣義剛度矩陣。重力勢能Wg表示為：

其中g表示重力加速度矢量，重力fg可對Wg求導得：

3)能量損耗

彈射機構彈射過載大，機構柔性變形顯著且迅速，其由阻尼力導致的能量損耗對機構的柔性變形需要考慮。能量損耗可由如下公式求得：

式中：D為阻尼系數矩陣。

4)多柔體動力學方程

多柔性體的運動方程從下列拉格朗日方程導出[12-13]：

式中：C為約束方程；λ為拉格朗日乘子；ξ為廣義坐標；Q為對ξ應的廣義力；L為拉格朗日項，定義為L=T-W；T和W分別表示動能和勢能。

最終的動力學微分方程為：

C=0

1.7 發射裝置構件自由模態試驗

機載內埋彈射發射裝置主要由三維形狀復雜的運動構件組成，在進行多柔體動力學仿真時采用模態法對各構件進行離散，為了提高各構件模態離散化精度，本文提出對數值模型中涉及到的主要構件進行自由模態試驗，通過模態試驗頻率和模態仿真頻率的對比，優化模態數值模型，為彈射發射裝置整機級數值仿真模型精度提供保障。

模態試驗時用橡皮繩將各構件懸吊，達到“自由-自由”的邊界條件狀態，在構件布置多個響應點并選擇好激勵點[14]。本文采用“猝發隨機”激勵方法，利用SCADAS 316系統QDAC模塊輸出激勵信號，響應測量采用單向加速度傳感器，采用SCADAS 316系統的PQFA模塊對所測數據進行采集。利用多參考最小二乘復頻域法(PolyMax)對所測數據進行分析處理，最后得到各構件的模態參數。圖4～圖6為內埋彈射發射裝置部分典型構件的模態試驗圖。

圖4 構件1 模態試驗圖Fig.4 Model test of part 1

圖5 構件2 模態試驗圖Fig.5 Model test of part 2

圖6 構件3 模態試驗圖Fig.6 Model test of part 3

從表1和表2中可以看出，模態仿真頻率和模態試驗頻率在1階和2階均具有相當高的精度，保障了發射動力學整機數值仿真模型的仿真精度。事實上試驗測試出的前3～5階模態頻率和仿真頻率均具有較高的匹配度。限于篇幅，本文對其他各階模態以及其他構件的模態不一一羅列對比。

表1 1階模態試驗與仿真頻率

表2 2階模態試驗與仿真頻率

2 發射動力學特性仿真分析

為了保持空優作戰性能，美國F-22能在8個過載的大機動條件下發射空空導彈，本文將仿真分析8個過載大機動條件下的高過載離心力對內埋彈射發射動力學特性的影響。

2.1 大機動對彈射分離參數影響特性分析

導彈彈射分離參數直接影響到隱身戰機的發射安全性和導彈的初始彈道。以下彈射分離參數均是相對于載機坐標系，即是空空導彈相對于戰機的分離參數。

圖7為導彈彈射分離速度曲線，如圖所示：在載機無機動發射時，彈射分離速度為8 m/s，分離時間為110 ms；在載機過載為4時發射導彈，彈射分離速度為9.1 m/s，分離時間為90 ms；當載機過載為8時，彈射分離速度為10.4 m/s，分離時間為77 ms。因此，隨著載機大機動時過載的增加，導彈彈射分離速度將明顯增加，分離時間將明顯縮短。

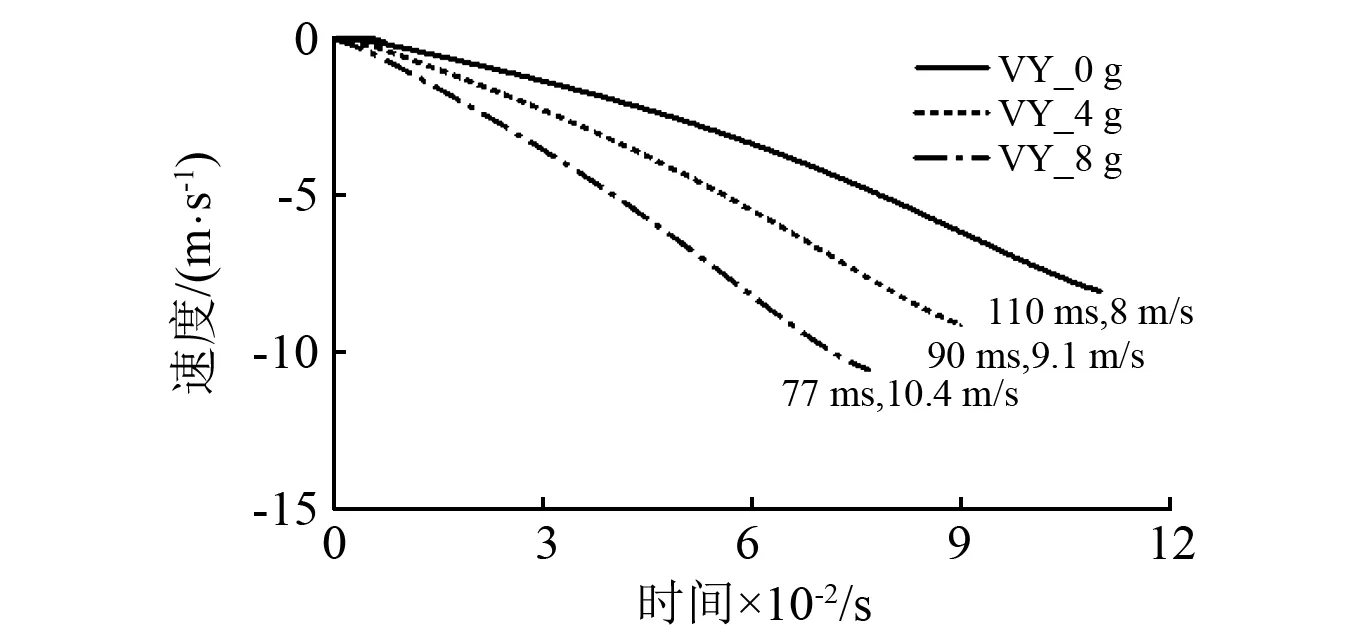
圖7 彈射分離速度曲線圖Fig.7 Eject separating velocity

原應分析：彈射時導彈受到載機大機動離心力作用，離心力對導彈作功，增加導彈彈射分離速度。彈射分離速度的增加將有利于導彈迅速穿越氣動干擾區域的影響，因此有利于發射安全性。

圖8為導彈彈射分離加速度曲線。從圖中可以看出在載機無機動發射時，彈射分離最大加速度為-105 m/s2；在載機過載為4時發射導彈，彈射分離最大加速度為-130 m/s2；當載機過載為8時，彈射分離最大加速度為-167 m/s2。彈射分離加速度的增加主要是由于導彈受到載機大機動圓周運動的離心力作用。彈射分離加速度的增加將有利于導彈迅速脫離載機，有利于發射安全性。

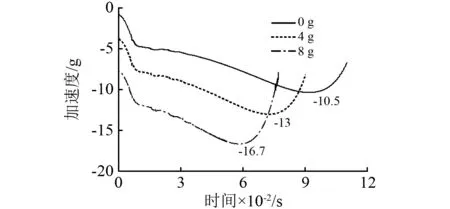
圖8 彈射分離加速度曲線圖Fig.8 Eject separating acceleration

圖9為導彈彈射分離角速度曲線，導彈發射時要求相對載機具有向下傾斜的低頭角速度，以保證載機的安全。從圖9中可以看出在載機無機動發射時，彈射分離低頭角速度為32.3°/s；在載機過載為4時發射導彈，彈射分離低頭角速度為30°/s；當載機過載為8時，彈射分離低頭角速度為26°/s。因此可以看出，戰機大機動高過載發射時，導彈彈射分離低頭角速度會出現一定程度的降低，降低約20%。

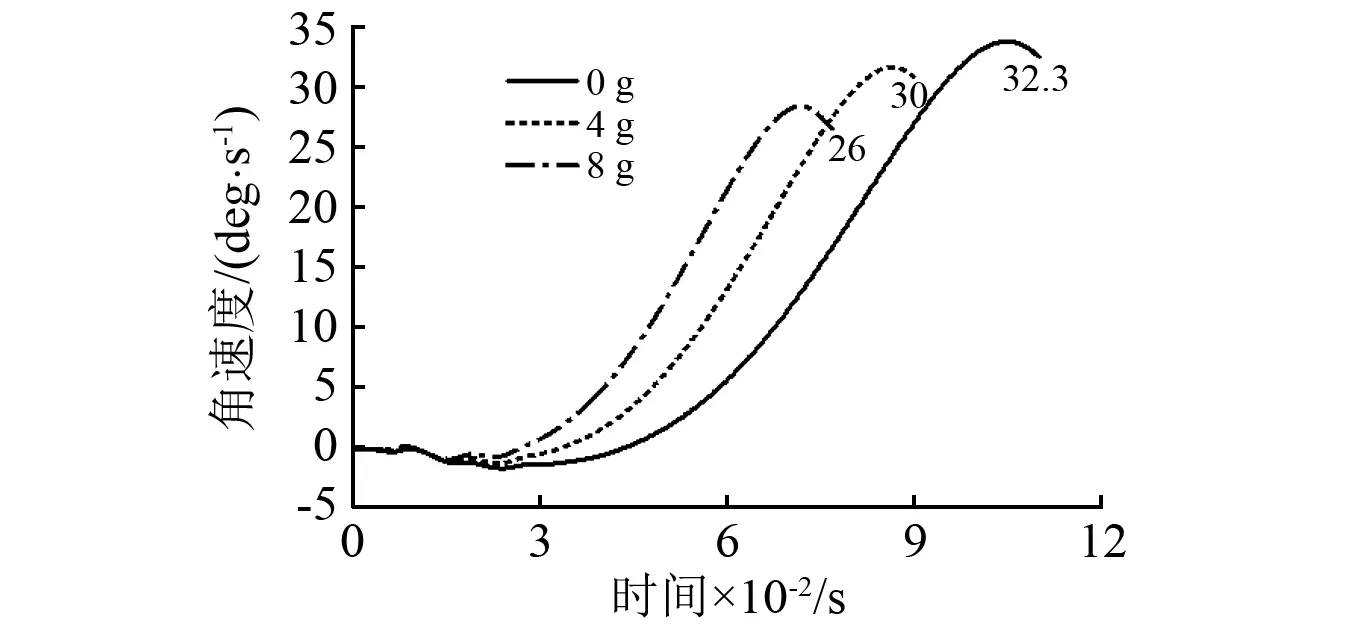
圖9 彈射分離角速度曲線圖Fig.9 Eject separating angle velocity

圖10為導彈彈射分離低頭角度曲線，導彈發射時要求相對載機具有向下傾斜的低頭角，以保證載機的安全。如圖所示：在載機無機動發射時，彈射分離低頭角度為1°；在載機過載為4時，彈射分離低頭角度為0.84°；在載機過載為8時，彈射分離低頭角度為0.7°。可以看出，戰機大機動高過載發射時，導彈分離角度會明顯減小，減小量達30%，威脅發射安全。為了保證發射安全性，在武器系統設計時對此應予以充分考慮。

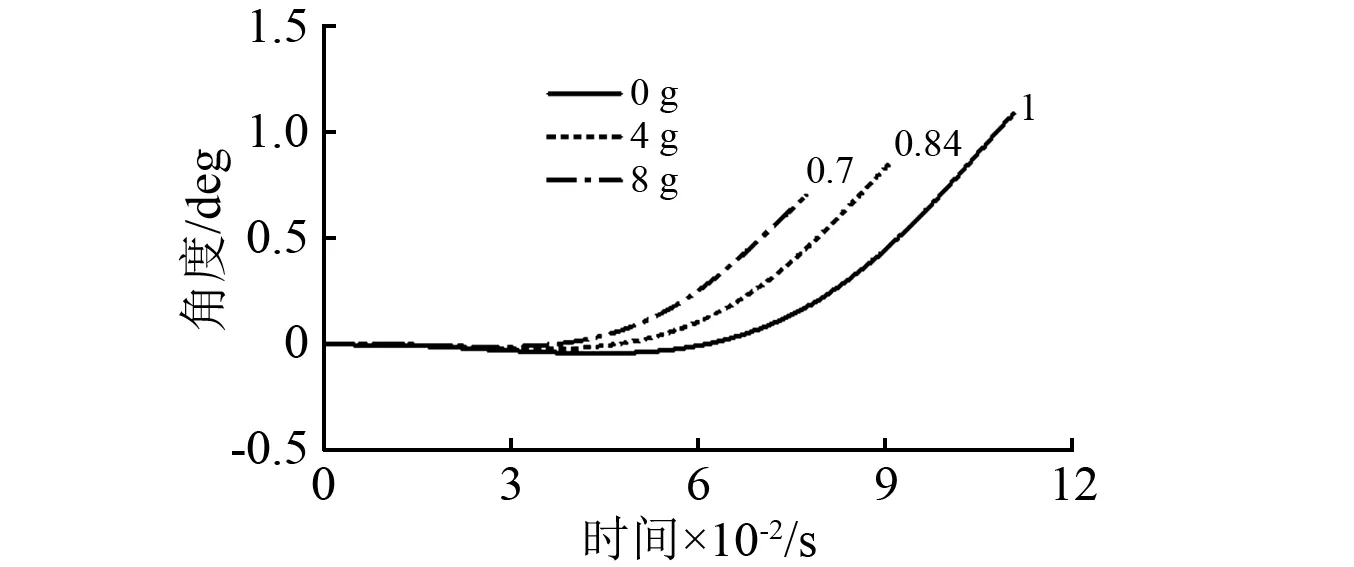
圖10 彈射分離角度曲線圖Fig.10 Eject separating angle

通過以上對彈射分離參數的仿真分析可以看出：載機作大機動高過載發射時，彈射分離速度和分離加速度將增加，有利于發射安全性；但是分離角速度和角度將不同程度的降低，對發射安全性將產生明顯影響，在武器系統設計時應予以充分重視。

2.2 大機動發射對結構強度設計影響研究

對導彈彈射分離過程中的戰機和導彈受力進行研究，包括載機所受的彈射反作用力和導彈所受的彈射作動力。該研究為載機和導彈的結構強度設計提供理論依據。

圖11為載機大梁與發射裝置機械接口的Y向受力曲線。導彈在彈射過程中，載機大梁接口受到向上的彈射反作用力，在導彈分離后，發射裝置各高速運動構件由于慣性將對載機大梁產生向下的拉力，直至在結構阻尼作用下趨于0。如圖所示：隨著大機動過載的增加，彈射過程中的反作用力峰值將降低，由16 000 N降低到14 500 N，在分離時，慣性產生的下拉力增加，由-5 800 N增加到-11 100 N。其原應在于：高過載離心力將加大導彈彈射分離速度，因此發射裝置構件的運動速度也將增加，在導彈彈射分離后的運動機構緩沖止動階段勢必增大對載機接口的慣性拉力。

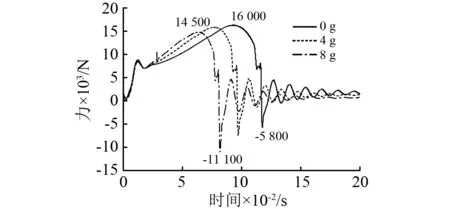
圖11 載機接口受力曲線圖Fig.11 Force of aircraft mechanical interface

圖12為導彈與發射裝置機械接口的Y向受力曲線。導彈在彈射過程中，導彈受到發射裝置的彈射作用力，在導彈分離后，導彈受到發射裝置的作用力為0。如圖所示：隨著載機大機動過載的增加，導彈所受彈射力基本不變。

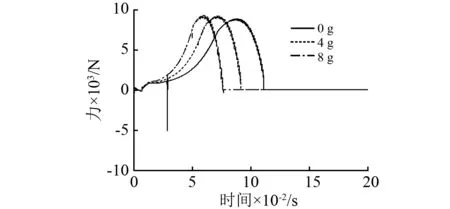
圖12 導彈接口受力曲線圖Fig.12 Force of missile mechanical interface

通過以上受力特性仿真分析可以看出：隨著載機大機動過載的增加，載機接口受到的彈射反作用力將降低，但是高速運動構件產生的止動慣性拉力將增加，載機結構強度設計時應予以考慮。導彈在載機高過載時受到發射裝置彈射作用力基本不變，不影響導彈強度安全設計。

3 結 論

針對隱身戰機在大機動條件下的彈射發射動力學特性研究的嚴重不足，且考慮到多剛體動力學理論和運動-彈性動力學理論無法模擬該動力學特性，本文提出了一種大機動條件下的內埋彈射發射剛-柔-液耦合動力學建模方法，并通過該模型對其發射動力學特性進行了數值模擬，為隱身戰機發射安全性和空空導彈初始彈道氣動研究提供理論依據。本文主要結論如下：

(1)本文提出的剛-柔-液耦合動力學建模方法能夠有效模擬隱身戰機的大機動內埋彈射發射動力學特性；

(2)本文提出的構件級自由模態試驗頻率與仿真頻率對比的方法能夠有效保證整機級數值模型的仿真精度；

(3)大機動發射時，導彈彈射分離速度和加速度將會明顯增加，有利于發射安全性；

(4)大機動發射時，導彈彈射分離低頭角速度和低頭角將會明顯降低，威脅發射安全性；

(5)大機動發射時，載機在彈射時所受的反作用力將減小，但導彈分離后載機受到的運動機構慣性拉力將增加，載機結構強度設計時應予以重視；

(6)大機動發射時，導彈所受的發射裝置彈射動力幾乎與平飛發射相當，導彈強度設計不受影響。

[ 1 ] 劉剛， 肖中云，王建濤，等. 考慮約束的機載導彈導軌發射數值模擬[J]. 空氣動力學學報，2015(2)： 52-57.

LIU Gang, XIAO Zhongyun, WANG Jiantao, et al. Numerical simulation of missile air-launching process under rail slideway constraints[J]. Acta Aerodynamica Sinica，2015(2)： 52-57.

[ 2 ] 王林鵬，王漢平，楊鳴，等. 運動導彈激勵下柔性導軌振動的多體動力學分析法[J].航空學報，2014(3)： 169-176.

WANG Linpeng, WANG Hanping, YANG Ming ,et al. Multi-body dynamics analysis method for vibration of flexible guide activated by moving missile[J]. Acta Aeronautica ET Astronautica Sinica，2014(3)： 169-176.

[ 3 ] 李克睛，譚浩，王瑞鳳. 導彈發射瞬時運動安全性分析[J]. 戰術導彈技術， 2014(2)： 28-33.

LI Kejing, TAN Hao, WANG Ruifeng. The safety analysis for processing of missile launch[J]. Tactical Missile Technology，2014(2)： 28-33.

[ 4 ] 王小鵬. 靜不穩定空空導彈導軌發射機彈分離數值模擬[J]. 計算力學學報， 2013，30(增刊1)： 22-24.

WANG Xiaopeng. Numerical simulation on separation for statically unstable air-to-air missile by rail launch[J]. Chinese Journal of Computational Mechanics，2013，30(Sup1)： 22-24.

[ 5 ] 廖莎莎，吳成. 機載導彈發射動力學建模與虛擬樣機仿真[J]. 北京理工大學學報， 2011(9)： 9-13.

LIAO Shasha， WU Cheng. Launching dynamics modeling of guided aircraft missile and virtual prototype simulation[J]. Transactions of Beijing Institute of Technology， 2011(9)：9-13.

[ 6 ] 陳全龍，韓景龍，員海瑋. 機載導彈導軌式發射過程安全性分析[J]. 振動與沖擊，2013， 32(20)： 41-47.

CHEN Quanlong, HAN Jinglong, YUN Haiwei. Security analysis of missile rail-launching from an aircraft[J]. Journal of Vibration and Shock， 2013， 32(20)： 41-47.

[ 7 ] 許斌， 楊積東， 劉廣， 等. 機載導彈彈射式發射建模與仿真[J]. 系統仿真學報， 2011， 23(7)： 51-54.

XU Bin, YANG Jidong, LIU Guang , et al. Modeling and simulation of eject launcher for airborne missile[J]. Journal of System Simulation， 2011， 23(7)： 51-54.

[ 8 ] LIKINS P W. Finite element append age equations for hybrid coordinate dynamic analysis [J].Journal of Solids and Structures， 1972(8)： 790-831.

[ 9 ] LIKINS P W. Spacecraft attitude dynamics and control a personal perspective on early develop -ments[ J]. Journal of Guidance and Control， 1986， 9(2): 129-134.

[10] 陸佑方.柔性多體系統動力學[M].北京:高等教育出版社， 1996.

[11] 黃文虎，邵成勛. 多柔體系統動力學[M].北京:科學出版社， 1996.

[12] CHEN Wen. Dynamic modeling of multi-link flexible robotic manipulators [J]. Computers and Structures， 2001 (9):183-195.

[13] 劉明治，劉春霞.柔性機械臂動力學建模和控制研究[J]. 力學進展， 2001, 31 (1): 1-8.

LIU Mingzhi, LIU Chunxia. The study on dynamics modeling and contorl of flexible mechnical arms[J]. Advances In Mechanics， 2001, 31 (1): 1-8.

[14] 何輝.多參考最小二乘復頻域法在飛行器模態參數識別中的應用[J]. 航空兵器，2010， 12(6): 7-11.

HE Hui. Applications of the polymax method in aerocrafts modal parameter estimation[J]. Aero Weaponry，2010， 12(6): 7-11.