一種應用于諧振式光纖陀螺的數字雙相位鎖相放大器的設計

張 焱,唐 杰,趙 寧,張 彤1,*

(1.東南大學儀器科學與工程學院,南京 210096;2.東南大學電子科學與工程學院,南京 210096;3.東南大學蘇州研究院蘇州金屬納米光電技術重點實驗室,江蘇 蘇州 215123)

陀螺是一種用于測量物體角速度和角位移的裝置,是慣性導航系統中的關鍵器件之一[1-3]。諧振式光纖陀螺具有光纖長度短、體積小、檢測精度高等特點,使其得到廣泛的研究,成為角速度慣性傳感領域重要發展方向[4-5]。諧振式光學陀螺的基本原理為光學Sagnac效應[6-7],由于Sagnac效應是一種非常微弱的效應,所以通過Sagnac效應轉換得到的電壓信號通常是納伏級別的,具有信號弱、噪聲強的特點,如此微弱的信號是無法進行提取的,因此微弱信號檢測電路設計為系統電路設計的一個重要的內容。鎖相放大器LIA(Lock-in Amplifier)是微弱信號的關鍵技術之一,它能夠改善系統的信噪比,提高檢測系統的性能[8-9]。本文設計了一種無需相位調整數字雙相位鎖相放大器,將微弱的陀螺信號從噪聲中檢測出來。目前應用于諧振式光纖陀螺的鎖相放大器主要有純模擬鎖相放大器、數模混合鎖相放大器和數字鎖相放大器[10-12]。相比于模擬鎖相放大器,數字鎖相放大器具有穩定性好、抗干擾能力強以及易于集成等特點,本文所提出的雙相位鎖相放大器以數字電路方式集成到FPGA上實現。數模混合鎖相放大器前端放大、整形、移相和濾波電路主要通過模擬電路實現,后端正交矢量計算通過數字電路實現,結構較為復雜。鎖相放大器的性能直接影響到陀螺的輸出精度,因此對鎖相放大器的研究具有重要意義。

1 諧振式光纖陀螺閉環鎖頻原理

諧振式光纖陀螺閉環鎖頻原理如圖1所示,激光光束(中心頻率為f0)經由相位調制器PM(Phase Modulator)調制后輸入光纖諧振腔。其中從諧振腔耦合出的光束,經光電探測器PD(Photodetector)輸出轉化為電壓信號[13-14]。隨后利用雙相位鎖相放大器的相關檢測原理對PD探測的電壓信號進行同步解調,輸出信號為激光器中心頻率f0與光纖諧振腔諧振頻率的差頻信號。將鎖相放大器的輸出做為PI控制器反饋信號,構建頻率伺服回路。伺服反饋將一直進行,直至激光器的中心頻率f0鎖定到諧振頻率上[15]。系統中,相位調制器PM采用正弦波調制信號對光束進行相位調制。

圖1 諧振式光纖陀螺閉環鎖頻原理圖

2 雙相位鎖相放大器的設計

鎖相放大器的原理框圖如圖2所示,主要包括4個部分:信號通道、參考通道、相敏檢測器和低通濾波器。

圖2 鎖相放大器原理框圖

設被測信號為

x(t)=Vr·cos(ω0t+θ)

(1)

參考信號輸入為

r(t)=Vs·cos(ω0t)

(2)

式中:ω0是待測信號的頻率,θ是待測信號與參考信號的相位差。PSD以參考信號為準,對待測信號進行相位檢測。PSD輸出為:

up(t)=x(t)·r(t)=Vr·cos(ω0t)·Vscos(ω0t+θ)=0.5Vr·Vs·cosθ+0.5·Vr·Vs·cos(2ω0t+θ)

(3)

經過相敏檢測后,式(3)變為和頻和差頻兩個分量,再經過低通濾波器,濾除掉和頻分量和頻帶之外的噪聲,得到的輸出結果為:

u0(t)=0.5Vs·Vrcosθ

(4)

可以看出鎖相放大器可以根據待測信號的幅度和初始相位,完成對待測信號的鑒幅作用。當θ等于0時,此時鎖相放大器的檢測靈敏度最大。通常由于檢測信號與參考信號具有相位差,因此需要不斷調節參考信號的初始相位。為此我們設計了雙相位的鎖相放大器,它能夠消除初始相位的影響,使得參考信號與待測信號達到相位匹配,且檢測靈敏度最大,提高了可操作性。雙相位鎖相放大器基本結構框圖如圖3所示。

圖3 雙相位鎖相放大器原理圖

被測信號分別與CORDIC算法模塊輸出的正余弦函數相乘[16],各自得到兩個差頻和和頻分量,分別進入低通濾波器輸出為兩個相位相反的直流分量0.5Acosθ和-0.5Asinθ。將直流分量進行平方相加再開方,最后得到被測信號的幅度信號0.5 A。實現對待測信號最大靈敏度的鑒幅。基于FPGA的雙相位鎖相放大器設計主要包括CORDIC正余弦信號、加法器、乘法器、開方模塊和低通濾波器。其中乘法器和開方器直接調用FPGA內部的集成IP核,設計實現方便簡單。

2.1 基于CORDIC算法的正弦信號發生器

正余弦函數的產生一般使用查表法、多項式展開法或者數學逼近法,但這些方法不能滿足精度、速度和簡單性的要求,在硬件電路上不易實現。CORDIC算法僅用移位和加法運算以產生正弦調制信號,適合FPGA實現。

CORDIC算法以坐標旋轉為基礎,將旋轉角度θ分為若干個連續的小偏轉角θi,通過不斷迭代的方式搖擺逼近目標旋轉角度來實現整個旋轉過程。其基本原理如圖4所示。

圖4 CORDIC算法原理示意圖

將XY平面上的點A(x1,y1)旋轉θ到點B(x2,y2),新向量的坐標為:

(5)

將上述方程組改成矩陣的形式,可得如下向量:

(6)

CORDIC算法將旋轉角度θ分為若干個小部分,每部分旋轉一小角度θi。單步旋轉定義為:

(7)

式中:提取公因式cosθi,可修改為:

(8)

選取每一次旋轉角度θ為正切值為2的指數,除以2的指數可以通過右移操作完成。每次旋轉的角度可以表示為:

(9)

所有迭代的累加值最后等于最終所需要的角度θ:

(10)

Si為+1或者-1,根據旋轉方向而定,順時針為-1,逆時針為+1。

余弦值可以通過預先計算而消除掉。

cosθi=cos[arctan(1/2i)]

(11)

將計算過程中所有的余弦值相乘,得到一個增益系數K。

(12)

由于K是常值我們可以忽略它,得到:

(13)

可以看出,CORDIC算法只剩下移位和加減法,非常適合FPGA內部實現。引入變量z,來追蹤累加的旋轉角度。

zi+1=zi-Siθi

(14)

在旋轉模式下,CORDIC算法每次迭代公式為:

(15)

在進行n次迭代后,可以得到:

(16)

通過設置初始值x0=1/k、y0=0和z0=θ,最終得到:

(17)

根據迭代公式,在FPGA內部采用16級流水線實現CORDIC算法,可以提高系統運算速率,獲得所需精度的正余弦調制波。根據上述原理,在FPGA內部編好相關代碼后,通過Modelsim仿真,得到的輸出仿真結果如圖5所示。

圖5 CORDIC算法仿真圖

由圖5可以看出,通過仿真成功得到了正弦與余弦曲線。

根據CORDIC算法,設置頻率控制字和相位控制字之后,在FPGA內部就能夠產生相應參數的正余弦波形。用頻譜分析儀對輸出波形進行頻譜分析,得到的結果如圖6所示。從圖6可以看出CORDIC模塊產生了800 kHz的正弦波,噪聲基底在-61.8 dBm以下,即信噪比達到了71.4 dB,得到的優良的正弦波信號,符合設計指標。

圖6 正弦信號頻譜分析圖

2.2 低通濾波器的設計

在鎖相解調模塊中,相敏檢測器的輸出信號為二倍頻交流分量和直流分量兩部分,低通濾波器濾除掉前者和系統中頻帶外噪聲,提高系統的信噪比,得到反映陀螺轉動的直流信號。因此低通濾波器的設計也是鎖相解調模塊的重要部分。

低通濾波器設計以一階無限脈沖響應IIR(Infinite Impulse Response)濾波器為基礎。圖7為低通濾波器的基本原理圖。

圖7 一階低通濾波器原理圖

根據圖7建立起的數字濾波環路的傳遞函數為:

(18)

式中:F為系統的時鐘頻率,系統的截止頻率為,通過設置K和F,可以得到符合設計指標的低通濾波器。根據式(18),設計截止頻率為1 kHz的低通濾波器,得到的幅頻響應曲線如圖8所示。其中紅色為仿真曲線,黑色點為實驗測試結果,可以看出實驗結果與理論分析基本吻合。

圖8 IIR濾波器幅頻響應曲線

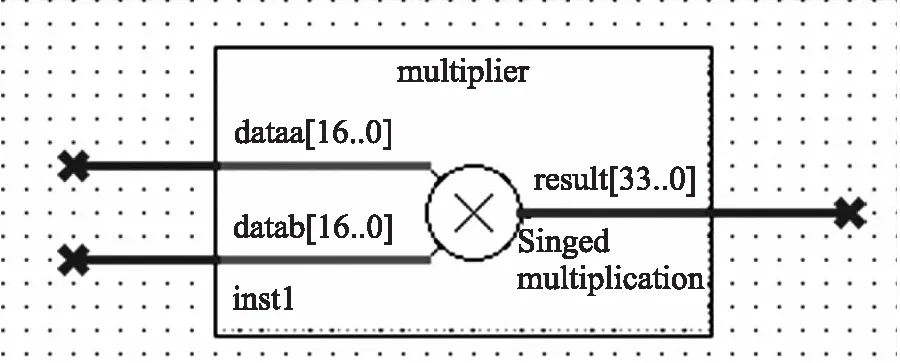
圖9 乘法器頂層原理圖

2.3 基于IP核的乘法器和開方器的設計

Altera在其開發集成環境中提供了IP核實例化和調用功能。本系統設計中采用了大量的IP核,包括乘法器和開方器。這些IP核大大的簡化了設計過程,縮短了開發周期。

如圖9和圖10分別為帶符號乘法器的頂層原理圖和Modelsim仿真圖。可以看出乘法器輸出無時鐘延遲,適合檢測系統高速設計的要求。

圖10 帶符號乘法器仿真圖

同樣對調用的IP核開方器在Modelsim上進行仿真,如圖11和圖12為開方模塊頂層原理圖和Modelsim仿真圖。

圖11 開方器頂層原理圖

圖12 開方器仿真圖

通過仿真結果可以看出調用的IP核乘法器和開方器的輸出符合邏輯功能設計,無系統延時,可以直接調用。

3 實驗與討論

對設計的鎖相放大器進行線性度測試,用信號發生器產生正弦波信號,經過ADC采集后送入FPGA內部,通過雙相位鎖定放大器探測,輸出為正弦波信號的幅度信息。輸入信號的幅度從50 mV增加到4 V,在Signaltap II內對鎖相放大器的輸出進行采樣保存,最后得到的鎖相放大器的線性度測試曲線如圖13所示。可以看出解調輸出基本上成一條直線,線性度良好。將小信號解調輸出放大,可以看到小信號解調輸出也基本成一條直線,線性度依然良好。

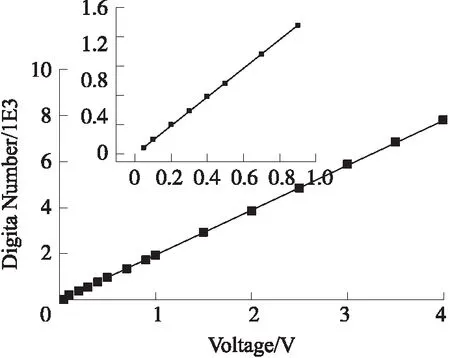
圖13 雙相位鎖定放大器線性度測試圖

如圖1所示搭建單路光纖諧振腔信號調制解調測試系統。用鋸齒波信號對激光器進行掃頻,可以測得光纖諧振腔的諧振譜線如圖14(a)所示。通過該譜線測得光纖諧振腔的自由譜寬FSR為112.5 MHz,半高全寬FMHW為2.7 MHz,清晰度為41.7。在FPGA內部采用CORDIC算法產生頻率為800 kHz,峰峰值為4Vpp的正弦信號給相位調制器對光波信號進行調制,并將光電探測器輸出的模擬信號通過DAC轉換為數字信號,送入在FPGA內部構建的雙相位鎖定放大器。鎖相放大器的參考信號為CORDIC算法產生的同頻的正弦波信號。通過雙相位鎖相放大器的解調得到的輸出曲線如圖14(b)所示,右上角局部放大圖中黑色曲線為鎖相輸出線性工作區間,紅色曲線為擬合曲線。通過擬合得到鎖相放大器輸出線性區間的線性度為0.999 77。結果表明,得到的解調曲線在諧振頻率處具有較高的線性度,這使得陀螺將具有較大的動態范圍和角速度測量精度。

圖14 光纖諧振腔掃頻曲線

4 結論

本文介紹了諧振式光纖陀螺鎖頻系統的原理,設計了一種無需相位調整的應用于諧振式光纖陀螺的雙相位鎖相放大器。與傳統的模擬鎖相放大器相比,該鎖相放大器采用數字電路實現,并集成到單片FPGA上,具有抗干擾能力強,易于調節等特點。通過該鎖相放大器解調,得到了高線性度的解調曲線。該線性區間為諧振式光纖陀螺的工作區間,因此可以獲得高線性度的陀螺輸出轉動信號,表明該鎖相放大器具有良好的性能。

[1] 郭秀中. 慣性系統陀螺儀理論[M]. 國防工業出版社,1996.

[2] Barbour N,Schmidt G. Inertial Sensor Technology Trends[J]. Sensors Journal IEEE,2001,1(4):332-339.

[3] Qian G,Tang J,Zhang X Y,et al. Low-Loss Polymer-Based Ring Resonator for Resonant Integrated Optical Gyroscopes[J]. Journal of Nanomaterials,2014,2014(3):119.

[4] Zhang T,Qian G,Wang Y Y,et al. Integrated Optical Gyroscope Using Active Long-Range Surface Plasmon-Polariton Waveguide Resonator[J]. Scientific Reports,2014,4(1):3855.

[5] Qian G,Fu X C,Zhang L J,et al. Hybrid Fiber Resonator Employing LRSPP Waveguide Coupler for Gyroscope[J]. Scientific Reports,2017,7:41146.

[6] Lee B. Review of the Present Status of Optical Fiber Sensors[J]. Optical Fiber Technology,2003,9(2):57-79.

[7] Culshaw B. The Optical Fibre Sagnac Interferometer:An Overview of its Principles and Applications[J]. Measurement Science and Technology,2005,17(1):R1.

[8] 劉順,李曉,王志斌,等. 基于彈光調制旋光測量的信號解調系統[J]. 傳感技術學報,2016,29(7):1021-1025.

[9] 陳浩,閆樹斌,鄭永秋,等. 應用于諧振式光纖陀螺的雙相位鎖相放大器的設計[J]. 儀表技術與傳感器,2014(11):93-95.

[10] 陳浩. 諧振式光學陀螺閉環鎖頻關鍵技術[D]. 太原:中北大學,2015.

[11] 樊天麒,劉巖,雷沖,等. 基于V/I轉換電路與鎖相放大器的磁阻抗測量系統簡[J]. 傳感技術學報,2016,29(10):1602-1605.

[12] 楊俊義. 基于FPGA的數字鎖相放大器研究[D]. 浙江大學,2012.

[13] Hong J B,Yeo Y B,Lee B W,et al. Phase Sensitive Detection for Mode-Locked Fiber Laser Gyroscope[J]. IEEE Photonics Technology Letters,1999,11(8):1030-1032.

[14] Zhi Y,Feng L,Lei M,et al. Low-Delay,High-Bandwidth Frequency-Locking Loop of Resonator Integrated Optic Gyro with Triangular Phase Modulation.[J]. Applied Optics,2013,52(33):8024-31.

[15] 閆樹斌,陳浩,鄭永秋,等. 諧振式光纖陀螺閉環鎖頻系統[J]. 紅外與激光工程,2014,43(12):4061-4065.

[16] Hu Y H. CORDIC-Based VLSI Architectures for Digital Signal Processing[J]. IEEE Signal Processing Magazine,1992,9(3):16-35.