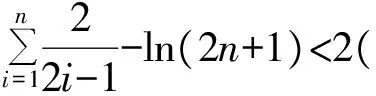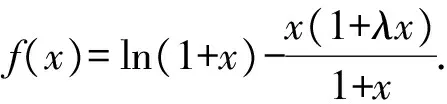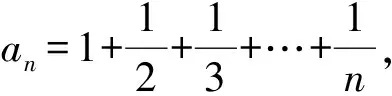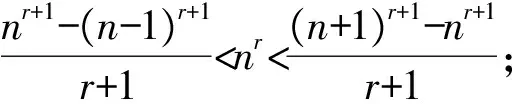從一道小學奧數題到高考壓軸題*
●
( 泉州第五中學城東校區,福建泉州362000)
1 緣起
自從女兒上了小學后,檢查作業、輔導功課成了幾年來每天晚上的必修課.個中滋味,家里誰有誰知道.本學期開學第一天晚上,便遇上了下面的例1,細思良久,方得解.被女兒狠狠嘲笑了一番,于是發奮圖強,進行了深入探究.
2 一道小學奧數題的解法探究
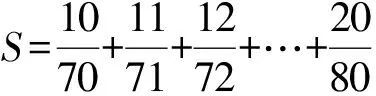
如何求解本題呢?
2.1 初數觀點下的解法探究
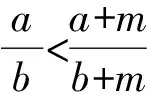

于是
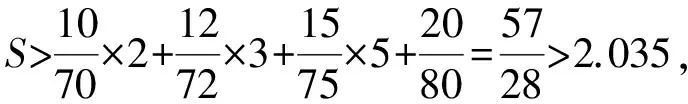
故2.035 筆者把題目曬在微信的朋友圈,各位好友踴躍互動,各路大神給出了各種建議,最后無非是解法1和下述的解法2. 即 因此 2.06 故S的整數部分為2. 筆者意識到此類數列求和問題往往可以通過積分中值定理進行放縮,于是拿起《數學分析》認真學習了一下,終于得到如下解法3. 則 f(n) 即 上述不等式累加得 f(10)+f(11)+…+f(20), 即 f(10)+f(11)+…f(20), 故 根據上述解法3的思路,即根據積分中值定理,我們可嘗試編制試題. 由于f(x)在(0,+∞)上單調遞增,從而 f(n) 即 (1) 因為50-ln 26≈46.741 9,50-ln 51≈46.068 2,所以 因此,可設置問題1: 為了給問題1設置解題的臺階,我們再來設置問題2. (2) 因此,筆者擬在問題2中設置與不等式“lnx 考慮引入參數,并包裝試題,增加題干隱蔽性,從而增加試題難度.設置問題2: 問題2[2]已知函數f(x)=xlnx-ax2+ax,且f(x)≤0,求實數a的值. 綜合上述兩個問題,成題如下: 例2已知函數f(x)=xlnx-ax2+ax,且f(x)≤0. 1)求實數a的值; (參考數據:ln 51≈3.931 8,ln 26≈3.258 1.) 尋尋覓覓,筆者在近幾年高考試題中尋得多個以此類手法命制的試題,呈現如下,與讀者共賞. 例3設函數f(x)=ln(1+x),g(x)=xf′(x),其中x≥0,f′(x)是f(x)的導函數. 1)令g1(x)=g(x),gn+1(x)=g(gn(x)),其中n∈N+,求gn(x)的表達式; 2)若f(x)≥ag(x)恒成立,求實數a的取值范圍; 3)設n∈N+,比較g(1)+g(2)+…+g(n)與n-f(n)的大小,并加以證明. (2014年陜西省數學高考理科試題第21題) 例4已知函數f(x)=x-ln(x+a)的最小值為0,其中a>0. 1)求a的值; 2)若對任意的x∈[0,+∞),有f(x)≤kx2成立,求實數k的最小值; (2012年天津市數學高考理科試題第20題) 1)若x≥0時,f(x)≤0,求λ的最小值; (2013年全國數學高考大綱卷理科試題第22題) 例6設n是正整數,r為正有理數. 1)求函數f(x)=(1+x)r+1-(r+1)x-1(其中x>-1)的最小值; 求「S?的值. (2013年湖北省數學高考理科試題第22題) [1] 中華人民共和國教育部.普通高中數學課程標準[M].北京:人民教育出版社,2003:2-3. [2] 崔紅光,楊蒼洲.例談試題的幾種編制方法[J].中小學數學,2016(11):63-64.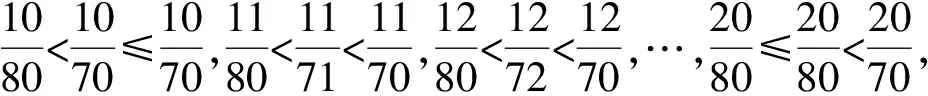
2.2 高數觀點下的解法探究
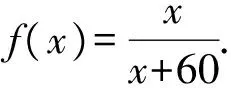

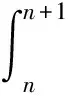
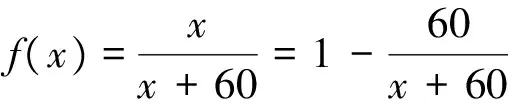
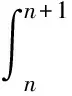
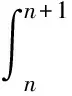
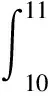
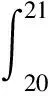

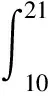

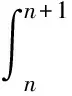
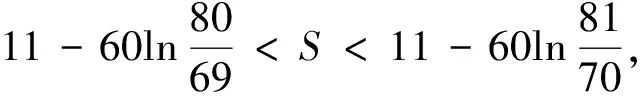
3 基于“積分中值定理”的試題命制
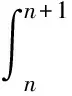
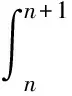
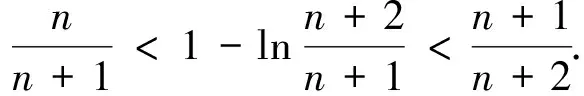
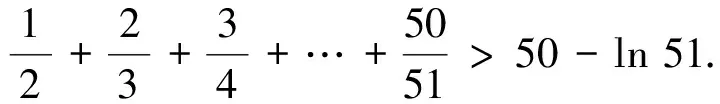
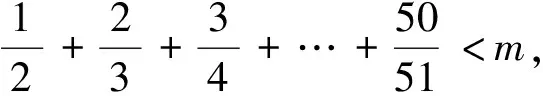
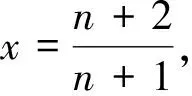
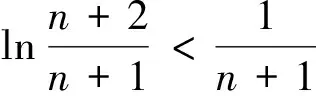
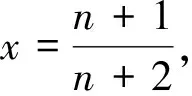
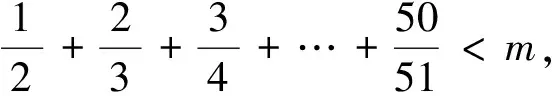
4 高考類題尋蹤