基于教師數學現場說題教研活動的思考與認識*

●

(南安市教師進修學校,福建 南安 362300)

1 國內外研究現狀綜述

1.1 國內研究現狀綜述

上世紀90年代，“說數學”就引起了國內教育界的高度關注.曹才翰先生和章建躍博士所著的《數學教育心理學》中提出：通過“說數學”的教學活動能有效實現“數學地交流”.2003年頒布的《普通高中數學課程標準》提出“提高數學表達和交流能力”的課程目標.直到21世紀，國內數學教育工作者把“說數學”研究擴大到實踐層面，不斷把“說數學”細化，從而出現了教師“說題”的教學活動.2011年出版的《義務教育數學課程標準》，提高了學生“說”的地位，更重視提升學生的數學應用能力，而開展學生說題教研活動是提升學生能力的實質性舉措之一.國際上對中學數學說題的研究較早就開始了，但發展不成熟，大多是一線教師零散經驗的積累和總結，未成體系.本文結合教研實踐，主要談談教師如何進行數學現場說題.

1.2 國外研究現狀綜述

對于說題，最早可以追溯到古希臘著名的哲學家蘇格拉底的“產婆術”教學法.他主要采用談話式、討論式、啟發式的教育方法，通過向學生提問，不斷揭露對方回答問題中的矛盾，引導學生總結出一般性的結論，它的本質是教師引導學生去“說”，在“說”的過程中提升認識(師生互動說).1989年的《加拿大數學課程標準》，第一次提出把“說數學”作為評課的標準;新加坡的《大綱》十分重視學生用語言表達數學的能力；俄羅斯的《大綱》則在描述培養學生習慣方面更加明確，要求學生無論是口頭交流還是書面交流都要清晰流暢;美國數學教師協會(NCTM)在2000年制定的《學校數學的原理和標準》中的學習原理指出：“學生應該以理解的方式學習數學，在自身經驗和原有知識的基礎上建構對新知識的理解.”因此，教學中需要讓學生說出自己的思維過程;法國的《數學教學大綱》提出要讓學生能夠“明確地表述”“使學生在書寫和口頭交流方面形成清楚的習慣”;日本的數學教學大綱中也要求學生能夠“數學地表示、表達”；此外，荷蘭、英國等國家的教學大綱或課程標準也都把學生能“說數學”作為一個重要目標.

2 相關概念及案例

在日常的教育教學中，我們經常會聽到這樣的交流：“某某同學講的這道題，比老師講得還明白”“某某同學某學科會講題，他這科的成績比其他學科就是高！”“你看，這組習題我在下面自己研究透了，給自己講明白了，上課的時候得心應手”.作為教研員，下校聽課調研時，經常看到有些教師上課滿堂灌、學生被動聽，花大量時間解題訓練，不注重調動學生的學習積極性，不關注或少關注學生的數學思維活動.

鑒于此，筆者所在單位組織了多次教師說題比賽，取得了一定的成效.現結合福建省南安市開展的說題比賽及教研實踐，對幾個相關概念進行界定.

2.1 數學說題

數學說題是指說題者在精心解題的基礎上，面對被說題者，在題目的知識內涵、能力要求、思想方法、拓展變式、反思總結等方面作出解說，以口頭表達為主，以數學思想方法為依據，以問題本身涉及的知識內涵為基礎的一種教學研究活動.簡單地說，“說題”就是把審題、分析、解答和回顧等思維過程按一定順序說出來的一種教研展示活動.

從說題主體來看，說題可分為教師說題、學生說題、教師和學生互動說題.

2.2 教師現場說題

教師通過“選題、做題、想題、改題、編題”等一系列活動，向同行、專家系統地概括自己對題目的理解、分析、解答和反思的思維過程，并按一定規律和順序表達出來，是一種深層次的備課.

教師說題主要包括如下4個環節：1)說“背景來源”，即試題來源于教材、中(高)考試題、經典試題或數學競賽試題改編等.2)說“試題立意”，即指明試題的考查目標、《考試說明》所對應的要求，具體考查哪些知識點、能力、思想.3)說試題解法:一方面說教師如何分析講解，如講題的基本方法，具體操作流程等；另一方面說如何指導學生作答，比如指導學生根據分值進行分點、分層作答，指導學生根據材料尋找采分點,指導學生養成相應的答題習慣.4)說“拓展引申”,即結合學情和考情說對試題的評價或改進、解題規律的推廣、試題的拓展及變式分析以及對今后命題趨勢的分析及方向預測.

1)求a,b；

2)證明：f(x)>1.

(2014年全國數學高考卷Ⅰ理科試題第21題)

本題為“福建省南安市2017年中學數學現場說題比賽”中，南安一中廖老師選取的說題試題.該教師從題目背景、解法初探、進一步探究、解法總結、試題拓展、解題反思等方面進行說題.第1)小題容易得到a=1,b=2.下面著重對第2)小題進行研究，截取其中典型的部分展示如下：

顯然此處的一階導函數有點復雜，是否繼續前行，得有一個判斷，否則很可能費時費力，沒有好的成效.我們認為，一階導數應該有4個理想的模式：①恒大于0或者恒小于0;②可求出具體零點;③有單調性(可直接觀察出或者二次導恒正或恒負)；④二階導函數可求出零點.而此處一階導數并沒有看到上述理想的4種狀態，顯然二次導(除去恒正的項ex-1,x2)再求導也沒利用價值(四階導數才恒正)，因此考慮放棄此方法.有些情況沒能看出有這4種理想狀態，但是照樣能解出題目，稱其為理想狀態，意思就是能理想最好，不理想也無妨，也能解題.

g(x)min>h(x)max.

g″(x)=ex(ex+e-2)+2ex>0,

故f(x)>1.

評注證法1是處理不等式恒成立問題常用的通法，也就是將不等式恒成立問題轉化為差函數最值問題.這里采用“設而不求”的方法處理，此種方法共需求導3次，難度不可謂不大.

將ex≥x+1中的x用x-1替換，可得ex-1≥x，從而

因此只要證不等式

即證

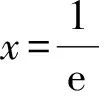
因為兩個不等式不能同時取到等號，所以

從壓軸題的多種證法出發，主要說解題思維的全過程、最常見的解法碰壁后如何處理(化歸)、學生解題經驗的積累運用等方面，目的是培養學優生善于發現轉化、歸納總結的能力，克服解決難題的心理畏懼感，深化學生思維，為成功拿下壓軸題奠定良好的知識儲備和心理基石.

3 說題的思考

3.1 說題的形式

3.1.1 一題一說

在教研活動中，不事先給說題者指定題目，由說題者根據自身需要，選擇所說的試題.說題者可查閱相關資料，認真學習相關理論，深刻研究試題所涵蓋數學知識的結構與分類，圍繞試題來源、考查目標、解法分析、拓展價值分析等方面進行充分準備，然后在教研活動現場向評委(專家)示說.

圖1

(2016年江蘇省數學高考試題第13題)

評注說題者可從試題的來源、解法探究(3種解法)、試題的推廣(簡單改編)、命題思路探尋、試題的實質性改造、教學啟示等方面進行說題[1].

3.1.2 一題多說

在教研活動中，組織者指定說題者針對同一習題(試題)，在同一次活動中展開示說.在活動中，教師可以展示自身教育理論功底、學科知識掌握程度、解題方法理解能力、對教學前瞻性理念的探求等，參與者能得到案例示范和理論滋養兩個方面的收益，營造良好的教研氛圍.學生在說題時，能展現其解答及思考過程，暴露對試題的思維過程.長期堅持說題，能提升其數學語言交流能力，培養學生敢于探索和創新的精神.

圖2

1)求甲、乙兩人奔跑t秒后，他們各自所處位置的坐標；

2)試問：甲、乙兩人出發后多長時間相距最近，最近距離為多少米？

(2011年福建省三明市質檢文科試題第21題)

評注對于本題，組織者可對說題者提出如下的說題要求:1)試題及解法展示；2)試題的評析(優、劣、存在的問題)；3)改編說明(主要闡述思路和理由)；4)改編題展示；5)改編題期望說明(主要考查目標，試題預設難度和區分度)；6)改編題的解法(以通性通法為主)；7)其他需要說明的問題.

比如對本題可以進行這樣的試題評析：本題以學生熟悉的足球場為背景，背景公正、合理，考查三角問題的實際應用，考查學生綜合分析問題和解決問題的能力;問題解決的過程中要求學生能利用圖形結合實際問題，建立坐標系，實現點的坐標化，體現了數形結合思想;利用兩點間距離公式，把最近距離問題化為二次函數的最小值問題，體現了化歸與轉化思想;存在的問題是試題中沒有指出甲在足球場的具體位置，t的范圍如何進行具體限制？

1)求甲、乙兩船航行4小時后，他們各自所處位置的坐標；

2)試問在第1)小題的條件下，如何確定乙船航行的方向使兩船此時距離最近，最近距離是多少？

改編說明把足球場改為海域，避免t的進一步限制，把行駛的時間設為定值，把乙行駛的方向角設置為變量，難度設置成“易”，使中等偏下的學生都能求解;第2)小題難度中等，使中等程度的學生能順利求解.改編后的試題環環相扣、梯度分明，較好地體現了試題的區分度，能有效區分出知識掌握程度不同的學生，體現“不同的人在數學上得到不同的發展”的理念.

3.1.3 多題一說

圖3

在教研活動中，說題者針對多道試題，就其共性方面(通解、數學思想方法等)展開示說.如圍繞以下4道高考試題可就“數形結合”思想來進行多題一說.

( )

(2009年遼寧省數學高考理科試題第8題)

說題1利用對稱性，由形到數.

( )

A.{3,4} B.{2,3,4}

C.{3,4,5} D.{2,3}

(2013年安徽省數學高考理科試題第8題)

圖4 圖5

說題2“由數思形”，建立對應關系.

例6若函數f(x)=x3+ax2+bx+c有極值點x1,x2，且f(x1)=x1，則關于x的方程3(f(x))2+2af(x)+b=0的不同實根個數是

( )

A.3 B.4 C.5 D.6

(2013年安徽省數學高考理科試題第10題)

說題3由數思形，以形助數.

由數思形：由極值點的意義可得x1,x2是方程3x2+2ax+b=0的兩個實根，再由該方程的結構特征(二次項系數為正)可得函數f(x)的單調性(先增后減再增)，從而可利用單調性作出該函數的草圖.因此要判斷方程3(f(x))2+2af(x)+b=0的不同實根個數，只需觀察直線y=x1,y=x2與函數f(x)圖像的交點個數情況(如圖6).以形助數：作出直線y=x1,y=x2以及函數f(x)的草圖即可得解.

圖6 圖7

例7設a∈R，若當x>0時，均有[(a-1)x-1](x2-ax-1)≥0,則a=______.

(2012年浙江省數學高考理科試題第17題)

說題4由數到形，數形結合.

按照常規思路，本題求解時通常可分為兩種情況：

受傳統經驗的影響，很多人可能會認為本題是錯題或解不出來.事實上，本題可先“由數到形”，即將所給含參不等式轉化成兩個函數值的符號相同問題，然后通過分別作圖(如圖7)，觀察它們的共同特征，“數形結合”得出它們的另一個交點位置是確定的，從而有效地避免了傳統解法的分類及繁雜的數學運算及推理，順利求出參數a的值.

4 結論

通過近幾年教師現場“說題”比賽的開展，筆者發現：教師在說題前進行的一系列準備工作，如查閱資料、理論學習、中(高)考試題研究等，有利于提高教師解題、命題水平，有利于提升教師的教研水平;在現場說題時，他們能充分展現自身數學教育的理論功底、數學知識的掌握程度、數學方法的理解能力及對數學本質的認識.通過多次教師現場說題比賽的開展，參賽教師能很快成為教改教研的骨干力量.

本課題研究開展一年以來，能充分調動各中學的積極性，課題組成員所在學校數學組教師開設片區級以上的展示課20多節，課題組成員所在學校教師和學生均取得了較好的成績.

[1] 陳俊斌.一道高考數學試題引發的探究與思考[J].數學通訊，2017(1)：30-33.