3D建模中的隨機(jī)之美謝作如

周源遠(yuǎn)

為現(xiàn)實(shí)生活的物品進(jìn)行3D建模，不僅要認(rèn)真測(cè)量實(shí)物，還要進(jìn)行各種比例計(jì)算，力求達(dá)到精確。但如果設(shè)計(jì)的是藝術(shù)品或者有藝術(shù)味的作品，又往往希望它能夠“隨性而為”。例如，讓某個(gè)作品模型每一次打印出來(lái)的實(shí)物都有一些不可預(yù)見(jiàn)的變化，是不是特別有意思？圖1中村莊的模型實(shí)際上用的是一個(gè)房子的模型，然后批量復(fù)制出來(lái)，這些房子的位置、大小和方向都是隨機(jī)生成的，整體上看起來(lái)錯(cuò)落有致。

在常見(jiàn)的建模軟件中，想要實(shí)現(xiàn)上述的想法并不容易，因?yàn)榇蠖鄶?shù)建模軟件沒(méi)有提供這樣的功能。幸運(yùn)的是，參數(shù)化建模軟件3D程序員提供了隨機(jī)數(shù)生成函數(shù)，使用者結(jié)合循環(huán)、縮放等語(yǔ)句，就能夠?qū)崿F(xiàn)在3D建模中加入隨機(jī)元素，讓生成的作品變得有趣。

計(jì)算機(jī)中的隨機(jī)數(shù)

在科學(xué)研究中常常用到隨機(jī)數(shù)，如從統(tǒng)計(jì)總體中抽取有代表性的樣本，或者將實(shí)驗(yàn)動(dòng)物分配到不同的試驗(yàn)組的過(guò)程中，或者在進(jìn)行蒙特卡羅模擬法計(jì)算的時(shí)候等。隨機(jī)數(shù)最重要的特性是，它所產(chǎn)生的后面的那個(gè)數(shù)與前面的那個(gè)數(shù)毫無(wú)關(guān)系。

在計(jì)算機(jī)編程中隨機(jī)數(shù)的應(yīng)用非常廣泛，最常見(jiàn)的是游戲和藝術(shù)繪圖。使用隨機(jī)數(shù)可以讓游戲產(chǎn)生不可預(yù)知的變化，從而增加樂(lè)趣。例如，“石頭剪刀布”游戲是電腦生成的一個(gè)隨機(jī)數(shù)和游戲用戶輸入的信息進(jìn)行比較。圖2是用Processing編寫(xiě)的小程序，功能是繪制出由隨機(jī)的點(diǎn)和線組成的圖案，每一次運(yùn)行都能產(chǎn)生不同的美麗圖案。

而真正意義的隨機(jī)數(shù)是按照實(shí)驗(yàn)過(guò)程中表現(xiàn)的分布概率隨機(jī)產(chǎn)生的，其結(jié)果是完全不可預(yù)測(cè)的。計(jì)算機(jī)生成的隨機(jī)數(shù)其實(shí)是“偽隨機(jī)數(shù)”，這些數(shù)列看上去“似乎”隨機(jī)，實(shí)際上是通過(guò)一個(gè)固定的、可以重復(fù)的計(jì)算方法產(chǎn)生的。即使這樣，計(jì)算機(jī)的隨機(jī)數(shù)也能夠滿足具體應(yīng)用中的大部分需求。

3D建模中隨機(jī)數(shù)的應(yīng)用

3D程序員的隨機(jī)數(shù)功能位于“數(shù)學(xué)”模塊，能夠生成起始值到終止值之間的整數(shù)。隨機(jī)數(shù)的具體應(yīng)用可以通過(guò)下面幾個(gè)案例來(lái)展開(kāi)。

案例1：隨機(jī)變化的花瓶

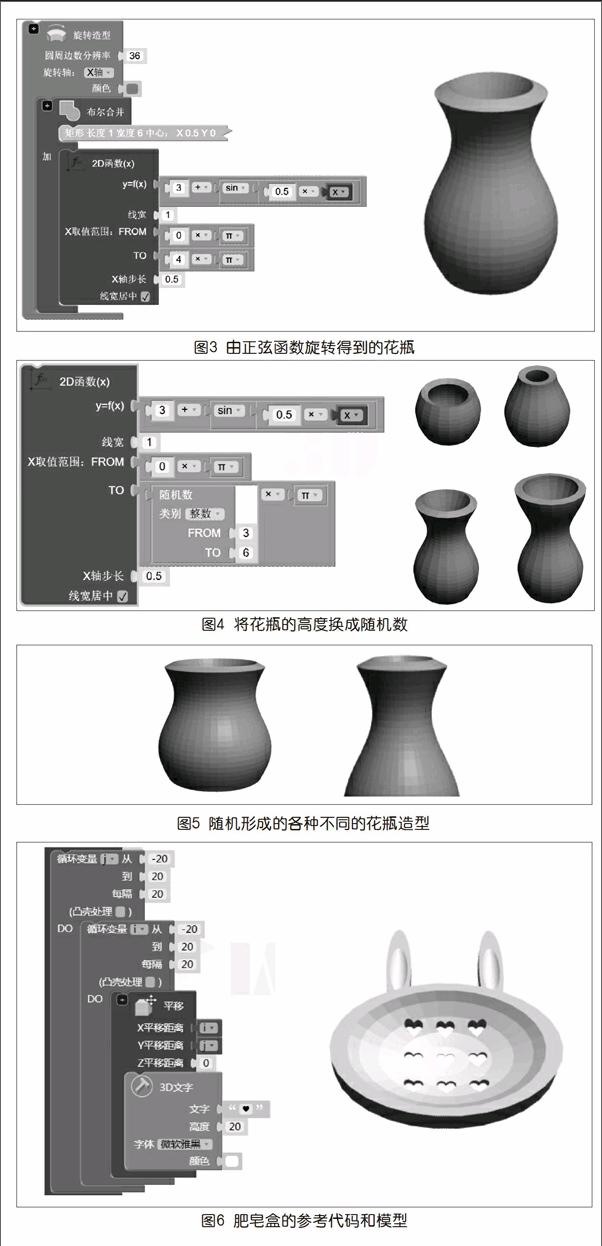
3D程序員中有個(gè)花瓶的范例，是典型的參數(shù)化建模例子。范例是描述利用一個(gè)正弦函數(shù)繪制的曲線，然后旋轉(zhuǎn)形成一個(gè)曲線圓滑而優(yōu)美的花瓶（如圖3）。

將正弦函數(shù)公式的一些關(guān)鍵參數(shù)替換為隨機(jī)數(shù)，就可以改變花瓶的整體長(zhǎng)度或者寬度，那么每一次產(chǎn)生的花瓶造型都會(huì)變得不一樣。圖4所示的是將花瓶高度換成隨機(jī)數(shù)的代碼，每一次生成的花瓶高度都是不一樣的。

同樣，也可以更改花瓶的寬度（如圖5）。這些造型不一的花瓶打印出來(lái)并擺在一起，能夠體現(xiàn)一種隨機(jī)之美。

案例2：隨機(jī)鏤空的肥皂盒

肥皂盒大都是由放置肥皂的凹處以及底盤(pán)的瀝水孔組成。設(shè)計(jì)一個(gè)肥皂盒，關(guān)鍵之處就是用循環(huán)語(yǔ)句來(lái)實(shí)現(xiàn)對(duì)瀝水孔的批量處理，這也可以用3D程序員實(shí)現(xiàn)。利用循環(huán)語(yǔ)句，用數(shù)學(xué)模塊指定循環(huán)變量i的起始值、終止值、每次循環(huán)的增量，參考代碼和生成的模型如圖6所示。

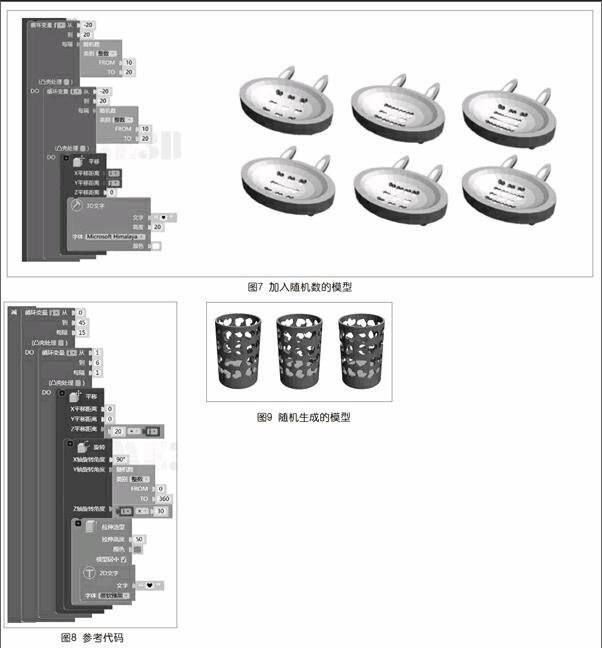
在循環(huán)的增量上加入隨機(jī)數(shù)，就能實(shí)現(xiàn)肥皂盒底下的穿孔數(shù)量隨機(jī)生成，而且每次生成的模型都不一樣（如下頁(yè)圖7）。

同樣，還可以在瀝水孔縮放系數(shù)上加入隨機(jī)數(shù)，讓瀝水孔的大小變得不一樣，甚至可以改變循環(huán)變量的起始值位置，讓瀝水孔的位置也發(fā)生變化。

案例3：隨機(jī)鏤空的筆筒

在循環(huán)的基礎(chǔ)上，以鏤空筆筒為例，角度旋轉(zhuǎn)結(jié)合隨機(jī)數(shù)，讓愛(ài)心的角度在0～360度內(nèi)隨機(jī)變化，生成多角度鏤空的愛(ài)心筆筒，這讓筆筒變得更有特色，參考代碼如圖8所示，效果如圖9所示。

這樣的案例還有很多。例如，構(gòu)造一棵圣誕樹(shù)，可以通過(guò)參數(shù)讓樹(shù)進(jìn)行“自由生長(zhǎng)”，隨機(jī)生成樹(shù)的分層次數(shù)或者葉片節(jié)點(diǎn)的數(shù)量。又如，設(shè)計(jì)一個(gè)創(chuàng)意童話城堡模型，可以用隨機(jī)數(shù)控制城堡的門(mén)、窗、煙囪等的大小，甚至可以通過(guò)隨機(jī)數(shù)在豐富的色域系統(tǒng)中隨機(jī)賦色。通過(guò)隨機(jī)數(shù)的應(yīng)用，建模將變得更有藝術(shù)性，跳出了傳統(tǒng)的基于精確計(jì)算的建模思維。

結(jié)語(yǔ)

在學(xué)習(xí)3D建模的過(guò)程中，無(wú)論是學(xué)習(xí)范例，還是最終設(shè)計(jì)自己的個(gè)性化作品，都在不斷重復(fù)經(jīng)歷提出問(wèn)題、選擇建模方法、推導(dǎo)模型的公式、求解模型這一建模過(guò)程，而隨機(jī)數(shù)的加入則從數(shù)學(xué)角度提出了更高的要求。因?yàn)橐侠硎褂秒S機(jī)數(shù)，就要找出模型的特征參數(shù)并設(shè)定合理的隨機(jī)數(shù)范圍，還要找出不同參數(shù)之間的關(guān)系，這些都是數(shù)學(xué)建模的核心能力。也正因?yàn)檫@樣，學(xué)生才有可能會(huì)為了設(shè)計(jì)出更加有趣的作品，認(rèn)真學(xué)習(xí)數(shù)學(xué)。通過(guò)“造物”促使學(xué)生進(jìn)行跨學(xué)科學(xué)習(xí)，并對(duì)學(xué)科更加感興趣，這正是創(chuàng)客教育的最大價(jià)值所在。endprint