圓錐曲線中與切線長相關的一組等式

江蘇省常州高級中學 (213003)

陳 武

圓錐曲線中與切線長相關的一組等式

江蘇省常州高級中學 (213003)

陳 武

文[1]把圓的切線長公式推廣到有心圓錐曲線中.

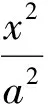
文[2]對于雙曲線的情形作出了更正與證明.

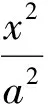
從公式中感受數學對稱美、簡潔美的同時，我們也自然地提出兩個問題：有心圓錐曲線中是否還存在與切線長相關的其他等式；拋物線中是否也存在與切線長相關的等式.

經過探究，筆者得到以下一組與切線長相關的優美等式.

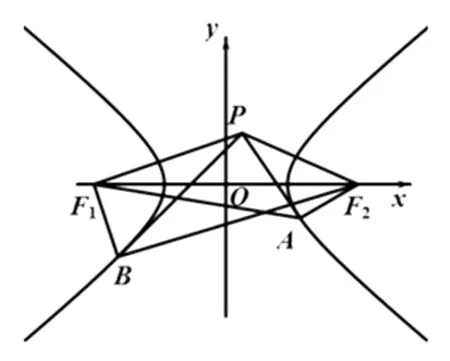
圖1

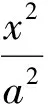
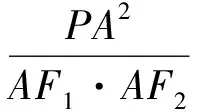
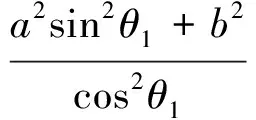
橢圓也有類似的性質，證明方法與性質1類似，不再另證.

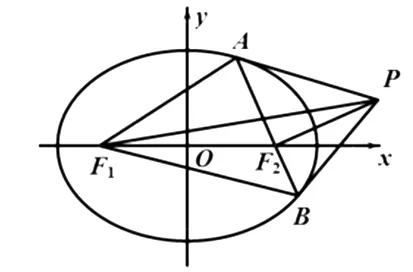
圖2

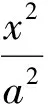
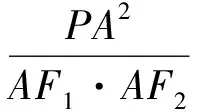
注:圓本質上是橢圓的一種退化形式(即橢圓的兩個焦點重合而成圓心),因此令a=b=r,(1)式變為PA2=x20+y20-r2,這就是圓的切線長公式.

性質5 如圖3，F為拋物線y2=2px(p>0)的焦點，過拋物線外一點P(x0,y0)作拋物線的切線，切點為A、B,則

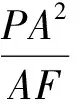
(2)PF2=AF·BF.

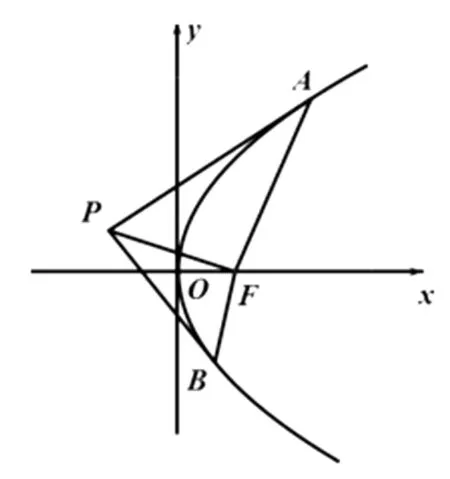
圖3

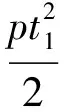
[1]徐文春.圓的切線長公式在有心圓錐曲線中的推廣[J].數學通訊(下半月)，2014(9):43-44.

[2]陳海波.有心圓錐曲線的切線長公式的更正及證明[J].數學通訊(下半月)，2015(5):61-63.