基于EFDC模型的青龍湖1號湖水體置換方案研究

申 超, 王勇波, 覃春喬

(中國電建集團成都勘測設計研究院有限公司， 四川 成都 610072)

基于EFDC模型的青龍湖1號湖水體置換方案研究

申 超, 王勇波, 覃春喬

(中國電建集團成都勘測設計研究院有限公司， 四川 成都 610072)

青龍湖是成都市重點規劃的城市景觀湖泊，由于水動力不足，湖水基本不動，水體易處于惡化狀態，需要通過人工換水保證水體質量。針對現有水體置換方案，利用環境流體力學模型(EFDC模型)建立了青龍湖1號湖的三維非穩態水量、水齡、污染物顆粒追蹤數學模型，對1號湖水體置換方案進行了模擬。模擬結果表明，風向對湖泊的水動力條件具有較大的影響：西北風的作用下引水對青龍湖1號湖的水動力改善最明顯，而在西南風的作用下引水對1號湖的水動力改善情況則不甚理想。不同的風向對1號湖水齡的改善情況不同，東北風有利于湖泊東北區域水齡的減小，東南風有利于西南沿岸區域水齡的減小，西北風有利于湖心區水齡減小，西南風有利于湖區西北部水齡的減小。同時，在成都市主導風向的條件下，風速的增加會使湖泊的水動力條件得到改善，但換水周期并不會隨著風速和流速的增加而減小。

EFDC模型； 青龍湖水體置換; 置換方案

1 研究背景

城市水面率是水生態文明建設的主要考核指標，目前已成為城市規劃和景觀設計的重要考量。城市人工湖泊作為形成城市水面的重要手段，具有良好的景觀、生態和文化效應，可極大提高湖泊周邊土地的利用價值，有力推動城市周邊經濟的發展。但是城市湖泊人工設計不夠科學，如:為滿足人們的景觀需求，多將湖岸設計成不規則形狀，曲折多彎，易出現湖泊水體的“死角”，“死角”中水體流動性較差，得不到置換，隨著使用時期延長，各種污染物發生沉積，最終導致水質惡化，并擴散到整個湖泊范圍；“死角”越多，所占范圍越大，水質惡化也就越快，達不到改善周邊環境和人文景觀的總體效果。青龍湖作為成都市東部新區的重要組成部分，是整個新區的生態基調確立區，并位于區內的腹心地區。然而，人工湖泊形成后，原本流動的水體變為靜止狀態，水環境質量難以維持。為保證湖體水質，青龍湖采用利用東風渠水源定期換水的方式進行水質保障，以保證水體的景觀效應得到最大限度的保障和提升。但是，傳統的水體置換理論只是通過簡單的計算庫容和出入庫流量來分析換水效果，而湖泊的水動力條件具有復雜多變的特性，很難保證每次換水都將所有水體進行一次完整的“置換”，因此,需要對換水效果進行進一步的計算分析。近年來，采用數值模型的方法分析人工湖體水體置換方案逐漸被廣泛重視。

目前，在河流、湖泊水質水動力研究中應用較為成熟的數值模型主要有EFDC、MIKE和WASP等。采用相關模型輔助具體河湖工程的生產設計已有較多應用，如:郝文彬等[1-2]應用MIKE和EFDC模型對湖泊和河流進行了數值模擬，為完善相關河湖的綜合治理提供了科學參考，取得了較好的應用效果。本文應用EFDC水質水動力綜合模型模擬了成都市青龍湖1號湖的湖泊流場，通過分析不同風向和風速條件下湖泊水動力條件與水齡分布與變化趨勢的影響，分析了調水方案的合理性，為人工湖的生態設計和調度提供了理論依據。

1.1 EFDC模型簡介及其基本原理

EFDC是由美國維吉尼亞海洋研究所根據多個數學模型集成開發研制的綜合模型，被用于模擬水系統一維、二維和三維流場、物質輸運(包括溫度、鹽度和泥沙輸運)、生態過程及淡水入流等[3]。

EFDC模型垂向上采用σ坐標變換，能較好地擬和近岸復雜岸線和地形[4]。采用修正的Mellor-Yamada2.5階湍封閉模式較客觀地提供垂向混合系數[5]，避免人為選取造成的誤差。其動量方程、連續方程及狀態方程如下。

動量方程為：

?t(mHu)+?x(myHuu)+?y(mxHvu)+
?z(mwu)-(mf+v?xmy-u?ymx)Hv=
-myH?x(gζ+p)-my(?xh-z?xH)?zp+
?z(mH-1Av?zu)+Qu

(1)

?t(mHv)+?x(myHuv)+?y(mxHvv)+
?z(mwv)+(mf+v?xmy-u?ymx)Hu=
-mxH?y(gζ+p)-mx(?yh-
z?yH)?xp+?z(mH-1Av?zv)+Qv

(2)

連續方程：

(3)

?t(mζ)+?x(myHu)+?y(mxHv)+?z(mw)=0

(4)

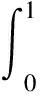
(5)

狀態方程ρ=ρ(P,S,T)

(6)

式中u、v、w——分別為邊界擬合正交曲線坐標x、y、z方向上的速度分量;

mx、my——分別為水平坐標轉換因子;

m=mxmy——為度量張量行列式的平方根;

Av——為垂向上的紊動粘滯系數;

Ab——為垂向上的紊動擴散系數;

f——為科里奧利系數；

P——為壓力;

ρ——為流體混合密度;

ρ0——為參考密度;

S——為鹽度;

T——為溫度;

Qu、Qv——為動量的源匯項。

1.2 水 齡

水齡是指某一區域水體被交換所需要的時間，水齡根據示蹤劑來計算，該概念類似于水力停留時間，可用于反映計算區任一網格的水體交換快慢[6]。計算公式如下：

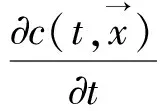
(7)

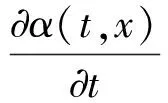
(8)

式中t——為時間；

c——為示蹤劑濃度；

u——為時空分布的流速；

K——為擴散張量；

α——為水齡密度。

可計算出平均值為：

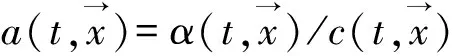
(9)

水齡定義為顆粒物從入口傳輸到定點的時間(往往入口的水齡最小)。水齡越大說明水體運動越慢，水體被交換程度越弱；反之亦然。

1.3 研究區域概況

青龍湖水庫工程位于龍泉驛區的十陵街道(見圖1)，工程包括已建青龍湖，擴建青龍湖1號湖、2號湖，以及濕地工程。擴建1號湖水體總容積168萬m3，工程屬Ⅳ等小(1)型湖，主要建筑物包括擋水壩、進水閘、排水閘、排洪渠，次要建筑物包括湖岸護岸、南五支渠改道灌溉渠工程等。

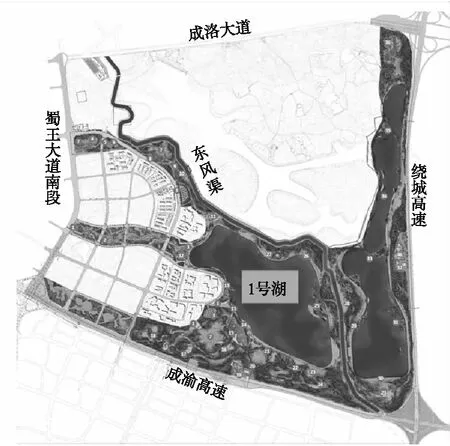
圖1 青龍湖1號湖示意

青龍水庫工程位于成都市東部淺丘臺地區，由于受到西風南支急流及印度洋、太平洋季風氣流的交替影響，加上西部高原及北部秦嶺的屏障作用，氣候四季分明，具有冬暖、春旱、夏熱、溫差大、云霧多、日照少、秋季多綿雨等氣候特點，屬副熱帶季風氣候。

根據青龍水庫工程設計，擴建1號湖采用新建充水閘從東風渠取水充蓄湖區， 1號湖設計蓄水位511.50 m，正常蓄水位以下水體容量119萬m3。

2 水動力模型的建立

2.1 青龍湖1號湖水動力模型的構建

用笛卡爾直角坐標系建立青龍湖1號湖水動力模型，共有網格數7 882個，每個網格單元邊長相當于實際長度10 m，為了較好地模擬湖底地形，垂直方向采用σ坐標。用湖底和表層水體厚度來定義垂向高度，每個網格的初始平均水深從岸邊的0.5 m到湖中心的3 m，見圖2。

根據流體靜力學連續性和避免產生σ坐標帶來的壓力誤差梯度錯誤，應使湖底坡度小于0.33 m。以出入湖流量和表面風力作為邊界條件，入湖流量采用設計換水流量1.5 m3/s，為保持湖體水量平衡，南五支渠出湖流量也設置為1.5 m3/s。表面風速采用湖泊風生流最低啟動流速5 m/s。在假設湖面水平的條件下初始水位設置為511.5 m，初始流速設置為0 m/s，模型采用穩定的邊界條件和初始條件，時間步長為3 s。

2.2 模型參數的確定

模型參數的選取對模型結果的影響十分重要。由于水流運動的理論已十分成熟，在EFDC模型的應用中大部分參數均未改變。在水位的率定過程中，通常需要調整的參數是底部粗糙高度Z0，該值一般取0.02 m[7]。本文研究中該參數的默認值也是0.02 m。研究表明[8]粗糙高度的變化對模型運行結果中的流速和水深造成的影響可忽略(水面高程和流速均方根誤差小于1%)。湖泊的水深主要受降雨、風場、支流的影響。

2.3 計算方案

淺水湖泊的水動力條件主要受風場、支流的影響。由于青龍湖1號湖平均水深1.8 m，是典型的淺水型城市人工景觀湖泊，除出、入湖泊的東風渠支渠和南支渠外，無另外的進出支流(見圖3)。因此，青龍湖1號湖水動力的主要影響因素為出入湖兩條河道及風場條件，故本次計算主要考慮進出湖流量及風場條件對湖泊水動力條件的影響。通過模擬試算各方案青龍湖流場、水齡和示蹤劑濃度可知，青龍湖流場、水齡和示蹤劑濃度一般計算在7 d后達到穩定，為確保計算的穩定性和結果的代表性，選取最后1d的結果進行分析計算，方案如表1所示。

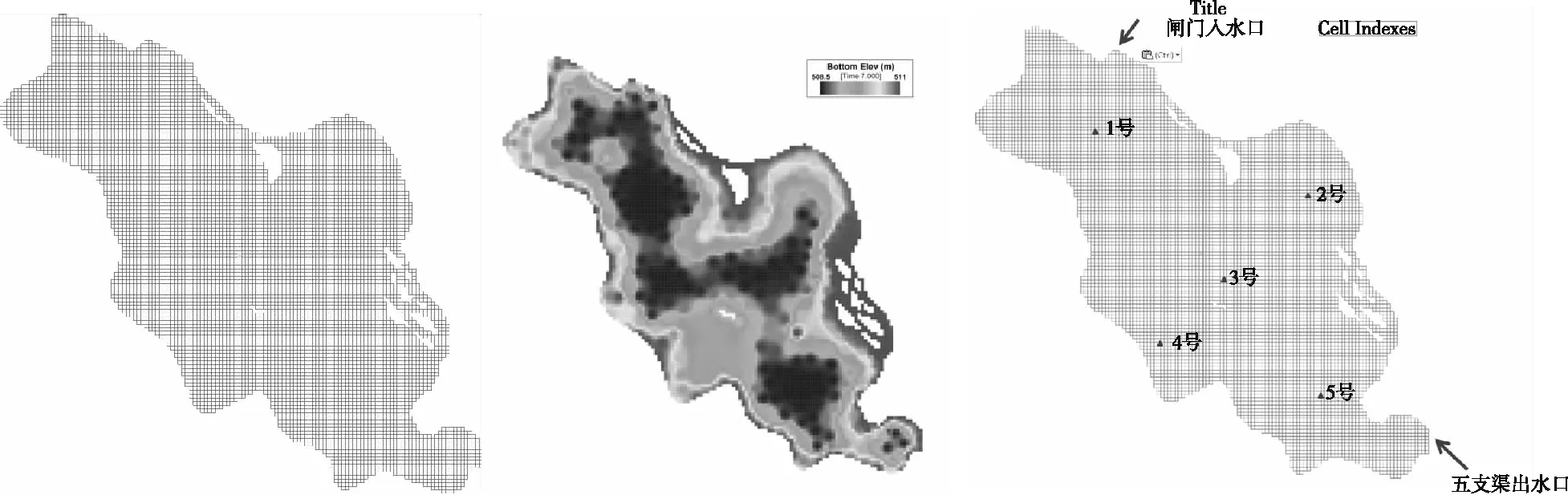
圖2 網格劃分及地形處理 圖3 出入口設置及計算控制點

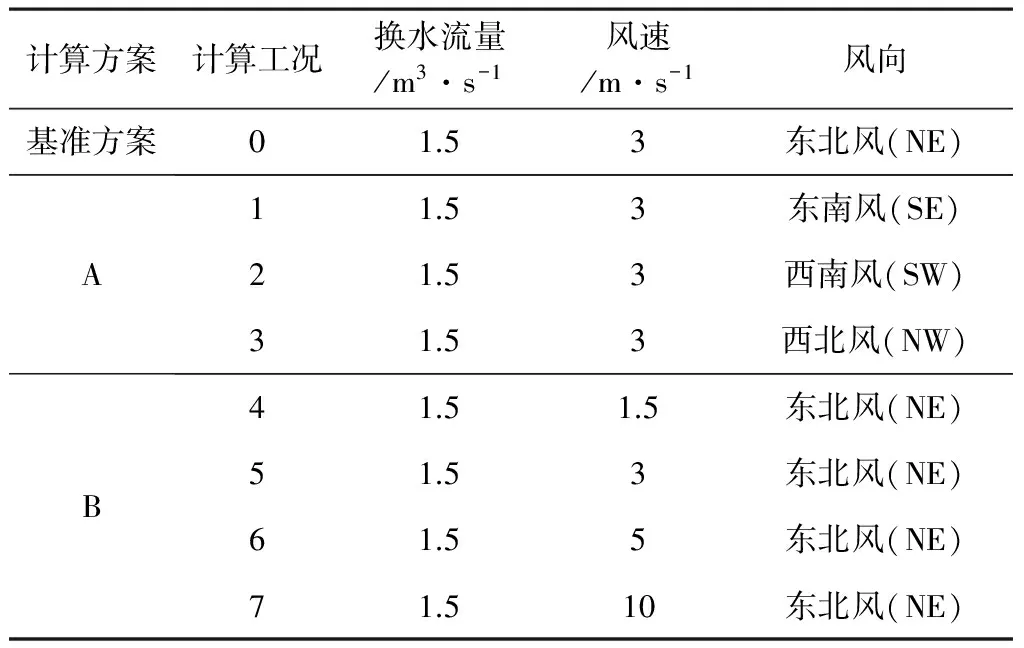
表1 計算方案

其中，基準方案中，風速設定為淺水湖泊風生流最小啟動風速3 m/s，風向為多年主導風向NE，換水流量為1.5 m3/s(南五支渠出湖流量也為1.5 m3/s)。A方案包含3個計算工況，主要研究風向改變對青龍湖1號湖換水方案的影響；B方案主要比較不同風速對青龍湖1號湖的水動力條件和水齡分布影響。在湖區范圍內設置5個監測點，分別分析入湖口、東北沿岸區、湖心區、西南沿岸區和出湖口的水動力和水齡變化，點位設置如圖3所示。

3 計算結果及分析

3.1 風向對青龍湖1號湖水動力條件的影響

風應力是淺水湖泊形成環流的主要驅動力，風向是決定青龍湖1號湖的環流形態的決定性因素。從圖4可知，工況0和工況2的環流形態類似，工況1和工況3的環流形態類似，但是環流的方向相反。在東北和西南風的作用下，東北部湖灣處分別形成兩處小型環流，使得湖灣的水體與湖心區進行交換；工況1和工況3中，在湖心區形成西北-東南方向的大型環流，使得整個湖區的水體得到循環。

同時，不同風向對湖泊不同區域的流速影響不同。以2號點位為例，在東北風的情況下，其流速最大，為0.016 9 m/s，表明在該風向下，東北湖灣區的水動力條件最好，有利于該區域水體的復氧作用，其水質惡化的風險較小；對于4號點位，其水動力條件最好的為工況1和3運行工況，其流速分別為0.016 95 m/s和0.017 04 m/s，而其余兩個工況條件下，流速分別為0.007 44 m/s和0.010 70 m/s，水動力條件較差。由此可見，對于2號、5號，東北風條件下水動力條件最佳，對于3號和4號，分別是西北風和東南風條件下水動力條件最佳。由此，在對湖泊進行生態工程和水質保障工程設計時，應重點對非主導風向條件下水動力條件較差的區域(如3號、4號區域)進行針對性設計，以減少該區域水質惡化的風險(見表2)。

3.2 風向對青龍湖1號湖水齡的影響

對湖泊水動力條件的分析是針對湖泊本身在風場條件下的流場響應進行論證，而針對通過換水改善湖體水質的青龍湖1號湖，通過對水齡的分析能更好地論證換水工程對整個湖泊的水質改善效應。

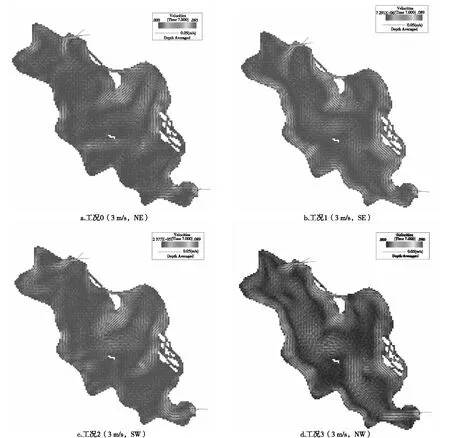
圖4 不同風向條件下青龍湖1號湖流場分布

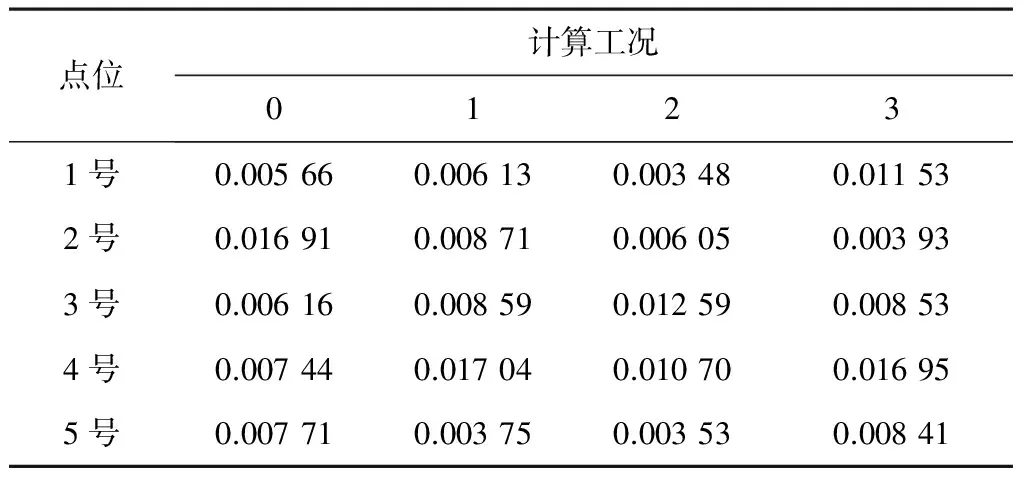
表2 不同風向條件下青龍湖1號湖各點位流速 m/s

圖5描述了不同風場條件下青龍湖1號湖的水齡分布情況。整體來看，1號點位的水齡是5個點位中最小的，且受到風向的影響也最小，這表明入口處附近的首先得到交換，在入湖水質得到保證的前提下，該區域的水質改善效果最明顯。其余湖區的水齡根據風向的不同，其水齡大小有所區別。2號點位在工況0條件下，水齡為5.235 4 d，小于其他3個工況；3號點位的水齡在工況3運行下最小，為4.697 7 d；4號點位最小水齡出現在工況1運行下；5號點位在工況1和工況3運行下的水齡大小相近，均為5.40 d左右。結合水齡平面分布(見圖5)可得出結論：不同風向對青龍湖1號湖區的水齡的改善條件不同，西南風有利于湖泊出入口的水體交換，東南風有利于東南沿岸區的水體交換，西北風有利于湖心區的水體交換。不同風向條件下青龍湖1號湖各點位水齡見表3。

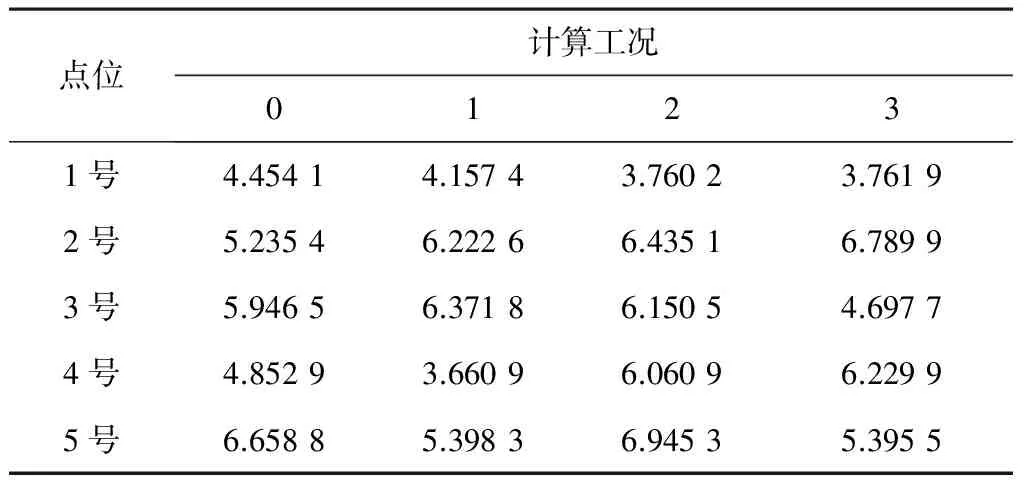
表3 不同風向條件下青龍湖1號湖各點位水齡 d

3.3 風速對青龍湖1號湖水動力特征的影響

風速對淺水湖泊風生流速具有決定性因素。圖6表示了成都市主導風向(東北風)條件下各風速梯度的青龍湖1號湖流場分布。其中1 m/s為成都市常年主導風速，此時各點位中只有5號的流速達到0.006 77 m/s，但該點接近出湖口，速度主要受到出湖流量影響。在此風速下，青龍湖1號湖的其他區域流速基本在0.005 m/s左右，水動力條件極差，整個湖面基本處于“死水”狀態。隨著風速的增加，湖泊的流速明顯加強，水動力條件得到好轉。在5 m/s的風速條件下，整個湖泊的平均流速能達到0.012 m/s以上，湖泊形成明顯的環流場，尤其是近岸淺水區，流速明顯增加，如2號點的流速增加到0.027 28 m/s，是風速1 m/s條件下的4倍。由此，可以得知風速的增加可以使整個湖區的水動力條件得到明顯改善，每個驗證點的流速都隨著風速的增加而得到明顯的提高(見表4)。

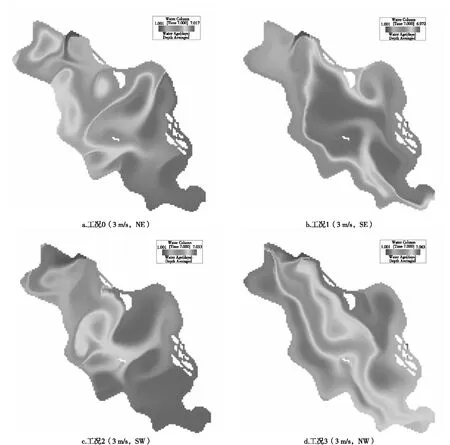
圖5 不同風向條件下青龍湖1號湖水齡分布

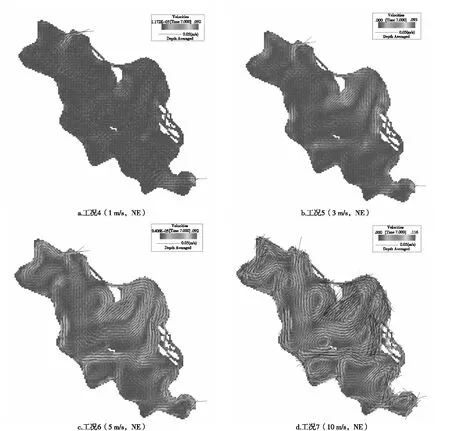
圖6 定常風不同風速條件下青龍湖1號湖流場分布

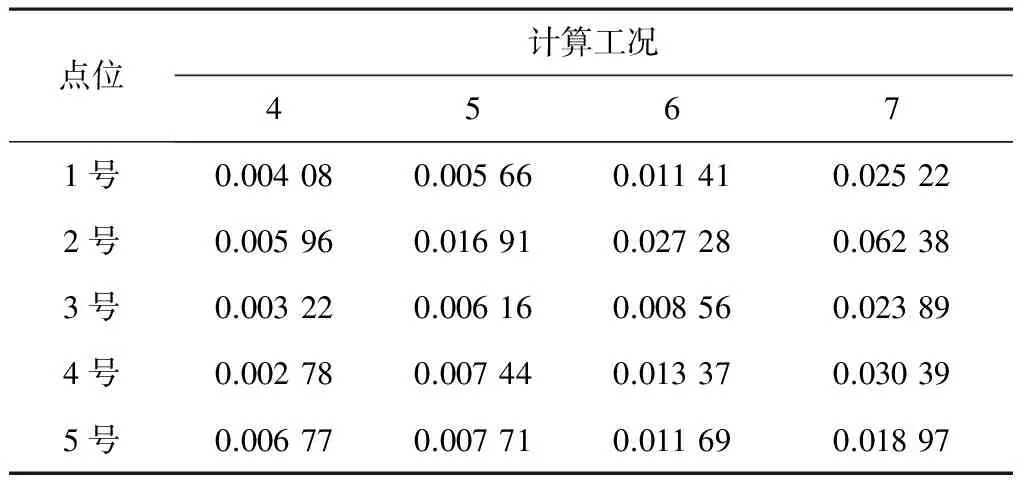
表4 定常風向不同風速條件下青龍湖1號湖各點位流速 m/s

3.4 風速對青龍湖1號湖水齡的影響

在成都市常年主導風向條件下，各個點位的水齡沒有明顯的下降趨勢，對于靠近入湖口的1號點位，在風速從1 m/s增加到3 m/s的情況下，水齡從2.337 3 d增加到4.454 1 d，而當風速增加到5 m/s和10 m/s時，水齡沒有明顯的改變。對于其他點位，水齡也沒有隨著風速和流速的增加而有明顯的減小，反而部分點位的水齡隨著風速的增加而增加，說明過大的風速會阻礙換水效果。由此可以得出結論，在該主導風向條件下，水齡和流速并不呈現完全的負相關的關系，局部形成的湖泊環流會阻止水體的內部交換(見表5、圖7)。

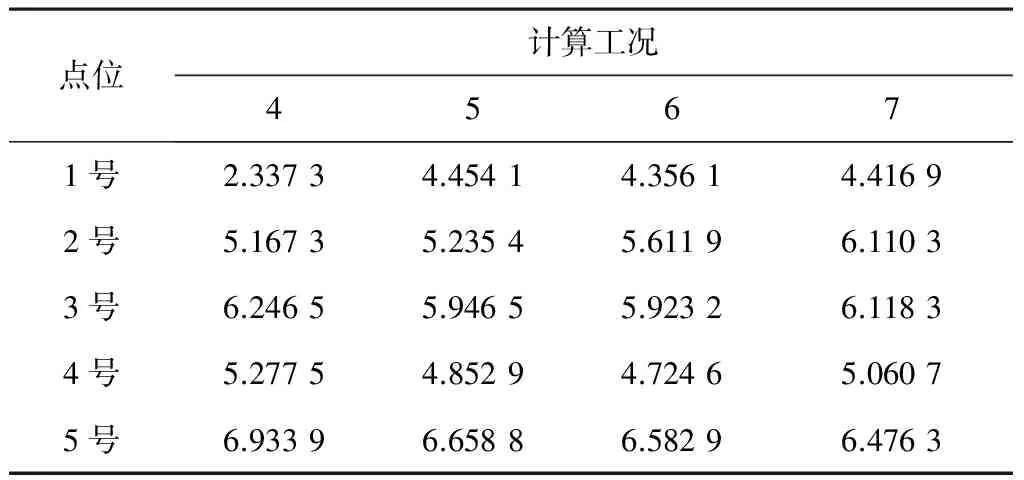
表5 定常風向不同風速條件下青龍湖1號湖各點位水齡 d

4 結論和建議

4.1 結 論

本文利用EFDC模型對成都市青龍湖1號湖進

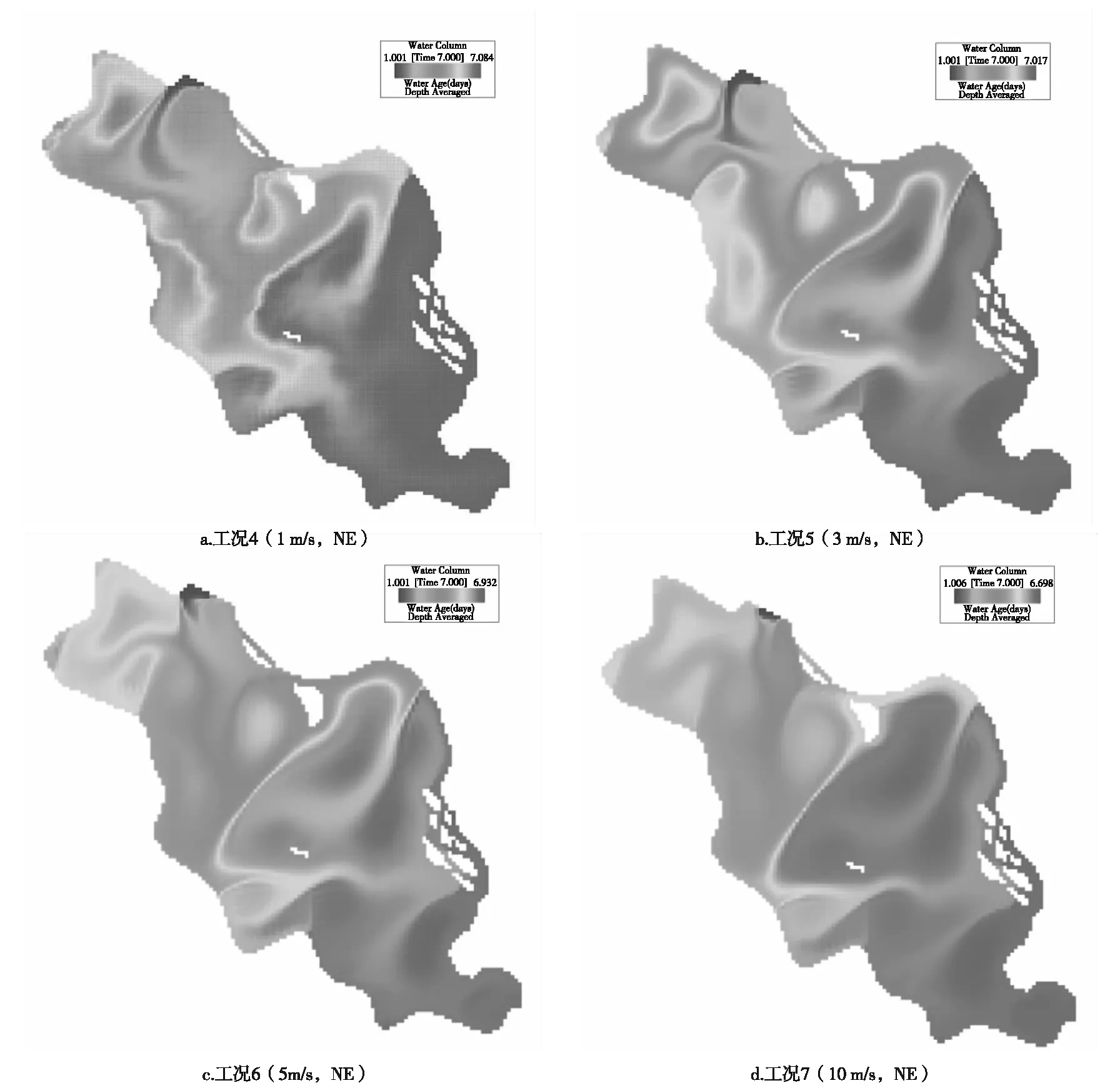
圖7 定常風向不同風速條件下青龍湖1號湖水齡分布

行了三維的流場數學模擬，分析了不同風向、風速條件下，湖泊的流速和水齡分布，并對比分析了不同情景下的湖泊換水方案，得出以下結論：

(1)風向對湖泊的水動力條件具有較大的影響，不同風向形成不同的環流形態特征，東南風和東北風可使整個湖泊形成大型環流，有利于全湖水體循環；而西北風和東南風更易形成局部的小型環流，不利于全湖水體循環。

(2)在西北風的作用下引水對青龍湖1號湖的水動力改善最明顯，而在西南風的作用下引水對1號湖的水動力改善情況則不甚理想。

(3)不同的風向對1號湖水齡的改善情況不同，東北風有利于湖泊東北區域水齡的減小，東南風有利于西南沿岸區域水齡的減小，西北風有利于湖心區水齡減小，西南風有利于湖區西北部水齡的減小。

(4)在成都市主導風向的條件下，風速的增加會使湖泊的水動力條件得到改善，但換水周期并不會隨著風速和流速的增加而減小。

4.2 建 議

城市人工湖泊有利于構建城市景觀和改善城市生態環境。同其他天然淺水湖泊一樣，風力作用是城市景觀淺水湖泊湖流的主要驅動應力。在景觀設計中，為了追求良好的景觀效應而設計的蜿蜒曲折形態會阻礙部分湖區水體交換，造成湖泊水質惡化。在人工水體置換方案的設計和運行中，要充分考慮風生流對其影響，優化設計和運行方案；對于局部水動力條件差的區域，可采取人工強化措施，如水生態系統構建、原位修復、人工曝氣復氧等措施，以避免該區域水質惡化、黑臭，影響整個湖泊的生態和景觀效應。

[1] 郝文彬,唐春燕, 滑磊,等.引江濟太調水工程對太湖水動力的調控效果[J].河海大學學報:自然科學版,2012,40(2):129-133.

[2] 梁云,殷峻暹,祝雪萍,等.MIKE21水動力學模型在洪澤湖水位模擬中的應用[J].水電能源科學,2013(1):135-137.

[3] Hamrick J M, Estuarine environmental impact assessment using a three-dimensional circulation and transport mode[C]//.Estuarine and Coastal Modeling(1991).ASCE,2015.

[4] Ji Z G, Morton M R, Hamrick J M. Modeling Hydrodynamic and Sediment Processes in Morro Bay[C]//Estuarine and Coastal Modeling (1999). ASCE, 2010:1035-1054.

[5] Smagorinsky J. General Circulation Experiments With The Primitive Equations[J]. Monthly Weather Review, 1963, 91(3):99-164.

[6] Zhang W G, Wilkin J L, Schofield O M E. Simulation of Water Age and Residence Time in New York Bight[J]. Journal of Physical Oceanography, 2010, 40(5):965-982.

[7] Li Y, Acharya K, Yu Z. Modeling impacts of Yangtze River water transfer on water ages in Lake Taihu, China[J]. Ecological Engineering, 2011, 37(2):325-334.

2017-01-12

申超(1986-)，男，四川遂寧人，博士，工程師，從事水環境規劃與設計工作。

X321

：B

：1003-9805(2017)03-0023-06