小學數學教材中的數學史——數學家劉徽

江獻

【摘要】劉徽的數學成就在中國乃至世界數學史上都產生了深遠影響，人教版小學數學教材分別介紹了劉徽在小數、面積計算、圓周率計算以及正負數表示方面的成就，文章對以上內容作了詳細介紹，同時還介紹了劉徽的其他數學成就，為小學數學教師進一步了解劉徽的數學成就提供幫助.

【關鍵詞】劉徽；小數；割圓術；負數；陽馬術

劉徽是我國數學史上一位偉大的數學家，他在數學方面取得的成就在中國乃至世界數學史上都產生了深遠影響.他一生取得了許多數學成就，尤其是他在幾何、分數、重差術等方面的研究對數學發展具有深刻的意義.基于劉徽對數學發展所做的重大貢獻，人教版小學數學教材分別在四年級下冊第33頁“小數的意義和性質”部分介紹了劉徽對小數發展的貢獻（圖1）；在五年級上冊“梯形的面積”部分介紹了劉徽的“出入相補”原理（圖2）；在六年級上冊“圓的面積”部分介紹了劉徽的“割圓術”（圖3）；在六年級下冊“負數”部分介紹了劉徽對負數發展的貢獻（圖4）.其內容之多僅次于《九章算術》，因此，為了讓小學一線數學教師能夠更詳細地了解劉徽的數學成就，并將其在教學中進行滲透，以下將結合小學數學教材進一步詳細介紹劉徽的數學成就.

一、徽 數

“徽數”也就是我們今天的小數.公元3世紀左右，劉徽在注解《九章算術》時，我國的長度單位是：丈、尺、寸、分、厘、毫、秒、忽，忽是最小的單位，劉徽在研究中遇到忽以下的數，他沒有繼續命名，而是創造了十進小數，劉徽稱作“徽數”，他在《九章算術注》的方田章圓田術注、少廣章開方術注和少廣章開立圓術注中分別用到了十進小數.這是世界上對小數的最早認識.[1]

二、出入相補原理

出入相補原理是指：一個平面圖形從一處移置它處，面積不變.即若把圖形分割成若干塊，那么各部分面積的和等于原來圖形的面積，因而，圖形移置前后各面積間的和、差有簡單的相等關系.立體的情形也是這樣.劉徽在《海島算經》的“測望術”中使用這一原理，歷史上這一原理至遲在戰國時代就已經被廣泛認識和應用了.[2]今天的小學數學教材利用出入相補原理進行三角形、梯形等平面圖形面積的推導.

三、割圓術

割圓術是劉徽為《九章算術》方田章“圓田術”作注時引入的.《九章算術》提出了圓田術：半周半徑相乘得積步.這就是圓面積公式：

其中S，L，r分別是圓面積、周長和半徑.在劉徽之前人們用圓內接正六邊形的周長代替圓周長.為了證明這一公式，劉徽提出了割圓術，劉徽從圓的內接正六邊形出發，將邊數逐次加倍（圖5），并計算逐次得到的正多邊形的周長和面積.劉徽指出：“以六觚之一面乘半徑，因而，三之，得十二觚之冪.若又割之，次以十二觚之一面乘半徑，因而，六之，則得二十四觚之冪.割之彌細，所失彌少.割之又割，以至于不可割，則與圓合體而無所失矣.”也就是說，當分割的次數無限增加時，則存在圓內接正多邊形面積的極限，此極限就是圓面積，即

劉徽計算到了圓內接正192邊形，求得圓周率的近似值3.14.他自己也認為“此率尚微少”.[3]南北朝時期的祖沖之算出了圓周率數值的上下限：

3.141 592 6<π<3.141 592 7

一般認為這個“正數”范圍的獲得是沿用了劉徽的割圓術.事實上，如果按劉徽割圓術從正六邊形出發連續算到正24576邊形，恰好可以得到祖沖之的結果.[4]

四、負 數

負數一般定義為小于零的數.中國古代沒有負數一詞，但有“負”（亦作負算）.目前國內外一致公認最早的負數記法出現于中國的《九章算術》.《九章算術》“正負術”中給出正確的負數運算法則，公元263年（魏景元四年）劉徽的《九章算術注》把正與負看成是相對存在的數的兩種情況，劉徽指出“正算赤，負算黑.否則以邪正為異”.說明負數可以用黑色算籌或者以斜畫的籌表示，劉徽在世界數學史上第一個采取了把數的正負與加減運算關系統一起來的做法.[3，5]

五、其他成就

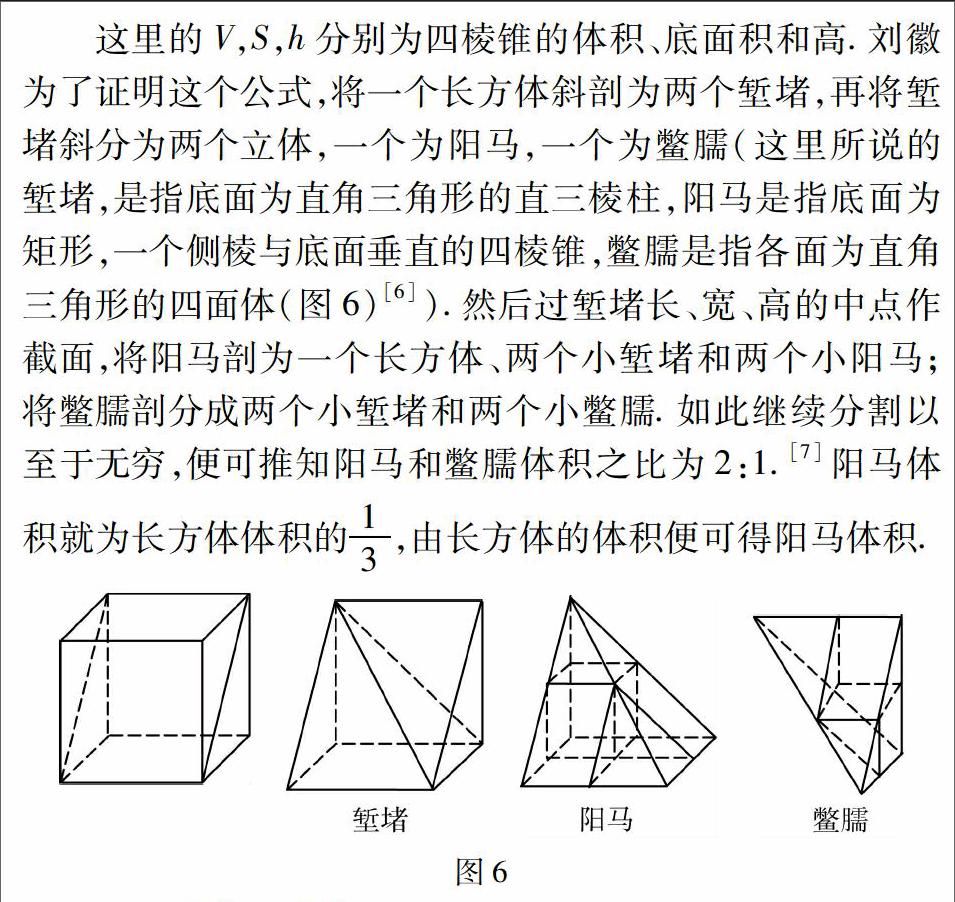
（一）陽馬術

《九章算術》“商功章”陽馬術給出陽馬的體積公式為其三條直角邊乘積的三分之一，即

（二）球體積計算

劉徽作球的外切立方體，再在立方體內作兩個與球半徑相同的互相垂直的圓柱，劉徽稱這兩個圓柱的公共部分為“牟合方蓋”（圖7）.他指出用水平面去截球和“牟合方蓋”所得的面積比為π∶4，因此，球和“牟合方蓋”的體積比也為π∶4，只要能夠求出“牟合方蓋”的體積即可得到球的體積.[8]然而，劉徽沒有能夠直接求出“牟合方蓋”的體積.

并將劉徽的思想上升為理論，提出了祖暅原理“緣冪勢既同，則積不容異”，[9]即兩個等高立體如果在所有等高處的水平截面積相同，則兩個立體的體積相同.

（三）重差術

劉徽在《海島算經》中借助于相似勾股形的比例關系和中國古代的“重差術”計算山上的松高，這是劉徽對中國古代重差理論的進一步發展，展示了勾股比例和重差測量的演化歷程.[3]

【參考文獻】

[1]李迪.中國數學史簡編[M].沈陽：遼寧人民出版社，1984：90.

[2]董杰.出入相補原理在清初正五邊形、十邊形研究中的應用[J].內蒙古師范大學學報（自然科學漢文版），2009（5）：539.

[3]朱家生.數學史（第二版）[M].北京：高等教育出版社，2011（5）：59，60，64.

[4]李文林.數學史概論（第三版）[M].北京：高等教育出版社，2011（3）：86.

[5]王青建.古代的負數記法[J].遼寧師范大學學報（自然科學版），1998（3）：177-181.

[6]蔡偉，李勁.阿基米德和劉徽求積的“余部分割法” [J].天水師范學院學報，2005（4）：1.

[7]徐品方.數學簡明史[M].北京：學苑出版社，1992：50-51.

[8]智廣元.劉徽數學思想探析[J].泰山學院學報，2006（5）：22.

[9]李宇袆.“牟合方蓋”研究[J].雁北師范學院學報，2003（10）：107.endprint