基于學生學情的課例研究與思考

祝劍

[摘 要] 學生是學習的主體，我們的課堂教學必須以學生的學情為基礎，科學地預設問題，這樣才能有效激活學生的問題意識，促進學生數學核心素養的有效發展，繼而保證教學實效.

[關鍵詞] 學情；問題意識；初中數學

數學知識的學習過程是不斷發現問題并解決問題的過程，我們教師切勿憑經驗進行知識灌輸，而應該結合學生的具體學情，通過問題的預設，逐步引導學生逐層地揭開罩在知識表層的一道道面紗.

立足學情的必要性分析

在任何學科的學習中，學生都不應該是被馴服的“小綿羊”，而應該是具備學習主觀能動性的學習者. 教師的“傳道、授業、解惑”對于學生的學習來說是推進、幫助學生學習的外因，學生只有最大限度地發揮其學習的主觀能動性，才能取得最大化的學習成效. 由此可見，學習者才是問題意識的主體，教師應該清楚地認識到產生問題、發現問題并提出問題的都應該是學生這一學習主體. 這就說明，真正的思維來源于自己的發現與認知，解決問題的思路與辦法來自自身對問題的探索. 著名教育家弗雷斯和施瓦茨曾經借助積極信息加工理論對學生自我提問的質量與數量進行過仔細地調查與研究，并得出了“學生自我提問對學生學習的幫助與促進比教師的提問更加具備突破性”的結論，而且，學生突破認知提出的高水平問題能夠促進學生對知識的理解，能使問題的解決更加深入. 因此，發揮學生的學習主觀能動性是培養學生問題意識時首先應該做到的. 對于初中生來說，數學自主學習的方法與能力水平相對來說還比較低下，學生的問題意識還需教師激發、引導與培養，因此，數學教師在教學過程中必須立足于學生的學情，注重問題的設置與引導，讓學生在不同的問題觸動中產生思維沖突，繼而發現并提出新的問題，使學生自身學習的主動性與積極性在問題的發現與探索中得到最大限度的展現與發揮.

課例研究：“相似三角形的判定（2）”

1. 設置問題，幫助學生回顧已學知識

基于學生學情的課堂教學在開課階段應該設置問題，以幫助學生實現從原有認知到新知識的有效鏈接.

預設問題1：我們前面已經學習了哪幾種判定三角形相似的方法？

預設問題2：我們前面學習過判定全等三角形的方法“ASA”，那么類比該方法，你能想出判定三角形相似的新方法嗎？

設計意圖 學生在新知識的學習前已經掌握了一些知識和方法，問題1則是幫助學生完成已學知識的回顧，問題2則是引導學生進一步進行猜想和方法的遷移. 學生通過類比能夠得到猜想：“如果兩個三角形有兩個角對應相等，那么它們相似. ”隨著這一猜想的落地，新的問題隨之而來，而這恰是學生問題意識被激發的體現.

生成性問題1：“兩角分別相等的兩個三角形相似”用數學符號語言如何表示？

生成性問題2：如何證明上述猜想？

在學生思考并解決了上述問題后，新的方法也就在猜想與驗證的過程中得到了.

2. 精選例題并及時鞏固

精選例題的目的在于讓學生能夠及時進行新學知識的應用與鞏固.

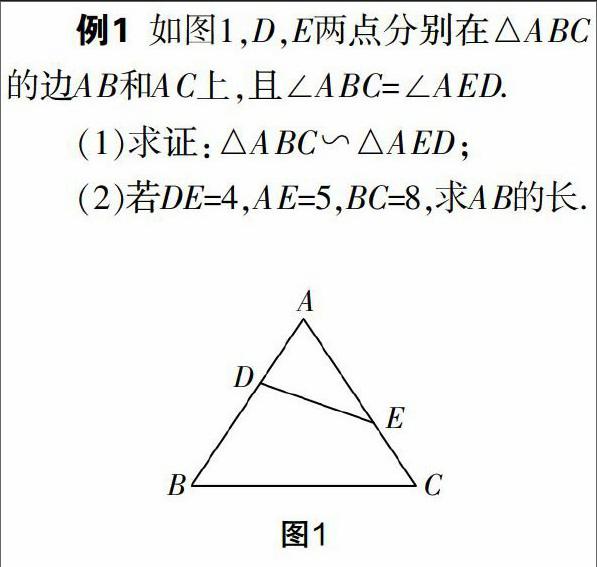
例1 如圖1，D，E兩點分別在△ABC的邊AB和AC上，且∠ABC=∠AED.

（1）求證：△ABC∽△AED；

（2）若DE=4，AE=5，BC=8，求AB的長.

設計意圖 例1的主要目的在于讓學生練習剛學到的新的判定方法，當然，結合學生的實際，在學生完成例1后，還可以適當地進行延展，給學生提供一個變式訓練，如提供“黃金三角形”這一經典圖形讓學生進行同步訓練.

例2 如圖2，在△ABC中，∠ACB=90°，CD⊥AB于點D.

（1）求證：CD2=AD·BD；

（2）想一想：你還能得到哪些與上式相似的乘積式？

設計意圖 學生在前面的學習和問題的解決中已經具備了一定的知識基礎，例2則將學生的問題意識聚焦到“射影定理”基本圖形，這類圖形在后續還有進一步的變式與應用，能為后續學習打下堅實的基礎.

3. 情境拓展，綜合應用規律

從中考數學的要求與難度來看，我們不能僅僅滿足于規律的學習和簡單應用，還應將其置于更為綜合的問題情境中. 為此，筆者在教學過程中引入圓的背景習題，讓學生進行綜合應用.

例3 如圖3，已知△ABC和△ABD都是圓O的內接三角形，點E是AC和BD的交點.

（1）求證：△ADE∽△BCE；

（2）求證：AE·CE=BE·DE.

例4 如圖4，圓O的半徑為5，圓外有一點P，PB與圓交于A，B兩點，PC與圓交于C，D兩點.

（1）求證：PA·PB=PD·PC；

設計意圖 例3和例4以“圓”為背景設置數學問題，因為圓在初中階段是學生比較怕的一個圖形，所以在知識教學的過程中要有意識地進行滲透和訓練. 從教學實踐來看，學生在圓的背景問題中能夠應用新學到的知識和方法進行兩個三角形相似的判定，這個過程不僅是綜合應用知識解決問題的過程，也有助于學生增強數學學習的信心——解決以圓為背景的綜合題.

4. 基于學情，師生小結

每節課最后都應該讓學生清楚地知道學到了什么，因此，在課堂結束之前教師應該引導學生進行必要的小結，而小結也應該基于學生的具體學情并通過預設問題引導學生完成. 例如本節課，筆者結合所教班級學生的實際情況，借助如下幾個問題來引導學生完成小結.

問題1：小明說：“要想判斷兩個直角三角形是否相似，只要找到兩者有一組角對應相等就可以了. ”通過這一節課的學習，請你判斷一下小明的說法是否正確.

問題2：通過這節課的學習，你覺得哪一種圖形是我們在解決數學問題的過程中值得積累的？（說出其在具體的數學問題解決中有哪些便利）

問題3：有同學發現“過圓上任意一點作直徑的垂線段，則垂足將直徑分成的兩條線段的積等于該垂線段的平方”，結合本節課所學的知識和方法，判斷此發現是否正確.

幾點反思

結合新課程教學理念和本節課的教學實踐，筆者有如下幾點思考.

1. 把握學情和理解課標同等重要

學生是學習的主體，課標則是我們實施課堂教學的重要準繩，我們在備課和進行問題設計時，兩者都得兼顧，要考慮到我們考綱的具體要求和學生的實際，只有這樣，才能讓學生做到知其然，且知其所以然. 如果所教班級學生的基礎較好，應該為了學生數學素養的有效提升甚至可以“上不封頂”，實現從“教教材”到“用教材教”的跨越性發展.

例如，上面的例3和例4，就是基于學生的學情進行的例題設計——以圓為背景研究相似三角形，在解決問題的過程中，學生不僅用到了新的知識，還結合圓周角性質有了新的發現——“相交弦性質”，繼而促進學生對初中幾何有一個較為整體的認識.

2. 預設問題，促進學生多維度對話與互動

學習是一個循序漸進的過程，這個過程從何處開始？如何幫助學生沿著正確的方向前行？筆者認為，需要我們教師結合學生實際進行問題預設，借此激發學生的問題意識，生成新的問題. 問題意識的觸動、產生以及展現，自然也會遵循這樣的客觀規律. 對于初中生來說，這個過程更加明顯，并且必不可少. 因此，教師在初中數學教學過程中，應冷靜對待學生的不會或不善提問，應盡量挖掘教材內容的內涵以及教材之間的關聯，精心設計并引導學生意識到問題意識的發展. 在學生逐步產生問題意識之后，首先突破自我敢于提問，再引導學生注重提問的訣竅，努力做到“善問”，從心理到能力均有所突破. 當然，每個學生因為自身水平以及語言表達、情感、意志品質等因素，在發現與提出問題中均會有不一樣的表現，因此，教師在設計評價標準、引導方式、訓練方法上要有所區別，要使得每個學生個體在教師的精心設計與教學中均能受益匪淺. 當然，教師在整個教學過程中更需關注學生的參與環節，以及學生參與的方式和表現. 如果學生能夠將活動參與的主要精力放在質疑與探究活動中，那么這個過程必然是學生問題意識形成與強化的過程. 學生這一主體參與的基本形式是很多教育家早就關注并探究的，主體參與表現為以語言、邏輯、概念等內容為媒體的社會性、活動性學習是維果斯基提出的觀點；而將主體參與看成個人活動與社會性活動交互，并注重在探究過程中經驗的再構成，則是杜威的觀點.