利用GeoGebra軟件輔助初中函數教學案例的研究

聶霞

[摘 要] 本文利用GeoGebra軟件引導學生進行一次函數的探究實驗，讓學生通過觀察、猜想、實驗、歸納、推理、交流等數學活動過程，體會和學會探索問題的一般方法.

[關鍵詞] GeoGebra軟件；使用；函數；教學案例

引言

初中數學新課標的出現，大力加強了信息技術在數學教學中的應用，強調以學生動手為主的數學學習方式，目的是提高學生學習數學的積極性，提高學生的數學應用意識，培養學生利用所學的數學知識和計算機技術去認識問題和解決實際問題的能力. 一方面，這一整合有利于學生對數學本質的理解以及數學應用能力的提高；另一方面，也增加了學習時間和學習難度. 所以，要用好新課標，必須采取有別于傳統的數學學習方式. 在新課標的教學中，利用信息技術為數學思想方法注入更多、更廣泛的內容，能使學生擺脫繁重的、乏味的數學演算和數值計算，能促進數學同其他學科之間的結合，從而使學生有時間去做更多的創造性工作，并引導學生對某一數學知識進行探究，從而引入、猜想、歸納、驗證，使學生親歷數學建構過程，逐步掌握認識事物、發現真理的方式和方法，培養創造能力，提高數學素養. 在新課標教學實踐中，筆者利用GeoGebra軟件采用驗證型實驗和設計型實驗進行教學.

GeoGebra軟件使用簡介

GeoGebra軟件是由美國佛羅里達州亞特蘭大大學數學系教授Markus Hohenwarter設計的，它是集代數、幾何與微積分于一體的動態數學教育軟件. GeoGebra 能夠做到幾何圖形與代數方程的同步變化，展示數學對象動態生成的全過程，是一款專門為中學數學教育設計的動態數學軟件，且入門容易，操作簡單方便，有著強大的圖形和圖像功能. 打開GeoGebra軟件窗口，如圖1， 菜單上方為工具欄，有各種繪圖工具和輔助工具，左側有一個“代數區”，用來顯示所輸入的代數表達式，中間有一個“繪圖區”，可使用繪圖工具在繪圖區中利用鼠標作圖，也可在命令欄中輸入命令，在繪圖區繪圖. 右側可顯示“電子表格區”，通過“查看”菜單可顯示出. 每個單元格都對應相應的名稱，不但可以輸入數值，還可以輸入數學對象，在電子表格中輸入的數學對象會在繪圖區中給出相對應的圖像，并以單元格的位置名稱命名. 下側是命令列，可直接輸入代數式及相關函數. GeoGebra軟件能夠同時處理代數與幾何功能，若利用工具欄在繪圖區畫出圖形，則代數區就會出現對應的方程表達式. 反過來，若利用命令列輸入代數方程式，則繪圖區便出現對應圖形，代數區也顯示出相應的表達式. 若代數式參數發生改變，則繪圖區的圖形也會隨之改變，反之亦可. 它把幾何圖形和代數式的關系動態地結合在一起. 對于GeoGebra軟件的詳細使用說明，可以點擊菜單中的 “幫助”，通過聯網查看相關的教程或者進入GeoGebra論壇進行學習.

一次函數的圖像和性質的實驗探究

（一）驗證型實驗的構建

1. 研究問題

非洲大草原上一只矯健的野兔遇到了一只饑餓的豺，野兔的奔跑速度恒為每秒4.5米，豺的奔跑速度恒為每秒5米. 遇到時，二者僅相距5米，假定二者同時起跑.

（1）分別寫出二者距豺起跑點的距離y與出發的時間x的關系式；

（2）結合實際情況，饑餓的豺最多只能堅持跑10秒，則誰能獲勝？

2. 分析問題

顯然，根據正比例函數和一次函數的定義及一般形式，我們可以很輕松地寫出二者距豺起跑點的距離y與出發的時間x的關系式：

y=5x（豺）和y=4.5x+5（野兔）

那么，結合實際情況，饑餓的豺最多只能堅持跑10秒，誰能獲勝呢？要想解決這個問題，我們不妨借助函數圖像來進行研究.

3. 實驗操作步驟與指導

Step1 在GeoGebra軟件的命令窗口中鍵入命令：

>> y=5x

>> y=4.5x+5

于是在代數區中便會顯示出——

直線 f ： y=5x

g ： y=4.5x+5

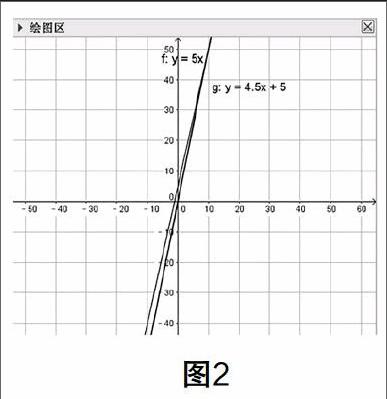
在繪圖區中便會顯示出二者的函數圖像，如圖2.

從圖中可以看出，二者均單調遞增，且從圖中可以明顯地看出二者的函數圖像隨著x的增大而不斷靠攏，最終在x=10（秒）處相交，即豺和野兔之間的距離隨著時間的推移不斷縮小，并在10秒鐘時豺將野兔捕獲！

4. 實驗結論的驗證

由于豺要將野兔捕獲，則二者距豺原始起跑點的距離y（米）必相等，于是有5x=4.5x+5，即0.5x=5，所以x=10（秒），即豺在第10秒時將野兔捕獲.

通過以上實驗操作，學生能觀察出二者的圖像特征，找到二者的變化規律并最終對問題進行驗證.

（二）設計型實驗的構建 1

1. 研究問題

正比例函數y=kx（k≠0）的圖像特征和函數性質.

2. 實驗要求與建議

要求：請同學們自主探索后彼此之間分小組討論研究，填寫實驗報告表中的相關內容.

建議：在同一圖形窗口界面中將定義域區間取為[-10，10]，參數k分為k>0 和k<0進行研究. （實驗時k的值由學生自己決定）

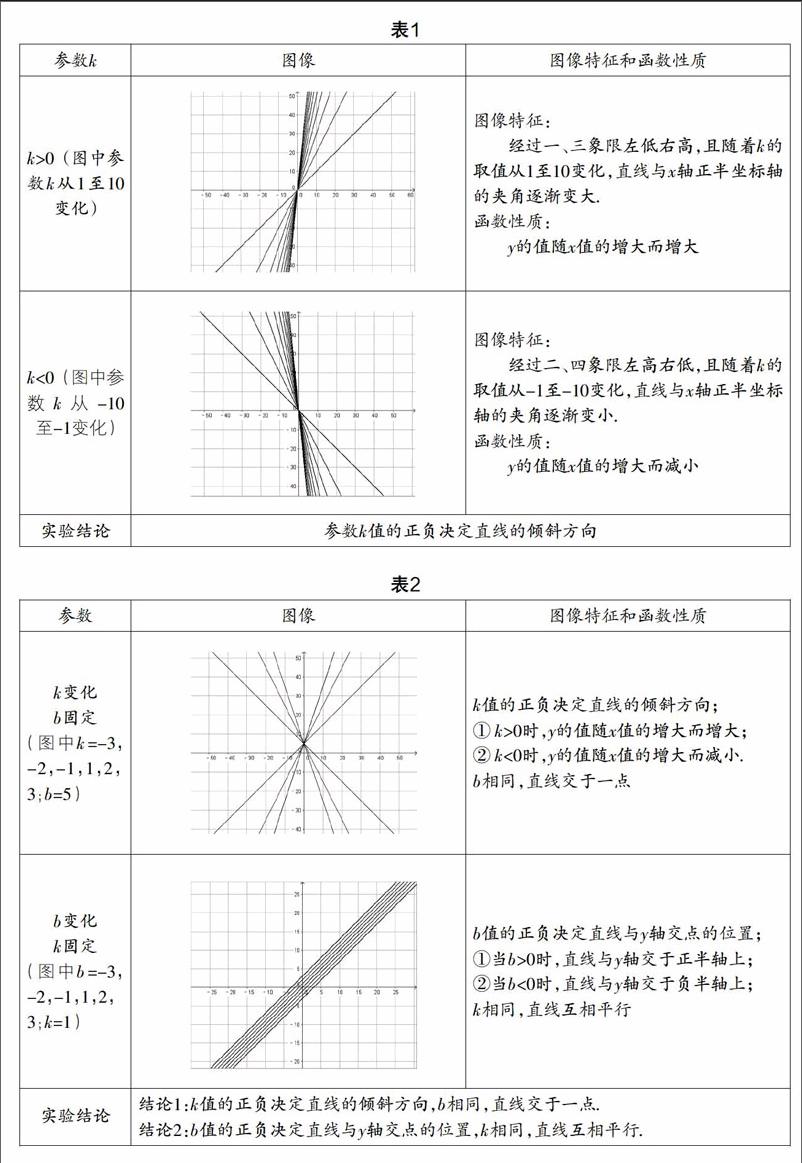
3. 實驗報告表的設計樣例（如表1）

（三）設計型實驗的構建2

1. 研究問題

k，b對一次函數y=kx+b（k≠0，x∈R）的圖像和性質有何影響？

2. 實驗要求與建議

要求：從無序實驗到有序探索，請同學們彼此之間分小組討論研究，并填寫實驗報告表中的相關內容.

建議：將定義域區間取為[-10，10]，k，b兩個參數要一個一個研究，研究一個參數時，另一個參數保持不變.

3. 實驗報告表的樣例參數圖像實驗結論（如表2）

（四）設計型實驗的構建3

1. 研究問題

k，b對一次函數y=kx+b（x∈R）的圖像位置有何影響？

2. 實驗要求與建議

要求：請同學們獨立研究，填寫實驗報告中的相關內容.

建議：將定義域區間取為[-10，10]，根據k，b的符號變化，探究畫圖.

3. 實驗報告表的樣例（如表3）

課外實驗探究設計樣例

1. 研究問題

探究函數y=kx+b與y=kx+b的圖像特征和函數性質

命令提示：在GeoGebra中用abs（x）表示函數x.

2. 實驗報告表的設計樣例（如表4）

結束語

在初中數學新課標教材的基本初等函數的教學過程中，利用GeoGebra軟件讓學生在計算機上進行自主探究實驗，讓學生通過觀察、猜想、實驗、歸納、推理、交流等數學活動過程，體會和學會探索問題的一般方法，不僅可以使學生掌握并應用函數性質解決問題，還可以培養團隊意識和大膽猜想、樂于探究的良好品質，讓學生體驗到成功的喜悅.