帶有p-Laplacian算子的分?jǐn)?shù)階微分方程多點(diǎn)邊值問(wèn)題正解的存在性

張 艷，馬德香

（華北電力大學(xué)數(shù)理學(xué)院 北京 102206）

帶有p-Laplacian算子的分?jǐn)?shù)階微分方程多點(diǎn)邊值問(wèn)題正解的存在性

張 艷，馬德香

（華北電力大學(xué)數(shù)理學(xué)院 北京 102206）

在以下帶有p-Laplacian算子的分?jǐn)?shù)階微分方程多點(diǎn)邊值問(wèn)題中：

其中Dα，Dβ是Riemann-Liouville分?jǐn)?shù)階導(dǎo)數(shù)，f∶［0，+∞）→［0，+∞）是連續(xù)函數(shù)，文章的新奇之處在于運(yùn)用Guo-Krasnoselskii不動(dòng)點(diǎn)定理來(lái)研究了一類含參量的帶有p-Laplacian多點(diǎn)邊值問(wèn)題正解的存在性及不存在性.

分?jǐn)?shù)階微分方程；p-Laplacian算子；多點(diǎn)邊值問(wèn)題；不動(dòng)點(diǎn)定理

0引言

分?jǐn)?shù)階微分方程邊值問(wèn)題近年來(lái)得到了很多學(xué)者的關(guān)注，具體見(jiàn)參考文獻(xiàn)[1-7]，然而直到近幾年帶有p-Laplacian算子的分?jǐn)?shù)階微分方程邊值問(wèn)題的研究才開(kāi)始興起，這是因?yàn)橛善浣⒌哪Ｐ驮诙嗫捉橘|(zhì)中的湍流現(xiàn)象，在流變學(xué)、材料科學(xué)、粘塑性力學(xué)等領(lǐng)域有著廣泛應(yīng)用，研究帶有p-Laplacian算子的分?jǐn)?shù)階微分方程邊值問(wèn)題具有較大的研究前景.近年來(lái)有一些作者開(kāi)始研究帶有p-Laplacian算子的分?jǐn)?shù)階微分方程邊值問(wèn)題，例如在文獻(xiàn)[8]中，作者陳泰永運(yùn)用重合度理論研究了以下帶有p-Laplacian算子的分?jǐn)?shù)階微分方程兩點(diǎn)邊值問(wèn)題：

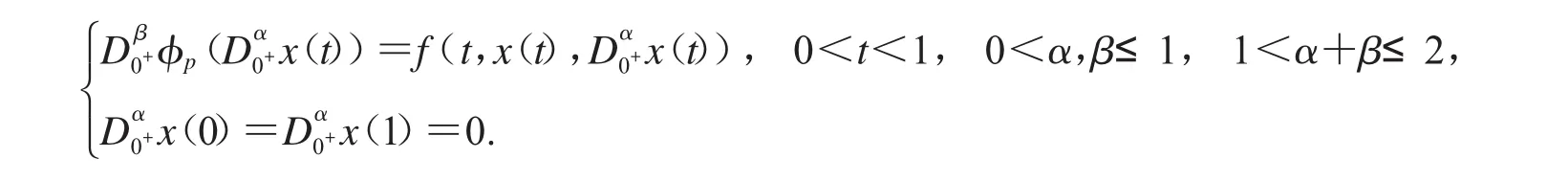
在文獻(xiàn)[9]中，作者韓振來(lái)通過(guò)運(yùn)用Guo-Krasnoselskii不動(dòng)點(diǎn)定理研究了以下帶有p-Laplacian算子的分?jǐn)?shù)階微分方程兩點(diǎn)邊值問(wèn)題：

受以上文獻(xiàn)啟發(fā)，本文將運(yùn)用Guo-Krasnoselskii不動(dòng)點(diǎn)定理來(lái)研究以下邊值問(wèn)題

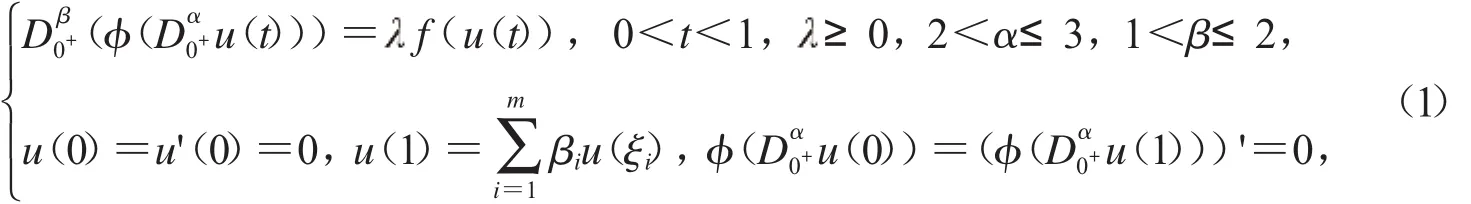
在本文中，假設(shè)以下是成立的：

（H2）f∶［0，+∞）→［0，+∞）是連續(xù)的；

（H3）φ∶R→R為非減奇函數(shù)，且存在非減同胚映射Ψ1，Ψ2，滿足

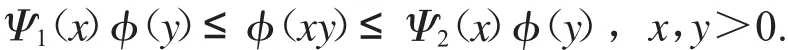
1 預(yù)備知識(shí)和引理

1.1 預(yù)備知識(shí)

1.1.1 α＞0，定義函數(shù)y∶（0，∞）→R的α階Riemann-Liouville分?jǐn)?shù)階積分為

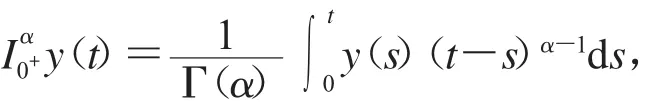
其中Γ（·）是歐拉積分，等式右端在（0，∞）上逐點(diǎn)定義.

1.1.2 α＞0，定義函數(shù)y∶（0，∞）→R的α階Riemann-Liouville分?jǐn)?shù)階導(dǎo)數(shù)為

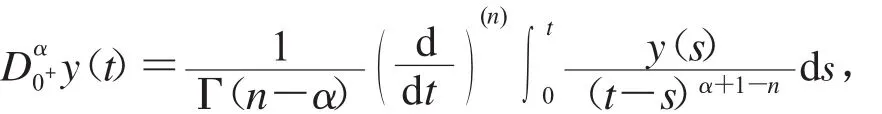
其中n＝[α]+1，等式右端在（0，∞）上逐點(diǎn)定義.

1.2 引理

1.2.1 假設(shè)α＞0，若u∈C（0，1）∩L（0，1）有α階Riemann-Liouville導(dǎo)數(shù)，則

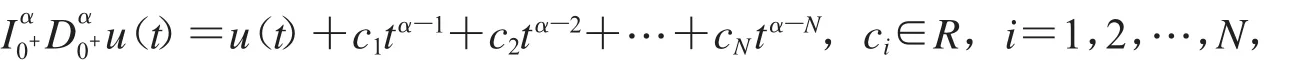
其中N為大于或等于α的最小整數(shù).

1.2.2[10]設(shè)x∈C+[0，1]:＝{x x∈C[0，1]，x（t）≥0，t∈[0，1]}.下列邊值問(wèn)題：

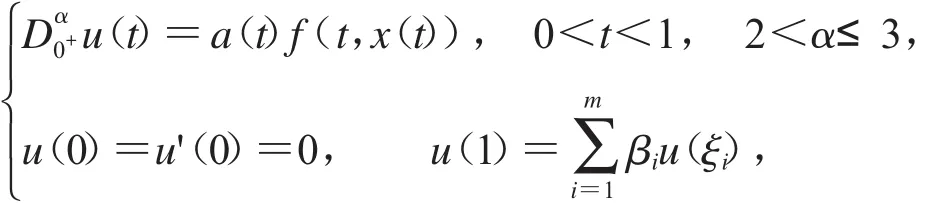
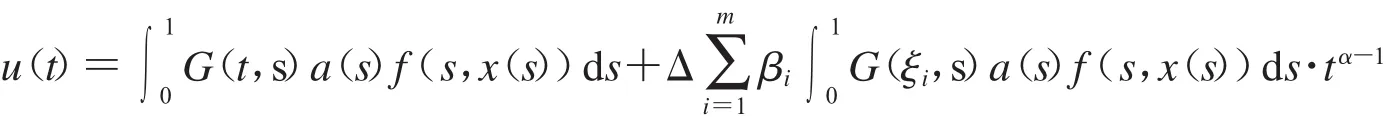
其中

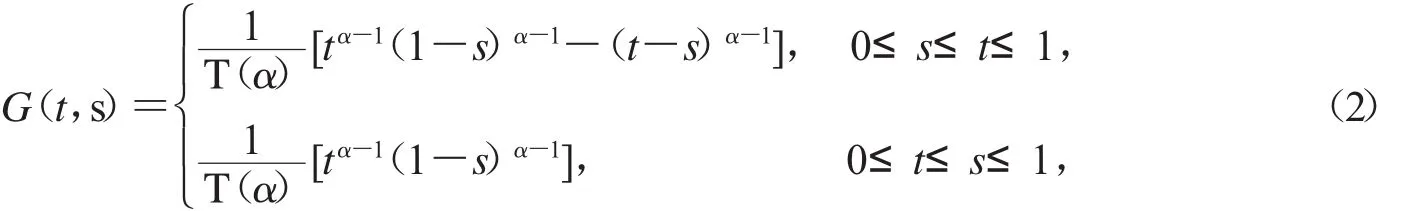
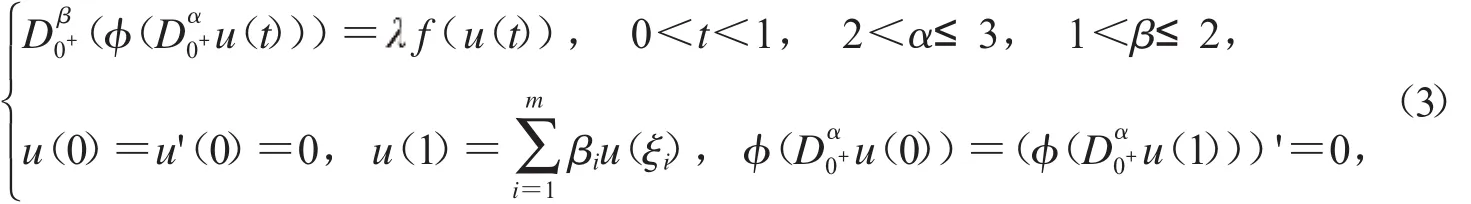
有唯一解

其中G（t，s）見(jiàn)式（2），而證明：

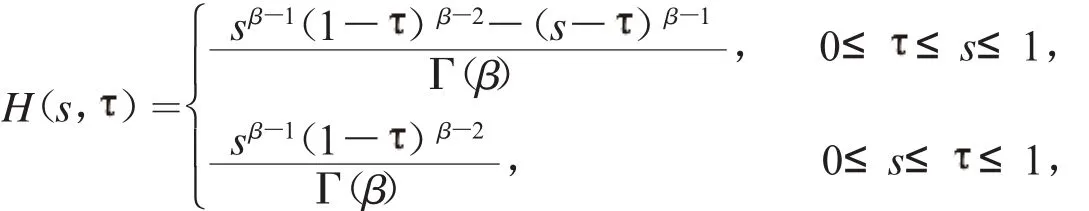
根據(jù)引理1.2.1和1＜β≤2，得

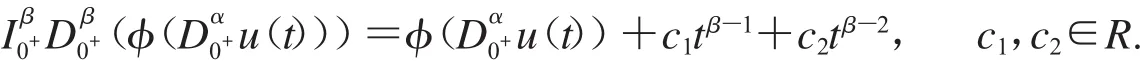
由式（3），有

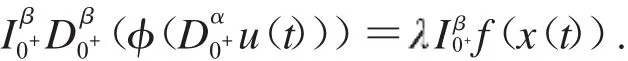
即

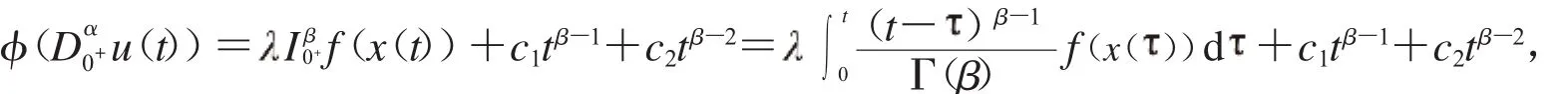
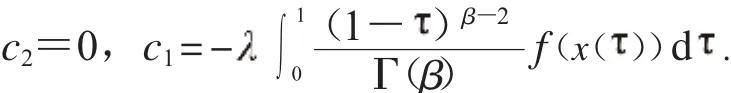
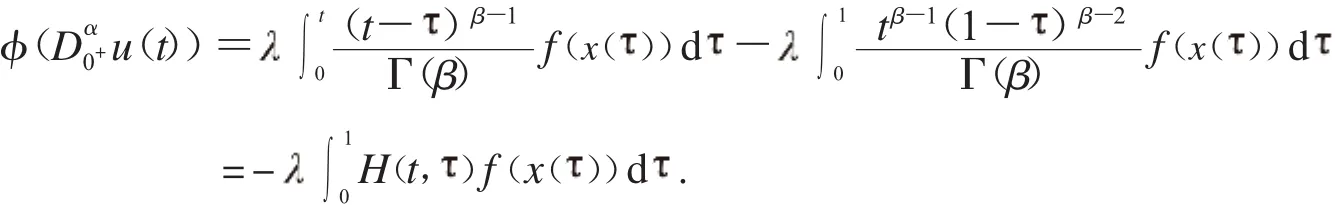
因此：

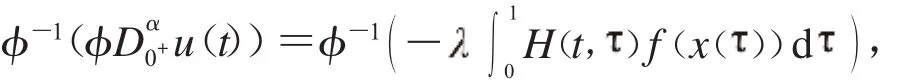
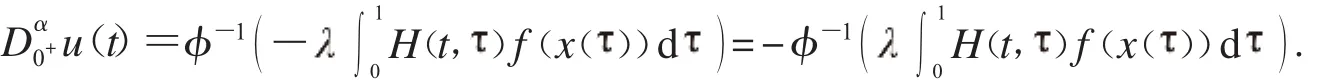
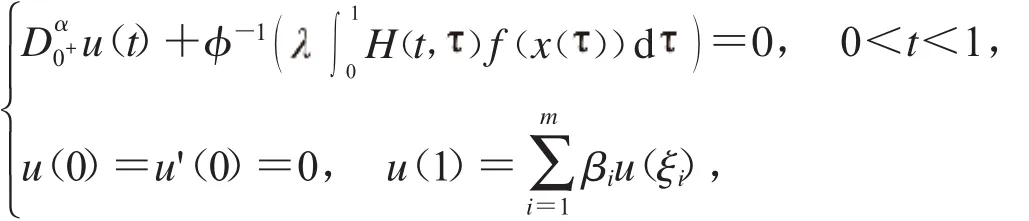
那么根據(jù)引理1.2.2，可知式（3）有唯一解

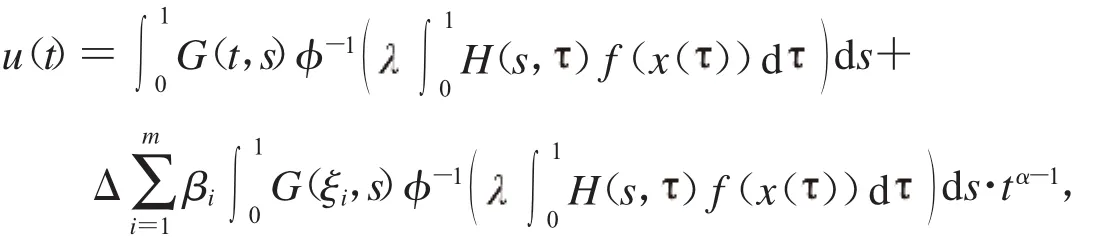
證明完成.

1.2.4[11]G（t，s）有下列性質(zhì)：

（1）對(duì)于任意的（t，s）∈[0，1]×[0，1]，G（t，s）≥0.（2）給定s∈[0，1]，則對(duì)于任意的t∈[0，1]，

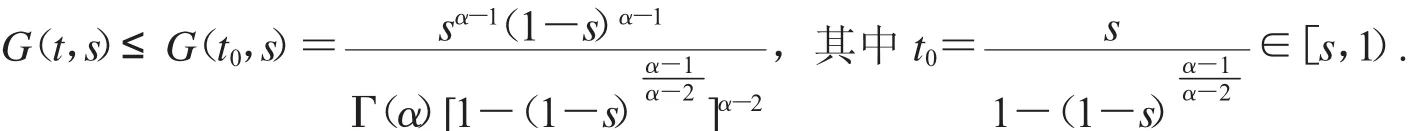
（3）給定s∈[0，1]，則對(duì)于任意的t∈[0，1]，有G（t，s）≥ρ（t）G（t0，s），其中

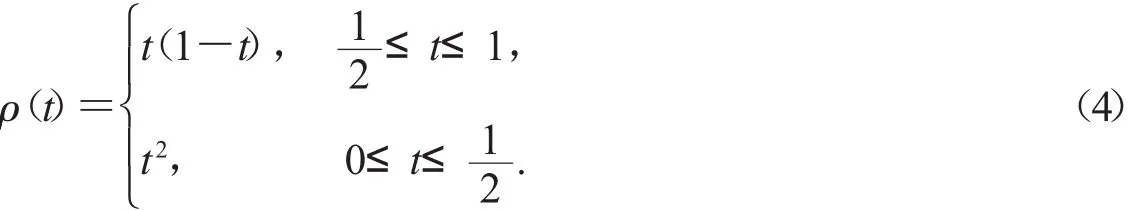
1.2.5[12]H（s，）有以下性質(zhì)：

1.2.7[14]（Guo-Krasnoselskii不動(dòng)點(diǎn)定理） E為Banach空間，P?E是一個(gè)錐，設(shè)Ω1，Ω2是E中的兩個(gè)有界開(kāi)子集，且θ∈Ω1?Ω1?Ω2，有T∶P∩（Ω2Ω1）→P為全連續(xù)算子，且滿足

（1）Tu≤u，u∈P∩?Ω1，Tu≥u，u∈P∩?Ω2，或者

（2）Tu≥u，u∈P∩?Ω1，Tu≤u，u∈P∩?Ω2，

則算子T在P∩（Ω2Ω1）中存在不動(dòng)點(diǎn).

定義算子T∶P→P如下：

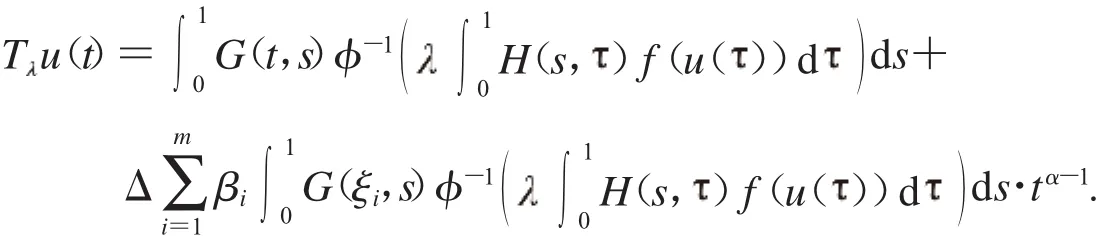
1.2.8 T∶P→P是全連續(xù)算子.

證明：由引理1.2.4，得

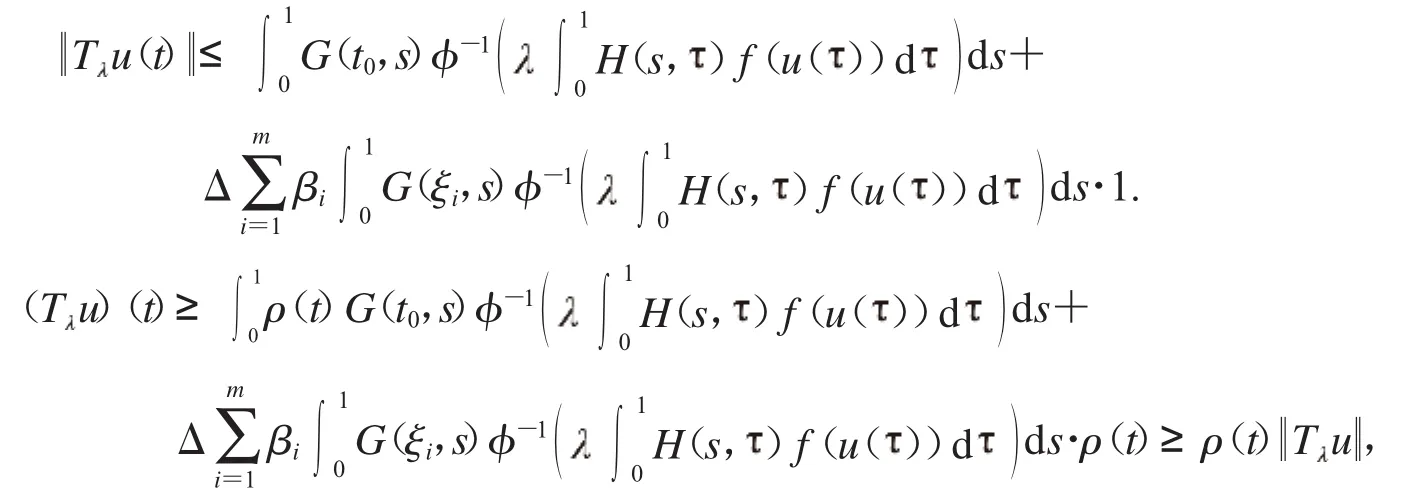
下面證明T的緊性，設(shè)Ω?P是有界的，則存在正常數(shù)M＞0，對(duì)于所有的u∈Ω，有u≤M.令k＝max+1.當(dāng)u∈Ω，t∈[0，1]時(shí)，有

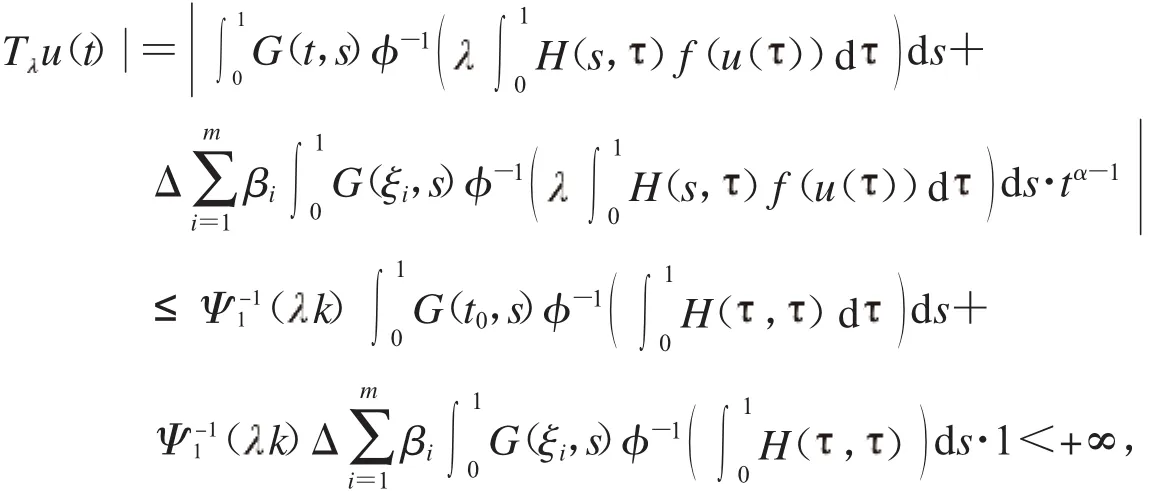
因此，T（Ω）是一致有界的.

另一方面，因?yàn)镚（t，s）在[0，1]×[0，1]上是連續(xù)的，在[0，1]×[0，1]是一致連續(xù)的，因此對(duì)于任意的ε＞0，存在δ＞0，當(dāng)t1，t2∈[0，1]，當(dāng)t1-t2＜δ，有

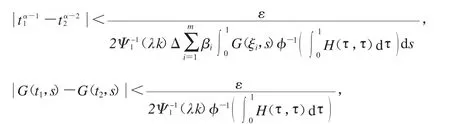
對(duì)于所有的u∈Ω，

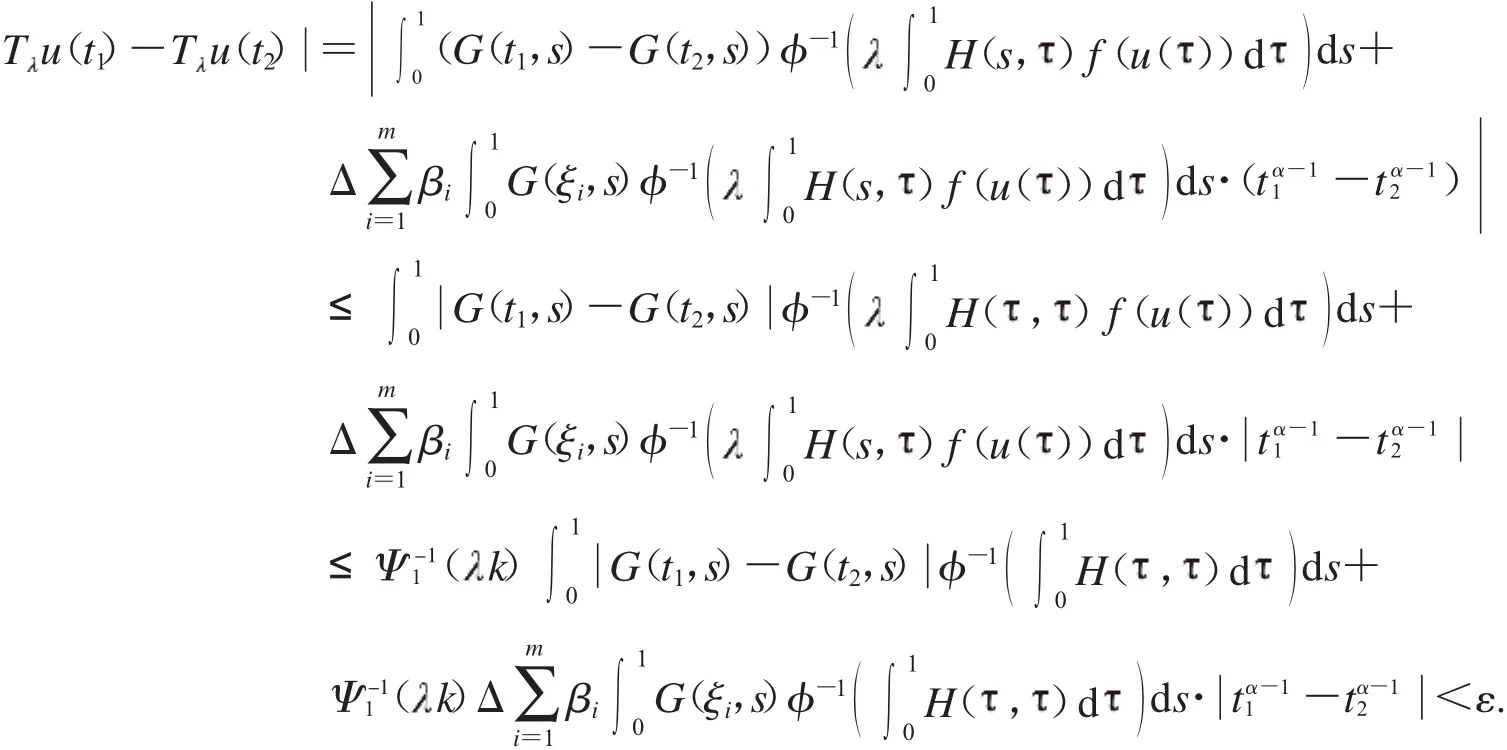
因此T（Ω）是等度連續(xù)的.再由Arzela-Ascoli定理，可知T是緊的，從而得到T∶P→P是全連續(xù)算子.證明完成.

2 正解的存在性與不存在性

為方便起見(jiàn)，引入以下符號(hào)，

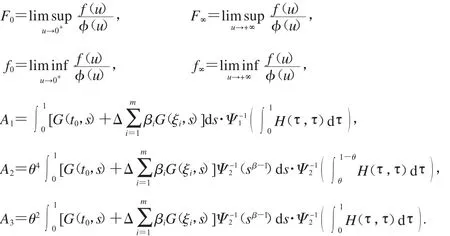
2.1 正解存在性定理的證明

分?jǐn)?shù)階微分方程（1）至少有一個(gè)正解.（當(dāng)f∞＝+∞，F(xiàn)0＝0時(shí)，記f-∞1＝0，F(xiàn)0-1＝+∞.）

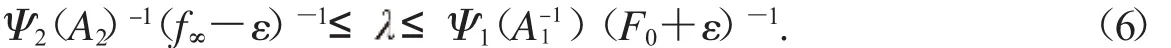
以下證明分為兩部分.

第一步：由F0的定義可知，r1＞0，

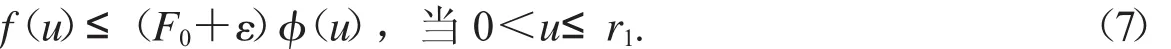
對(duì)于u∈P且u ＝r1，

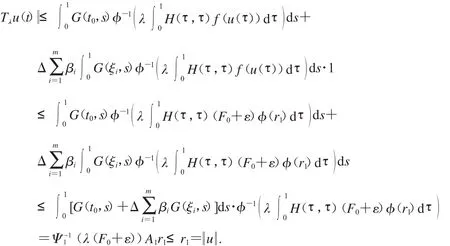
取Ω1＝{u∈E＜r1}，有

第二步：由f∞的定義可知，r3＞0

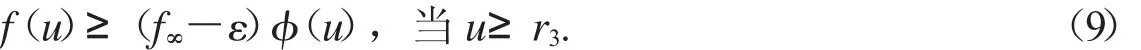
取r2＞ r3，如果u∈P且u ＝r2＝max{2r1，r3}，由式（6）和（9）可得

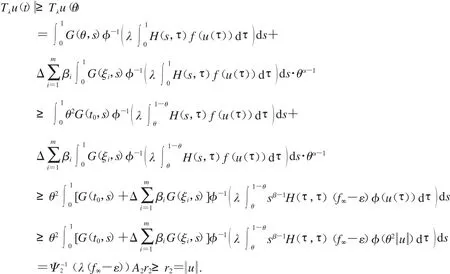
故Ω2＝{u∈E＜r3}取，得

根據(jù)式（8）、（10）以及定理1.2.7可得，T中有一個(gè)不動(dòng)點(diǎn)u∈P∩（Ω2Ω1）且滿足r1≤u ≤r2，顯然u就是分?jǐn)?shù)階微分方程邊值問(wèn)題（1）的正解.證明完成.

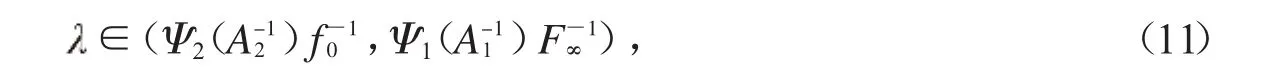
f0Ψ（1A-11）＞F∞Ψ（2A-21）成立.那么對(duì)于則分?jǐn)?shù)階微分方程（1）至少有一個(gè)正解（.當(dāng)f0＝+∞，F(xiàn)∞＝0，有f-01＝0，F(xiàn)-∞1＝+∞.）證明：當(dāng)滿足式（11），可知 ε＞0，滿足

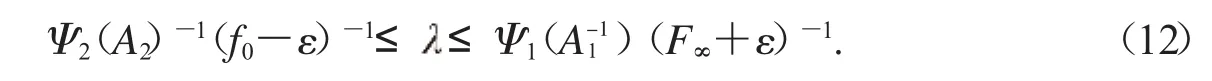
以下證明分為兩部分.

第一步：由f0的定義可知，r1＞0，

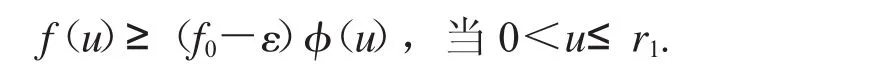
對(duì)于u∈P且u ＝r1，類似于定理2.1.1第二部分的證明方法，可取Ω1＝{u∈Eu ＜r1}，有

第二步：選取R1＞0

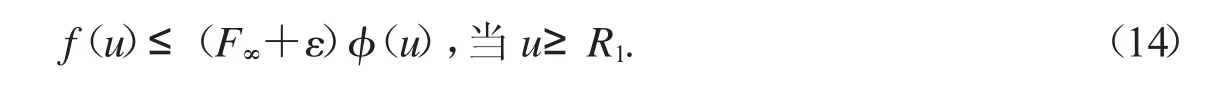
接下來(lái)，考慮兩種情況：

情況一：假設(shè)f是有界的.N＞0，有

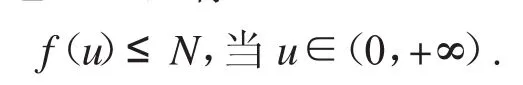
取r3＝max{2r1，φ-（1N）A1}，對(duì)u∈P且u＝r3，有

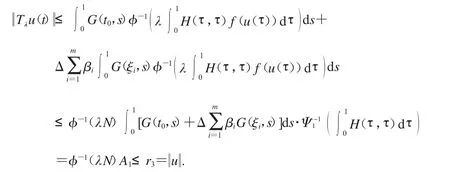
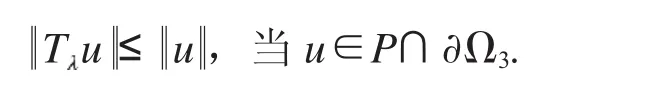
情況二：假設(shè)f是無(wú)界的.則存在r4＞max{2r1，R1}使得

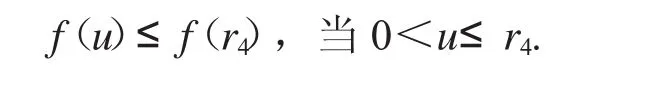
對(duì)于u∈P且u ＝r4，

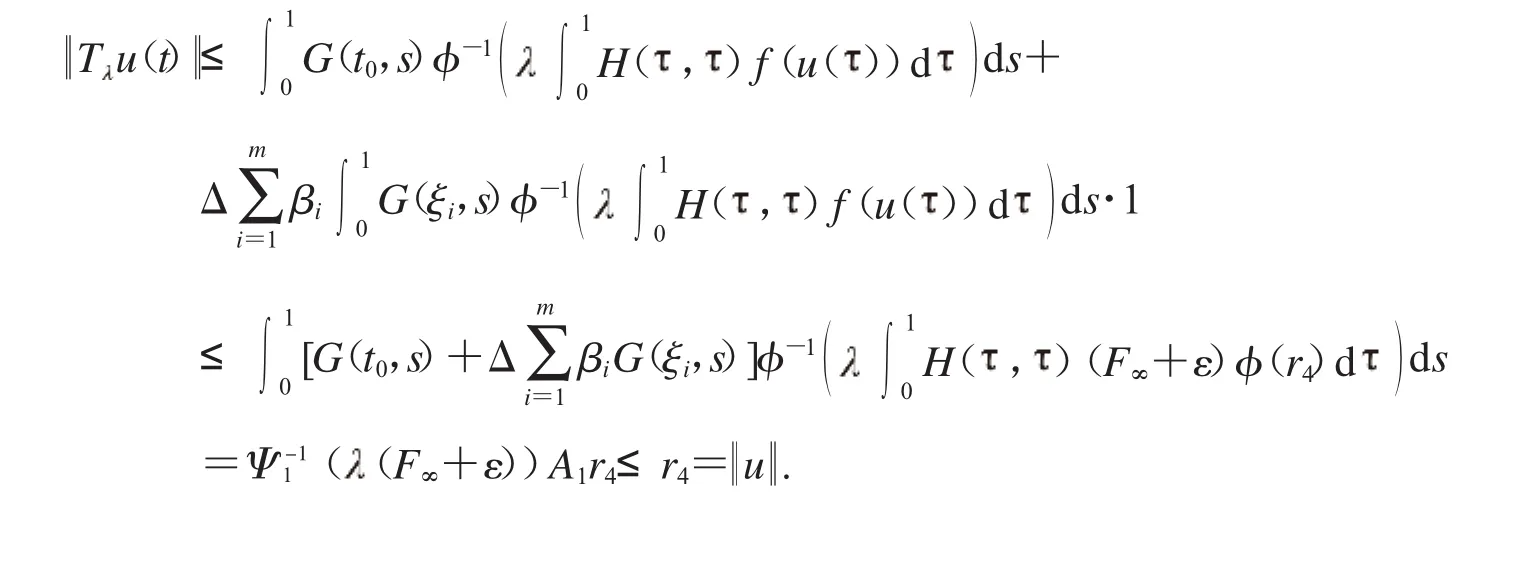
取Ω4＝{u∈Eu＜r4}有T u≤u ，當(dāng)u∈P∩?Ω4.

再由情況一和情況二可知，當(dāng)Ω2＝{u∈Eu ＜r2＝max{r3，r4}}，有

根據(jù)定理1.2.7和式（13）、（15）可知，T中有一個(gè)不動(dòng)點(diǎn)u∈P∩（Ω2Ω）1且滿足r1≤u≤r2，顯然u就是分?jǐn)?shù)階微分方程邊值問(wèn)題（1）的正解.證明完成.

2.1.3 假設(shè)r2＞r1＞0，有

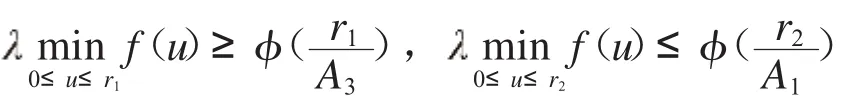
則分?jǐn)?shù)階微分方程（1）邊值問(wèn)題有一個(gè)正解u∈P且r1≤u ≤r2.

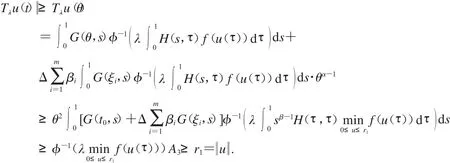
取Ω2＝{u∈Eu ＜r2}.當(dāng)u∈P∩?Ω2，有

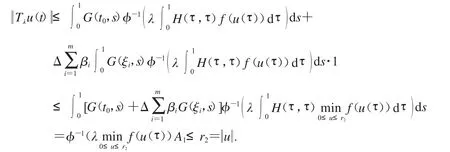
因此，由定理1.2.7知，分?jǐn)?shù)階微分方程（1）的邊值問(wèn)題有一個(gè)正解u∈P且r1≤u ≤r2.證明完成.

2.1.4 假設(shè)f0＝+∞，f∞＝+∞.那么對(duì)于∈（0，1），則分?jǐn)?shù)階微分方程（1）邊值問(wèn)題至少有兩個(gè)正解，其中

證明：令x（r）＝由f的連續(xù)性可知，x（r）∶（0，+∞）→（0，+∞）是連續(xù)的.

一方面，根據(jù)f0＝+∞，f∞＝+∞，可得limx（r）＝limx（r）＝0.故存在r0∈（0，+∞），使得x（r0）＝supx（r）＝1.對(duì)于∈（0，1），存在常數(shù)a1，a（20＜a1＜r0＜a2＜+∞）有

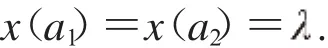
則，

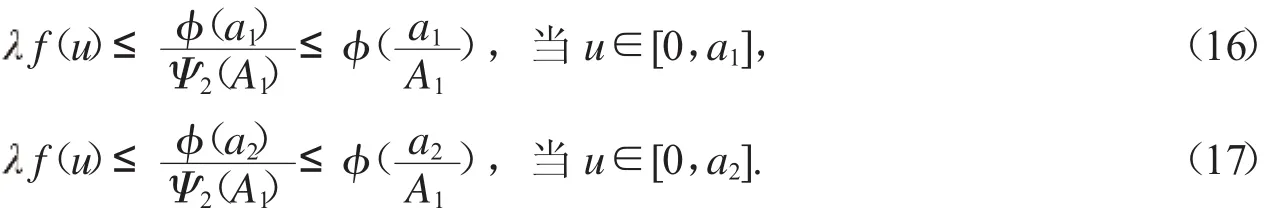
另一方面，根據(jù)f0＝+∞，f∞＝+∞，存在常數(shù)b1，b（20＜b1＜a1＜r0＜a2＜b2＜+∞）有

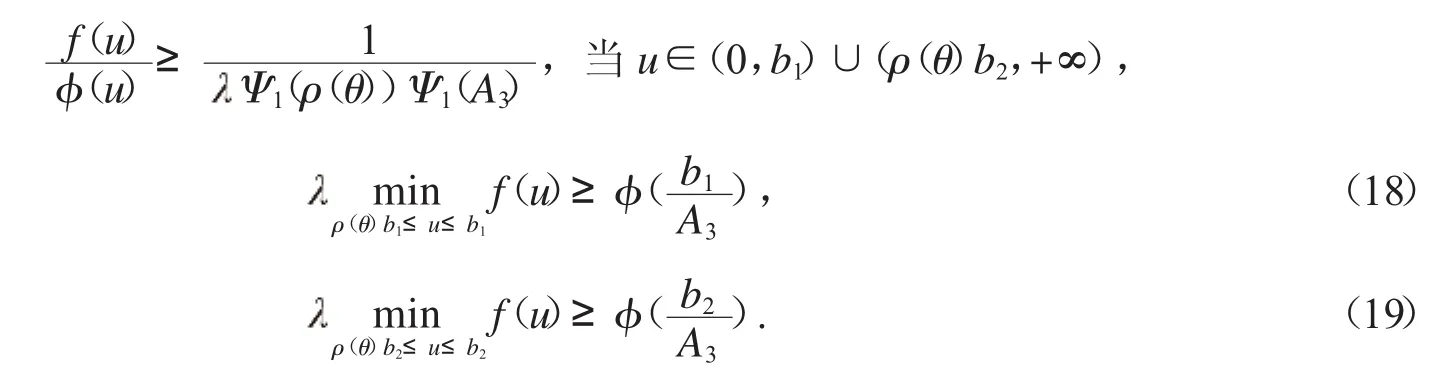
再由式（16）-（19）并根據(jù)定理2.1.3和定理1.2.7可得，當(dāng)∈（0，1）時(shí)，分?jǐn)?shù)階微分方程邊值問(wèn)題（1）至少有兩個(gè)正解.

2.2 正解不存在性定理的證明

2.2.1 假設(shè)F0＜+∞，F(xiàn)∞＜+∞.那么存在0＞0，0＜＜0，分?jǐn)?shù)階微分方程邊值問(wèn)題（1）無(wú)正解.

證明：根據(jù)F0＜+∞和F∞＜+∞可知，存在正常數(shù)M1，M2，r1，r2，使得當(dāng)r1＜r2時(shí)，滿足

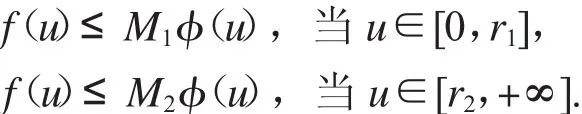
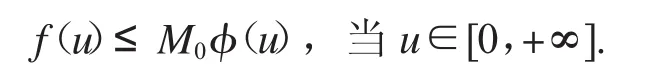
假設(shè)v（t）是分?jǐn)?shù)階微分方程邊值問(wèn)題（1）的正解.當(dāng)0＜＜0:＝M-01Ψ（1A-11），對(duì)于t∈[0，1]，有T v（t）＝v（t），因此有

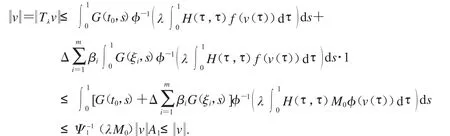
與T v（t）＝v（t）相矛盾，因此分?jǐn)?shù)階微分方程邊值問(wèn)題（1）無(wú)正解.證明完成.

2.2.2 假設(shè)f0＞0，f∞＞0.對(duì)于0＞0，＞0，分?jǐn)?shù)階微分方程邊值問(wèn)題（1）無(wú)正解.證明：根據(jù)f0＞0和f∞＞0，存在正常數(shù)m1，m2，r3，r4，使得當(dāng)r3＜r4，

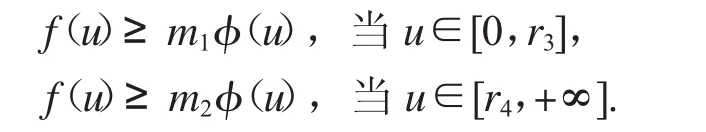
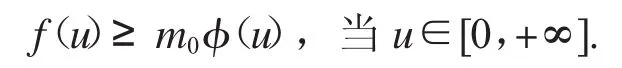
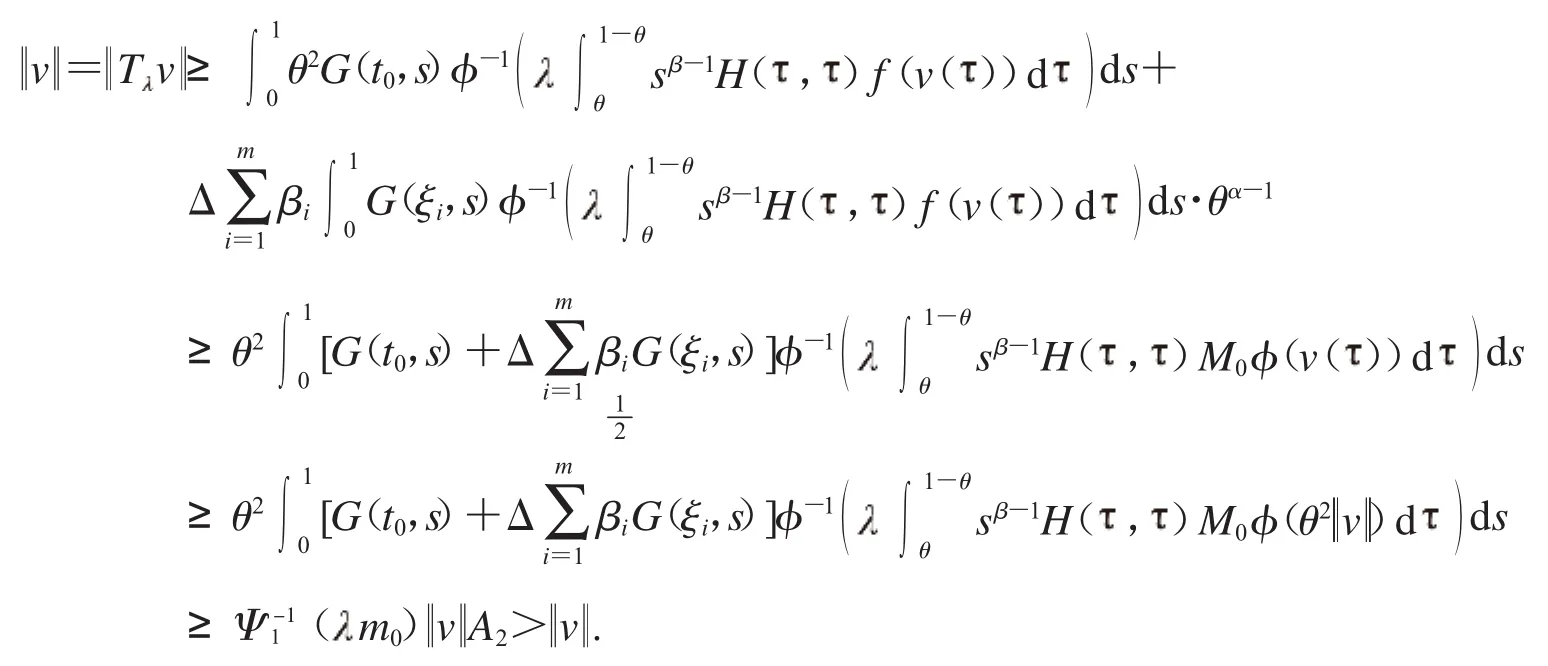
與T v（t）＝v（t）相矛盾，分?jǐn)?shù)階微分方程邊值問(wèn)題（1）無(wú)正解.證明完成.

3 例子

3.1 考慮邊值問(wèn)題：

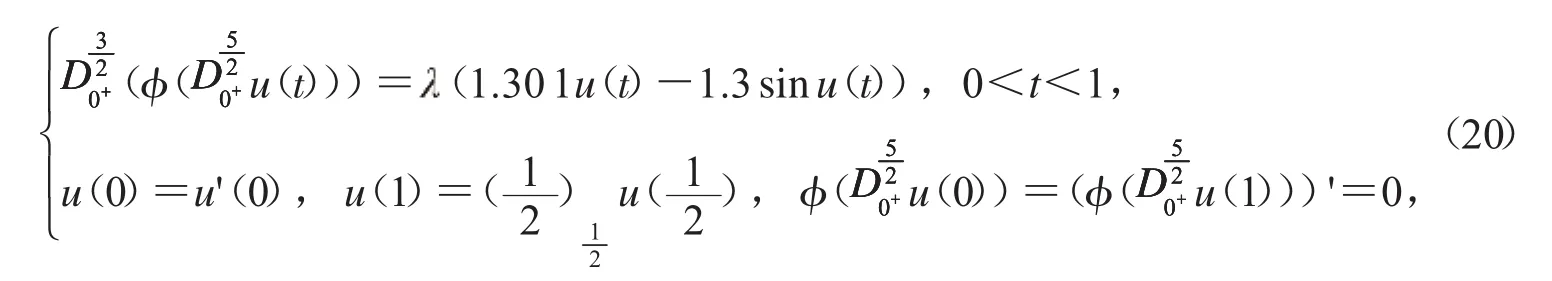
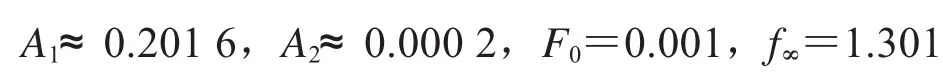
容易驗(yàn)證：f∞Ψ（1A-11）＞F0Ψ（2A-21）.因此，由定理2.1.1知，當(dāng)∈（3 843.197 5，4 960.3）邊值問(wèn)題（20）存在正解.

3.2 考慮以下邊值問(wèn)題：

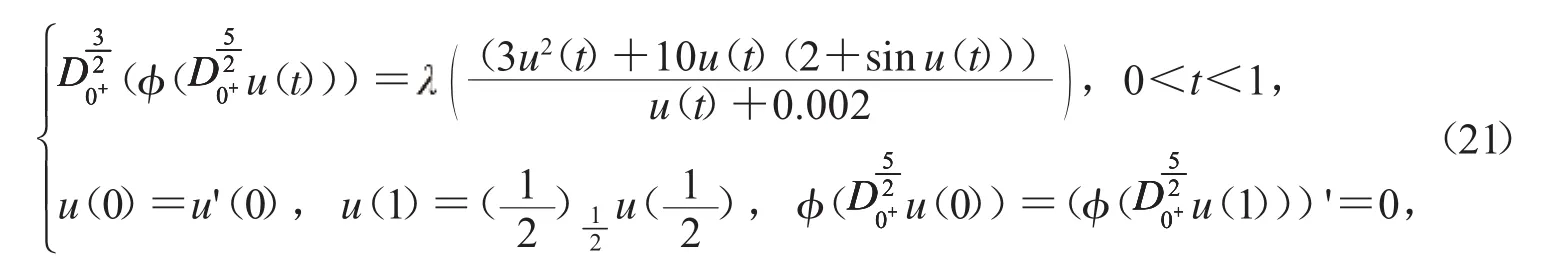
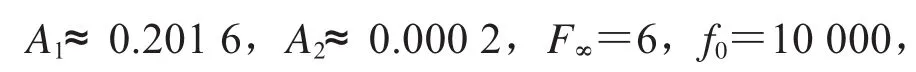
3.3 考慮以下邊值問(wèn)題：

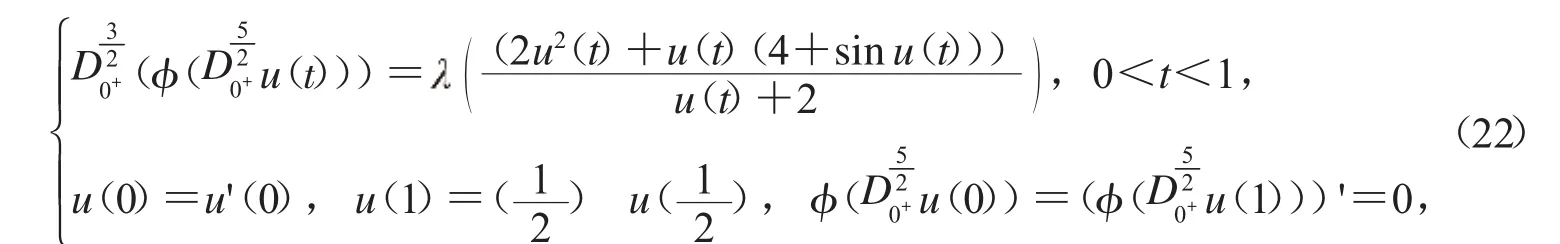
A1≈0.201 6，A2≈0.000 2，F(xiàn)0＝f0＝2，F(xiàn)∞＝10，f∞＝6并且u＜f（u）＜10u，

[1]MILLER K S，ROSS B.An introduction to the fractional calculus and fractional differential equation[M]. New York：Wiley-Interscience，1993.

[2]ROSS B.The fractional calculus and its applications，in：lecture notes in mathematics[M]//Lecture Notes in Mathematics.Berlin-New York：Springer-Verlag，1975.

[3]SAMKOSG，KILBASAA，MARICHEV O I.Fractional integrals and derivatives：theory and applications [M].Yverdon：Gordon and Breach，1993.

[4]KRASONSEL'SKIIMA.Positive solutionsofoperaterequations[M].Gronigen：PNoordhoff Ltd，1964.

[5]OLDHAMKB，SPANIERJ.Thefractionalcalculus[J].MathematicalGazette，1974，56（247）：396-400.

[6]BAI Z，Lü H.Positive solution for boundary value problem of nonlinear differential equation[J].Journal of Mathematical Analysis&Applications，2005，311（2）：495-505.

[7]ZHAO Y，SUN S，HAN Z，et al.The existence of multiple positive solutions for boundary value problems ofnonlinearfractionaldifferentialequations[J].CommunicationsinNonlinearScience&Numerical Simulation，2011，16（4）：2086-2097.

[8]CHEN T，LIU W，HU Z.A boundary value problem for fractional differential equation with p p math container loading mathjax-Laplacian operator at resonance[J].Nonlinear Analysis Theory Methods& Applications，2012，75（6）：3210-3217.

[9]HAN Z，LU H，ZHANG C.Positive solutions for eigenvalue problems of fractional differential equation with generalized p-Laplacian[J].Applied Mathematics&Computation，2015，257：526-536.

[10]NYAMORADIN.Existenceofsolutions for multi-point boundary value problems for fractional differential equations[J].Arab J Math Sci，2012，18（2）：165-175.

[11]MA D X.Positive solutions of multi-point boundary value problem of fractional differential equation[J]. Arab Journal of Mathematical Sciences，2015，21（2）：225-236.

[12]EL-SHAHEDM.Positivesolutionsforboundaryvalueproblemof nonlinear fractional differential equation [J].Abs Appl Anal，2007，2007：1-8.DOI：10.1155/2007/10368.

[13]WANG H.On the number of positive solutions of nonlinear systems[J].Journal of Mathematical Analysis &Applications，2003，281（1）：287-306.

[14]GUO D J，LAKSHMIKANTHAM V.Nonlinear problem in abstract cones[M].San Diego：AcademicPress，1988.

[15]SUN Y，ZHAO M.Positive solutionsfora classoffractionaldifferentialequations with integral boundary conditions[J].Applied Mathematics Letters，2014，34（1）：17-21.

[16]ZHAOY，SUNS，HANZ，etal.Theexistenceofmultiplepositivesolutionsforboundaryvalueproblems ofnonlinearfractionaldifferentialequations[J].Communications in Nonlinear Science&Numerical Simulation，2011，16（4）：2086-2097.

[17]XU X，JIANG D，YUAN C.Multiple positive solutions for the boundary value problem of a nonlinear fractional differential equation[J].Nonlinear Analysis Theory Methods&Applications，2009，71（10）：4676-4688.

[18]AVERY R，HENDERSON J.Two positive fixed points of nonlinear operator on ordered Banach spacea [J].Comm Appl Nonlinear Anal，2001，8（1）：27-36.

[19]BAIL，DAIB.Three solutionsfora p-Laplacian boundaryvalue problem with impulsive effects[J].Appl Math Comput，2011，217（24）：9895-9904.

[20]FENG M.JI D，GE W.Positive solutions for a class of boundary value problem with integral boundary conditions in Banach space[J].J Comput Appl Math，2008，222（2）：351-363.

[21]MA R，ZHANG J，F(xiàn)U S.The method of lower and upper solutions for fourth-order two-point boundary value problems[J].J Math Anal Appl，1997，215（2）：415-422.

Existence of Positive Solution for
Multi-Point Boundary Value Problems of FractionalDifferential Equations with p-Laplacian

ZHANG Yan,MA Dexiang
（College of Mathematics and Physics,North China Universityof Electrical Power,Beijing102206,China）

In the following multi-point boundary value problem of fractional differential equation with p-Laplacian:

fractional differential equation;p-Laplacian operator;multi-point boundary value problem;fixed point theorem

O175.1；O175.8

A

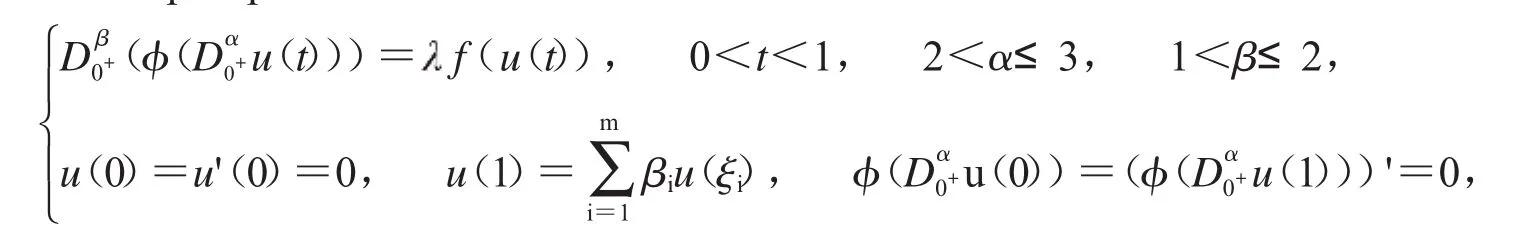
1001-4217（2017）03-0029-13

2016-09-21

張 艷（1991—），女，碩士研究生.研究方向：分?jǐn)?shù)階微分方程邊值問(wèn)題研究. E-mail：zhuanzhufadai@sohu.com