分?jǐn)?shù)Black-Scholes模型下美式亞式期權(quán)的近似定價(jià)法

林漢燕，袁 媛

（桂林航天工業(yè)學(xué)院理學(xué)部，廣西 桂林，541004）

分?jǐn)?shù)Black-Scholes模型下美式亞式期權(quán)的近似定價(jià)法

林漢燕，袁 媛

（桂林航天工業(yè)學(xué)院理學(xué)部，廣西 桂林，541004）

在分?jǐn)?shù)Black-Scholes模型下，首先應(yīng)用偏微分方程法簡(jiǎn)要推導(dǎo)具有固定敲定價(jià)格的歐式幾何平均亞式期權(quán)的定價(jià)公式，然后將標(biāo)準(zhǔn)Black-Scholes模型下美式期權(quán)定價(jià)的二次近似法推廣到美式亞式期權(quán)，得到具有固定敲定價(jià)格的美式幾何平均亞式期權(quán)價(jià)格的近似解析式.

分?jǐn)?shù)Black-Scholes模型；美式亞式期權(quán)；幾何平均；二次近似法

0引言

亞式期權(quán)是期權(quán)在到期日的收益依賴于整個(gè)有效期內(nèi)標(biāo)的資產(chǎn)價(jià)格平均值的合約.由于亞式期權(quán)是一種強(qiáng)路徑依賴型期權(quán)，所以可以避免投機(jī)者通過(guò)操縱標(biāo)的資產(chǎn)價(jià)格獲得暴利；另一方面，由于亞式期權(quán)比標(biāo)準(zhǔn)期權(quán)便宜，而且隨著時(shí)間增大，期權(quán)價(jià)格呈下降趨勢(shì)，所以對(duì)于某些公司亞式期權(quán)比標(biāo)準(zhǔn)期權(quán)更有吸引力.目前亞式期權(quán)在國(guó)際貿(mào)易、基金公司、保險(xiǎn)公司等金融領(lǐng)域應(yīng)用廣泛，很多學(xué)者對(duì)它的定價(jià)進(jìn)行了研究[1-4]，但這些成果都是針對(duì)標(biāo)準(zhǔn)Black-Scholes模型下的歐式亞式期權(quán)，美式亞式期權(quán)的研究很少.美式亞式期權(quán)是場(chǎng)內(nèi)外交易的重要期權(quán)之一，由于它具有美式期權(quán)的特點(diǎn)，可以在到期日前提前實(shí)施，但何時(shí)實(shí)施獲利最多未知，不能得到價(jià)格解的顯示表達(dá)式；同時(shí)又具有亞式期權(quán)的特點(diǎn)，所以定價(jià)顯得更復(fù)雜.目前美式亞式期權(quán)的研究成果有Ben-Ameur等用動(dòng)態(tài)規(guī)劃法研究美式亞式期權(quán)價(jià)格[5]；Hanse等在標(biāo)準(zhǔn)Black-Scholes模型下研究具有浮動(dòng)價(jià)格的算術(shù)平均和幾何平均的美式亞式期權(quán)價(jià)格的定價(jià)[6]；王旭等先利用Monte-Carlo模擬Black-Scholes模型下標(biāo)的資產(chǎn)的價(jià)格路徑，然后應(yīng)用偏最小二乘回歸法計(jì)算美式亞式期權(quán)價(jià)格[7]；孔文濤等在標(biāo)的資產(chǎn)價(jià)格服從跳躍-擴(kuò)散模型、利率遵循短期隨機(jī)利率模型的基礎(chǔ)上，應(yīng)用總體最小二乘擬蒙特卡羅方法為美式亞式期權(quán)定價(jià)[8]等.分?jǐn)?shù)Black-Scholes模型[9]是比標(biāo)準(zhǔn)Black-Scholes模型更接近股票運(yùn)動(dòng)特征的模型.在分?jǐn)?shù)Black-Scholes模型下，文獻(xiàn)[10]用擬條件期望法得到了浮動(dòng)價(jià)格的平均歐式亞式期權(quán)的定價(jià)公式；文獻(xiàn)[11]給出了基于可靠性思想的期權(quán)定價(jià)方法；文獻(xiàn)[12]應(yīng)用保險(xiǎn)精算法推導(dǎo)具有固定敲定價(jià)格的幾何平均歐式亞式期權(quán)的定價(jià)公式；文獻(xiàn)[13]應(yīng)用隨機(jī)分析理論討論亞式期權(quán)的定價(jià)；文獻(xiàn)[14]應(yīng)用偏微分方程法研究亞式期權(quán)的定價(jià).本文在分?jǐn)?shù)Black-Scholes模型下，對(duì)連續(xù)情形下具有固定敲定價(jià)格的幾何平均美式亞式期權(quán)的價(jià)格進(jìn)行研究.為下文敘述方便，首先用偏微分方程方法[14]簡(jiǎn)要推導(dǎo)歐式幾何平均亞式期權(quán)的定價(jià)公式.在這基礎(chǔ)上，將標(biāo)準(zhǔn)Black-Scholes模型下美式期權(quán)定價(jià)的二次近似法[15]應(yīng)用到美式亞式期權(quán)，得到期權(quán)價(jià)格的近似解析式.

1 基本模型

定義1設(shè)（Ω，F(xiàn)，R）是一個(gè)完備的概率空間，H∈（0，1），稱連續(xù)的高斯過(guò)程BH＝{B（Ht）；t≥0}是Hurst參數(shù)為H的分?jǐn)?shù)布朗運(yùn)動(dòng)，如果它滿足：

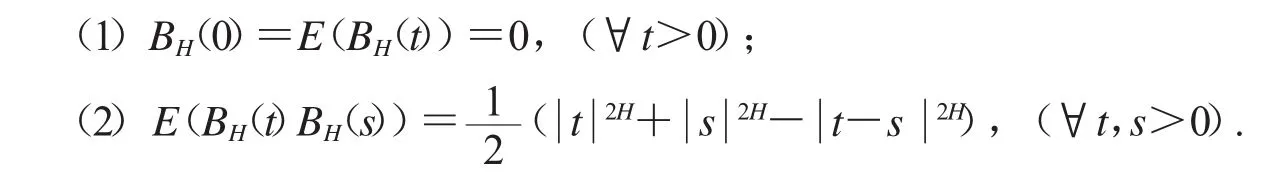
這里E表示關(guān)于概率測(cè)度P的期望.

分?jǐn)?shù)布朗運(yùn)動(dòng)的另一個(gè)重要性質(zhì)是具有自相似性，即對(duì)任意的H∈（0，1）和α＞0，B（Hαt）與αHB（Ht）有相同的有限維概率分布.本文討論Hurst參數(shù)1/2＜H＜1時(shí)的情形.

現(xiàn)假設(shè)金融市場(chǎng)僅有兩種資產(chǎn)，資產(chǎn)交易的額度和時(shí)間連續(xù)，交易時(shí)間為[0，T]，可以買空賣空，不存在交易稅收和費(fèi)用，借款和存款的利率相同.設(shè)第一種資產(chǎn)是連續(xù)支付紅利的風(fēng)險(xiǎn)資產(chǎn)，其價(jià)格S＝S（t）滿足分?jǐn)?shù)布朗運(yùn)動(dòng)：

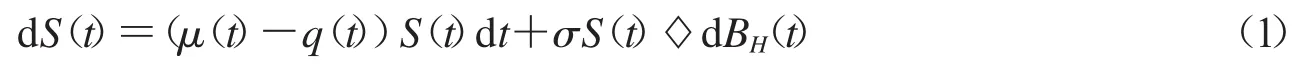
第二種資產(chǎn)是無(wú)風(fēng)險(xiǎn)證券，其價(jià)格A（t）滿足：

其中r（t）表示無(wú)風(fēng)險(xiǎn)利率，q（t）表示紅利率，σ≠0表示股價(jià)瞬時(shí)波動(dòng)率（常數(shù)），μ（t）表示股價(jià)期望回報(bào)率，B（Ht）表示分?jǐn)?shù)布朗運(yùn)動(dòng)，“◇”表示W(wǎng)ick積分.模型（1）、（2）稱為分?jǐn)?shù)Black-Scholes模型，并且是無(wú)套利的完全市場(chǎng)模型.

文獻(xiàn)[14]證明了分?jǐn)?shù)Black-Scholes模型下連續(xù)情形的具有固定敲定價(jià)格的歐式幾何平均亞式期權(quán)的價(jià)格F（t，J，S）滿足：

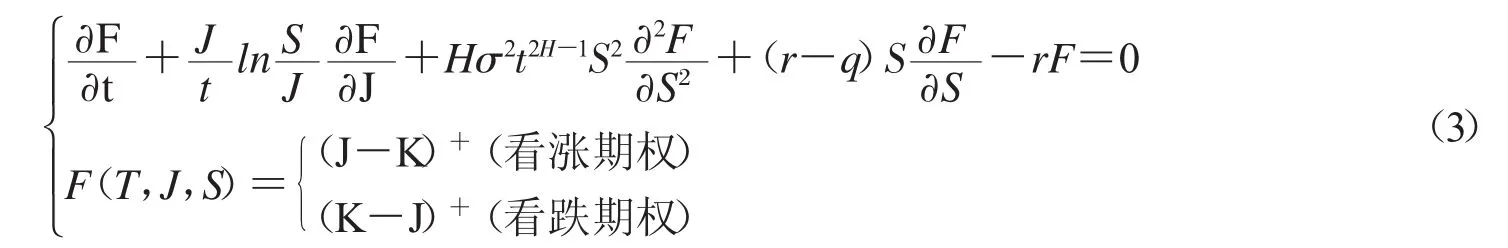
2 歐式具有固定敲定價(jià)格的幾何平均亞式期權(quán)的定價(jià)

定理1分?jǐn)?shù)Black-Scholes模型下無(wú)風(fēng)險(xiǎn)率為r，紅利率為q，波動(dòng)率為σ（r、q、σ均為常數(shù)），到期時(shí)間為T，執(zhí)行價(jià)格為K的具有固定敲定價(jià)格幾何平均亞式看漲期權(quán)在時(shí)刻t的價(jià)格c（t，J，S）為

類似得

定理2分?jǐn)?shù)Black-Scholes模型下無(wú)風(fēng)險(xiǎn)率為r，紅利率為q，波動(dòng)率為σ（r、q、σ均為常數(shù)），到期時(shí)間為T，執(zhí)行價(jià)格為K的具有固定敲定價(jià)格幾何平均亞式看跌期權(quán)在時(shí)刻t的價(jià)格p（t，J，S）為

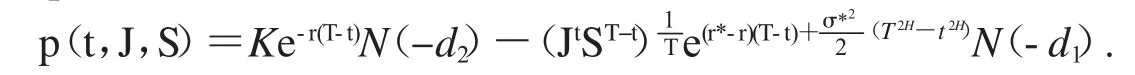
3 美式具有固定敲定價(jià)格的幾何平均亞式期權(quán)的近似定價(jià)

設(shè)e（ξ，t）＝e（t，J，S）（ξ同前）為t時(shí)刻美式亞式看漲期權(quán)價(jià)格的提前實(shí)施溢價(jià)，則e（ξ，t）＝U（ξ，t）-u（ξ，t），其中U（ξ，t）＝C（t，J，S）、u（ξ，t）＝c（t，J，S）分別為t時(shí)刻美式亞式看漲期權(quán)和歐式亞式看漲期權(quán)價(jià)格.U（ξ，t）適合定解問(wèn)題

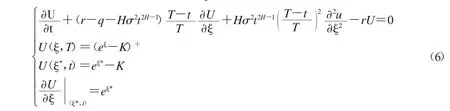
其中0＜ξ＜ξ*，0＜t＜T，ξ*表示美式亞式看漲期權(quán)的最佳實(shí)施邊界.顯然e（ξ，t）滿足方程

令e（ξ，t）＝h（φ）g（ξ，h（φ）），其中h＝h（φ）、φ＝φ（t）待定，且φ（t）滿足φ（T）＝0，上式可化為

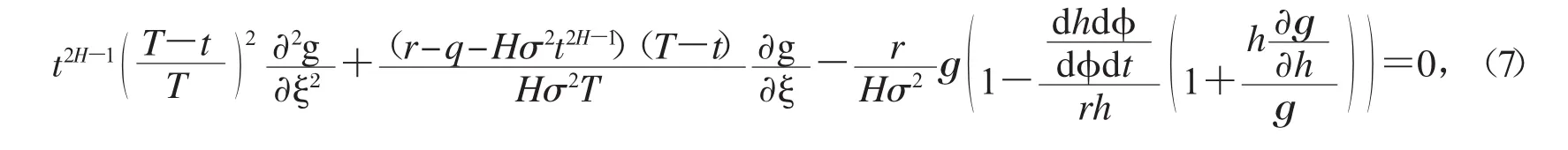
由此得

定理3分?jǐn)?shù)Black-Scholes模型下無(wú)風(fēng)險(xiǎn)率為r，紅利率為q，波動(dòng)率為σ（r、q、σ均為常數(shù)），到期時(shí)間為T，執(zhí)行價(jià)格為K的具有固定敲定價(jià)格幾何平均美式亞式看漲期權(quán)在t時(shí)刻價(jià)格C（t，J，S）為

類似得

定理4分?jǐn)?shù)Black-Scholes模型下無(wú)風(fēng)險(xiǎn)率為r，紅利率為q，波動(dòng)率為σ（r、q、σ均為常數(shù)），到期時(shí)間為T，執(zhí)行價(jià)格為K的具有固定敲定價(jià)格幾何平均美式亞式看跌期權(quán)在t時(shí)刻價(jià)格P（t，J，S）為

4 結(jié)論

本文在分?jǐn)?shù)Black-Scholes模型下用二次近似法推導(dǎo)了連續(xù)情形的具有固定敲定價(jià)格美式亞式期權(quán)定價(jià)的近似公式.公式形式與Black-Scholes模型下標(biāo)準(zhǔn)美式期權(quán)定價(jià)的近似公式相似.

[1]戴民.路徑依賴期權(quán)二叉樹方法的數(shù)值分析[D].上海：復(fù)旦大學(xué)，2002.

[2]姜禮尚.期權(quán)定價(jià)的數(shù)學(xué)模型和方法[M].北京：高等教育出版社，2003.

[3]周清，李超.分?jǐn)?shù)Vasicek利率模型下幾何平均亞式期權(quán)的定價(jià)公式[J].應(yīng)用數(shù)學(xué)學(xué)報(bào)，2014，37（4）：662-675.

[4]CAO G L，WANG Y.Risk-neutral pricingforgeometric average Asian option with floatingstrike[J].Journal of University of Chinese Academy of Sciences，2015，32（1）：13-17.

[5]BEN-AMEURH，BRETONM，L'ECUYERP.Adynamicprogramming procedure for pricing American-style Asian option[J].Management Science，2002，48（5）：625-643.

[6]HANSEN A T，JORGENSEN P L.Analytical valuation of American-style Asian option[J].Management Science，2000，46（8）：1116-1136.

[7]王旭，王拉省.偏最小二乘回歸在美式-亞式期權(quán)定價(jià)中的應(yīng)用[J].紡織高校基礎(chǔ)科學(xué)學(xué)報(bào)，2008，21（1）：24-130.

[8]孔文濤，張衛(wèi)國(guó).帶跳市場(chǎng)中隨機(jī)利率下的美式-亞式期權(quán)定價(jià)[J].系統(tǒng)工程學(xué)報(bào)，2012，27（3）：338-342.

[9]ANDELBROTB.Long-runlinearity，locallyGaussianProcesses-spectraand infinity variance[J].International Economic Review，1969，10（1）：2-111.

[10]沈明軒，何朝林.分?jǐn)?shù)布朗運(yùn)動(dòng)環(huán)境中幾何平均亞式期權(quán)的定價(jià)[J].山東大學(xué)學(xué)報(bào)理學(xué)版，2013，48（3）：48-52.

[11]孫玉東，師義民，譚偉.分?jǐn)?shù)布朗運(yùn)動(dòng)環(huán)境下亞式期權(quán)定價(jià)的新方法[J].工程數(shù)學(xué)學(xué)報(bào)，2012，2（2）：173-178.

[12]周銀，杜雪樵.分?jǐn)?shù)布朗運(yùn)動(dòng)下的亞式期權(quán)定價(jià)[J].合肥工業(yè)大學(xué)學(xué)報(bào)（科學(xué)版），2011，34（2）：317-320.

[13]裴曉芬，馮德成.分?jǐn)?shù)布朗運(yùn)動(dòng)下帶紅利的亞式期權(quán)定價(jià)的新解法[J].河北師范大學(xué)學(xué)報(bào)（自然科學(xué)版），2014，38（2）：123-128.

[14]武文娜，周圣武，黎偉.分?jǐn)?shù)布朗運(yùn)動(dòng)下支付紅利的亞式期權(quán)定價(jià)[J].河南科技大學(xué)學(xué)報(bào)（自然科學(xué)版），2012，33（4）：100-104.

[15]BARONE-ADESIG，WHALEY R E.Efficientanalytic approximation of American option values[J].The Journal of Finance，1987，42（2）：301-320.

American-Style Asian Option Pricing in the Fractional Black-Scholes Model

LIN Hanyan,YUAN Yuan
（Guilin Universityof Aerospace Technology,Facultyof Science,Guilin 541004,Guangxi,China）

The formulas of the European-style geometric average Asian option with fix strike price by partial differential equation method in the fractional Black-Scholes model are derived. Based on the formulas,the classical quadratic approximation in the standard Black-Scholes model is applied to the pricing of American-style Asian option.The approximate formulas of American-style geometric average Asian option with fix strike price are obtained.

fractional Black-Scholes model;American-style Asian option;geometric average; quadratic approximation

O211.6；F830.9

A

1001-4217（2017）03-0015-07

2016-09-02

林漢燕（1973—），女，漢族，廣西貴港人，碩士，副教授，研究方向：金融數(shù)學(xué). E-mail：linhanyan2006@163.com

廣西教育廳科研項(xiàng)目（YB2014436）.