在“想不到”中演繹課堂別樣精彩

溫勝楠+鐘世文

【摘 要】小學生的“已知”，往往只是表面的“已知”。他們對這個結論是如何生發(fā)的，并沒有深入思考。另外，個別學生的“已知”，并不能代表全體學生的“已知”。因此，教師只有深入分析學生“已知”背后的“未知”，深度挖掘學生“想不到”的東西，才能生動演繹數學課堂的別樣精彩。

【關鍵詞】巧妙設問 另類測量 順學而導

學生都“知道”了，課該怎么上？這是廣大一線數學教師經常遇到、倍感糾結和亟待解決的問題。顧志能老師執(zhí)教的“三角形的內角和”一課，就這一問題在如何直面應對、尋求對策、突破瓶頸和走出困境等方面做了大膽的探索和積極的嘗試。他以學生“想不到”的導入方式來引發(fā)學生的測量需要，以學生“想不到”的測量方式來激活學生的測量熱情，以學生“想不到”的接納方式來點燃學生的驗證激情……這樣通過深度挖掘看似學生都“已知”但卻“想不到”的東西，生動演繹了數學課堂的別樣精彩。現采擷三個教學片段，與同人們一起賞析。

一、巧妙設問：以學生“想不到”的導入方式，引發(fā)學生的測量需要

【片段一】

師：關于三角形的內角和，你們已經知道了什么？

生：三角形的內角和是180°。

生：我們老師說過，三角形內角和永遠都是180°。

生：三角形不管什么形狀，不管什么大小，內角和永遠都是180°。

（全班學生沒有一個不舉手的，回答問題時還略有不屑）

師：有這樣的結論？真的嗎？我不信！

師：（課件出示圖 1）請看大屏幕，這個三角形的內角和是多少度？

生：180°。

師：現在，如果在這個三角形中添一條線，想一想，它會是什么樣子呢？（出示圖 2）現在將它們分開（出示圖 3），現在這兩個小三角形的內角和又分別是多少度了呢？

（學生有說 90°的，瞬間又改口說 180°；也有學生說 180°，但顯然“口氣不硬”）

師：一個大三角形內角和是 180°，現在分成了兩個小三角形，每個小三角形內角和還是 180°？真的嗎？我不信！你有什么辦法說服我？

生：老師，那我們量一量，看看到底是多少度。

……

【評析】在上述教學片段中，顧老師直面學生的“已知”——三角形不管什么形狀，不管什么大小，內角和永遠都是 180°，開門見山，直奔課題。通過兩次巧妙設問，以學生“想不到”的導入方式，引發(fā)學生的測量需要。一是面對學生自恃對即將學習內容“已知”的不屑之情，教師拋出“有這樣的結論？真的嗎？我不信！”之問；二是依托將一個大三角形一分為二成兩個小三角形的圖形變式，針對學生處于“底氣不足”之時，教師再次表達“疑惑心理”——“真的嗎？我不信！你有什么辦法說服我？”從而水到渠成地促發(fā)學生主動提出“老師，那我們量一量，看看到底是多少度”的測量需求。由此像呼吸一樣自然地引發(fā)了學生主動進行測量的實踐行動，讓學生自覺經歷內角和這個知識形成的必由過程——測量計算。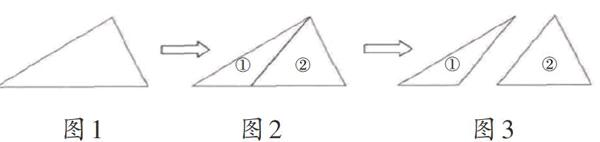

二、另類測量：以學生“想不到”的測量方式，激活學生的測量熱情

【片段二】

師：老師這里有一個很特別的量法，你們想不想知道老師是怎樣測量的嗎？

師：好！現在，我可要比一比、看一看哪位同學的小眼睛最亮！小腦袋最靈！

（借助學生的一個三角形，在實物展臺上邊演示邊講解如下過程，如圖4。重點是讓學生看懂鉛筆的轉動，實際就是在依次“測量”三個內角）

師：請同學注意觀察啦，現在鉛筆的筆尖朝哪個方向？我現在測量的是哪個角？現在呢？現在呢？現在筆尖卻變成朝哪個方向啦？跟開始正好怎么樣啦？（正好相反）

師：筆尖原來朝著右邊的，“量”了三個角之后，朝著左邊了。由此，你們想到了什么角？也就是說，我們可以把它看作是繞著鉛筆有橡皮擦的一端旋轉了幾周？是多少度？這說明，這三個角的度數之和是多少呢？——180°。

師：你們想不想也來用這種方法試量一下？

教室里一陣“騷動”，每個學生都迫不及待地開始了這樣的測量……

【評析】在上述教學片段中，顧老師抓住“人人都有對新鮮事物感興趣”的心理特征，將學生“已知”的測量方法（用量角器量）進行“改頭換面”，以“新”的、學生“想不到”的測量方法（轉鉛筆）取而代之，讓學生產生陌生感、新奇感，引起學生有意注意，促使產生迫切想知道教師是怎樣使用鉛筆進行測量的心向。此時此刻，學生個個小眼睛發(fā)亮，人人小腦袋飛轉，都在思考“這又是怎么回事呢？”在明白轉鉛筆測量的原理之后，“每個學生都迫不及待地開始了這樣的測量”，從而有效激活了學生的測量熱情。

三、順學而導：以學生“想不到”的接納方式，點燃學生的驗證激情

【片段三】

師：如果不量，不轉鉛筆，你還有什么辦法，可以檢驗你手頭的三角形的內角和是不是180°嗎？請每人獨立思考。

生：（良久）老師，我有個辦法，就是有點殘忍，不知道行不行？

師：好，那就請上來介紹一下你所謂“殘忍”的方法吧。

生：我把三角形的三個角撕下來，剛好可以拼成一個平角，所以三角形的內角和是180°。

師：撕的時候要注意什么？拼的時候又要注意什么？

生：我先把三個內角分別標上序號，然后撕下來，撕的時候要保留每個角的邊和頂點，拼的時候要把角的頂點重合，邊也要重合。

師：你是怎么知道拼成的是平角？

生：我用直尺驗證了，角的兩邊呈一條直線。

師：誰來點評他的方法？

生：這樣撕拼，很快。

生：我覺得他的做法挺實用的。

師：他居然敢把角撕下來去拼，膽子真的夠大！的確，有些發(fā)明創(chuàng)造往往就是從破壞開始的！

師：同學們，你們想不想“殘忍”一把？

熱烈的氣氛再度上演……

【評析】在上述教學片段中，顧老師首先提出“如果不量，不轉鉛筆，你還有什么辦法，可以檢驗你手頭的三角形的內角和是不是180°嗎？”這一問題，讓學生進行獨立思考。良久，有學生怯生生提出了“殘忍”的方法，之所以說“殘忍”，是因為學生從未經歷過把學具先搞壞再利用的操作活動。學生“想不到”教師居然這么爽快地接納了他的想法，并要求自己上臺現場演示。接著，教師順著學生的思路，圍繞“撕拼”細節(jié)引導學生思考“撕的時候要注意什么？拼的時候又要注意什么？”“你是怎么知道拼成的是平角？”等一連串問題，在師生、生生智慧的對話和思維的碰撞中，所有學生都覺得心中“癢癢”的，迫切也想“殘忍”一把，由此動手實踐驗證的激情再度上演。

總之，一節(jié)看似學生都“已知”的課，就是需要這樣的“想不到”。小學生的“已知”，往往只是表面的“已知”，僅僅聽到或看到了某個數學的結論而已。他們對這個結論是如何生發(fā)的，并沒有深入思考。況且個別學生的“已知”，并不能代表全體學生的“已知”。因此，教師只有深入分析學生“已知”背后的“未知”，深度挖掘學生“想不到”的東西，才能生動演繹數學課堂的別樣精彩。

（福建省上杭縣實驗小學 364200）