關于正則點的兩個性質

廣東省英德市西牛鎮沙壩小學 (513028) 劉京培

關于正則點的兩個性質

廣東省英德市西牛鎮沙壩小學 (513028) 劉京培

文(1)給出了正則點的定義：在ΔABC中，若點Z滿足AZ·BC=BZ·CA=CZ·AB,則此點稱為正則點.

性質1 如圖1，O、H、F、Z分別為ΔABC的外心、垂心、費馬點和正則點，則有FZ∥OH.

圖1

證：如圖1，以AB為邊向外作正ΔABM，頂點為M，連接CM,得C、F、M三點共線，且交OH于點P，連接OM交AB于點D，易得OM垂直平分AB，延長CZ

交OH于點Q,延長CH交AB于E.因為O、H互為等角共軛點，文[1]給出了F、Z互為等角共軛點，有∠BCO=∠ACH，∠BCZ=∠ACF，所以易得∠OCZ=∠HCF，∠OCF=∠HCQ.又CE⊥AB，OM⊥AB，得CE∥OM，∴∠HCF=∠OMC.

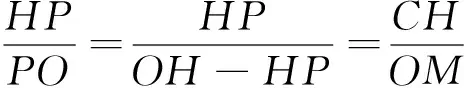
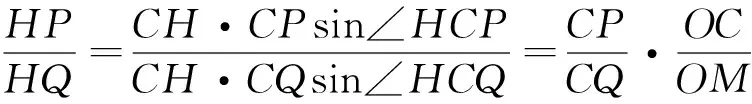
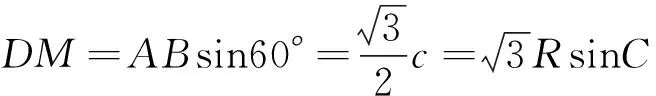
由等比性質知，FZ∥OH.

性質2 圖與符號同上，若G為重心，則有

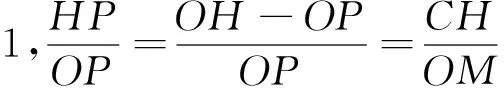
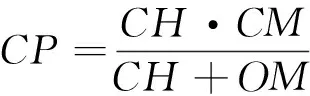
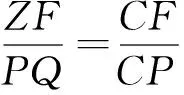
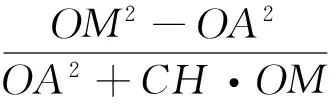
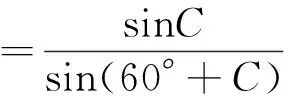
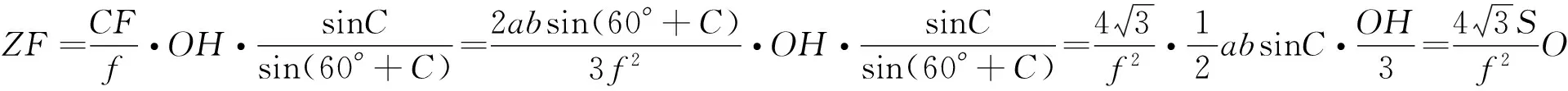
[1]沈文選,湯春桃.幾何瑰寶[M].哈爾濱：哈爾濱工業大學出版社，2014：380-393.