讓“教”與“學”不再“唱雙簧”
李蕓
[摘 要]“用字母表示數”這一課是學生首次正式接觸代數領域的內容,標志著學生的思維由算術空間正式進入代數空間,其重要性不言而喻。通過“在不疑處設疑”“在存疑處釋疑”“在釋疑后釋放”,對“用字母表示數”的教學設計進行改進與思考,實現教與學的有效互動。
[關鍵詞]代數;字母;教學設計;教與學
[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068(2017)17-0036-01
學習代數知識前,學生已充分掌握各種運算律,對常見數量關系等基礎知識也非常熟悉。通過用字母代表數,用含有字母的代數式進行運算并借此表述各種等量關系,可為以后學生學習方程做好鋪墊。由數字運算一下子過渡到字母運算,學生思維節奏往往會跟不上。因此,幫助學生正確理解與認識代數式的意義與先進性,是本單元教學的重點。
一、在不疑處存疑
師(出示課本例2):例題中的英文字母b代表什么?具體可以是什么數字?
生1:表示已走的行程,大小介于0~280之間。
師:那280~b這個式子又代表什么?
生2:代表剩下的行程。
師:如果再選用一個英文字母“c”代表剩下的行程,你能用含有b和c的式子表示它們之間的數量關系嗎?
生3:c=280-b。
師:因此我們可以下結論,單獨一個字母可以代表一個數,放入等式中可以表示數量關系。
由此可知,字母既可以代表數字,也可以代入等式表示數量關系。不過,此處存在兩點疑問:
第一,“b”是個“未知數”,用“280-b”表示解題結果,實際上結果仍是未知的。這也正是算術空間與代數空間的不同之處,算術是為了確定結果的數值,代數往往只是揭示內部規律。
第二,教材中,例1到例2就由離散量忽然轉向連續量,會引起學生質疑:既然用含有字母的代數式表示解題結果比數字更管用,那學數字計算還有什么用?看來,問題的癥結不在于運算結果換了一個表達形式,而在于字母的不確定性帶來的更為廣闊的思考空間。
二、在存疑處釋疑
出示:北京、天津兩城的地鐵站間的距離為280千米。一輛地鐵從北京開往天津,已行駛一段距離,剩下的路程是( )千米。
師:總路程、已行駛的路程、未行駛路程這三者之間的關系你能用線段圖表示出來嗎?
生1:我把總路程一分為二,一段表示已行駛路程,一段表示未行駛路程。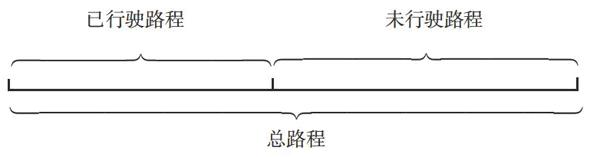
師:在這里,已行駛路程知道是多少千米嗎?
生2:題目沒有交代。但是,不論它是多少,我們都能利用“總路程-已行駛路程=未行駛路程”這個公式求出來。
生3:我用字母 b代表已行駛路程,未行駛路程程則用(280-b)表示。
教學改進后,教師沒有刻意讓學生用式子表示運算結果,而是引導他們先用語言文字表述數量關系并將三者之間的關系用線段圖表示出來。學生的主觀能動性被這一開放的活動情境有效激發出來了,他們不僅會根據數量關系進行具體的數值運算,而且會借助簡明扼要的文字式來直觀反映數量關系,部分學生還能自主地采用字母來表示未知變量,并順理成章地想到用代數式“280-b”表示剩下的路程。
三、在釋疑后釋放
回顧“用字母表示數”一課的改進歷程,無論多么基礎的知識內容,我們都要不斷探本求源,研磨出貼合學生的課堂互動環節,力求讓“教”與“學”自然發生,使離學生感知經驗較遠的知識能在學生頭腦中生根。
數學學習的主體永遠是學生,教師的職責只是教學的設計者、主持者、組織者和引導者。教師要想方設法把學生學習的積極性和主動性調動起來。數學活動的主要形式是全員(包括師生、生生)互動,而保證互動有效性的正是能促進思維發展的一系列問題。現實性與趣味性是數學教學中選擇問題情境的重要標準。教師不但要學會做教學設計的加法,更要學會做教學設計的減法,只有把形式主義趕出去,才能釋放出更多創新的活力與空間。
(責編 羅 艷)

