運用有效策略發展形象思維

孫保華

【摘 要】小學生的數學思維特點，是以數學形象思維為主要形式逐步過渡到以抽象邏輯思維為主要形式，但這種抽象邏輯思維仍然與感性經驗直接相聯系。這就是說，小學生的思維活動是以形象思維為先導的，而且在進行邏輯思維時，仍然與形象思維密切聯系的。對此，在日常教學實踐中，教師應通過若干策略來培養學生的數學形象思維。

【關鍵詞】形象思維 教學策略

形象思維不僅有助于學生理解數學知識的形成過程，而且有助于培養學生的空間觀念和幾何直觀能力。因此，在小學階段要重視學生形象思維的培養，為他們抽象思維的發展打好基礎。

小學生的思維特點正處于由形象思維向抽象思維過渡的階段，在數學學習中形象思維可以起到線索誘導和啟發靈感的作用。因此，在教學中我們應運用有效策略，促進學生數學形象思維的發展。

一、挖掘教材，直觀表征

數學中的概念、性質、法則和公式等比較抽象，同時學生在學習中以直觀形象思維為主，因此，根據實際教學的需求，我們應充分挖掘教材，盡可能地借助直觀表征幫助學生更好地進行數學學習，以提高學生的數學形象思維。

（一）簡圖

例如，教學兩位數乘一位數14×2 的口算時，使學生知道先算2個十得20，再算2個4得8，最后把兩次乘積相加得28。在這樣的感知活動中，就獲得了算法，明確了算理。然后在原式上初步概括，并一邊畫簡圖一邊引導學生計算：

再通過如上同一形式的幾道題的練習，在學生頭腦中形成了算法的圖式表象，如：

最后概括出兩位數乘一位數的口算方法。

（二）表格

表格也是直觀表征的方式。一方面，表格可以用于整理信息。例如，蘇教版四年級上冊中解決買筆記本的實際問題時，出示教材提供的表格，要求學生利用表格整理條件和問題，這樣可以使信息和數據更加清晰、直觀，能幫助學生更好地分析數量關系。

另一方面，有些實際問題也可以通過列表的方式展現解答的思路和過程。例如，蘇教版六年級下冊中解決租船的實際問題時，借助列表的直觀表征方法幫助學生將不同的方案一一列舉出來（如圖2），滲透了不重復不遺漏、有序思考的思想，從中一目了然地找到了解決問題的方案。

（三）線段圖

線段圖是由幾條線段組合在一起，用來表示實際問題中的數量關系，幫助我們分析題意從而解答問題的一種平面示意圖。借助線段圖，可以將信息以及復雜的關系直觀呈現，使學生經歷從抽象的文字到直觀的再創造，學會數學表達，找到解決問題的方法。例如：

總之，這些直觀表征對提高學生分析、解決問題的能力，積累解決問題的經驗有非常重要的作用。

二、充分感知，積累表象

表象是客觀事物經過主體感知以后在頭腦中所留下的形象。表象是對過去經歷過的東西進行概括的結果，它既以直觀的形象反映現實，又具有一定的概括性。表象是形象思維的材料，沒有表象的活動就沒有形象思維，所以正確、豐富的表象積累，是進行形象思維的基礎。

（一）借助演示，積累表象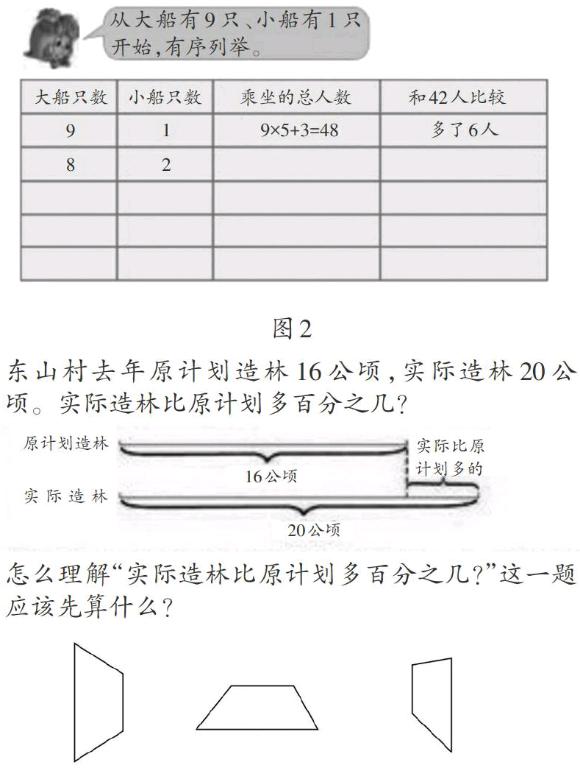

在教學過程中，教師運用圖片、實物和信息技術手段輔助教學，把抽象知識形象化，讓學生充分觀察、比較所學的材料，建立數學概念的表象，增強數學表象的直觀性。如認識圓柱體時，可以通過形式多樣的圓柱體實物或信息技術手段給學生觸摸和觀察的機會，建立圓柱體的表象。

（二）引導操作，積累表象

動手操作能使學生多種感官都參與到學習中來，從而在頭腦中建立形象，積累表象。如教學平行四邊形的面積時，先讓學生在硬紙板上畫一個平行四邊形，再讓學生沿著高剪開拼一拼，看一看拼成的圖形，幫助學生建立起平行四邊形拼成長方形的表象。

（三）指導默想，積累表象

沒有形象記憶，就不可能有表象積累。只有讓學生將感受到的直觀形象在腦子中進行“回憶”，通過默畫、默述、默記、默想等手段，才能逐漸強化。如教學體積單位時，教師讓學生拿出體積是1立方分米的正方體，通過看一看、摸一摸 、比一比，再讓學生閉眼想一想，從而將1立方分米的大小立體地印在了頭腦中。

三、數學“直感”，特征判別

在數學學習中，學生對于事物的形象識別，常用帶有普遍性的概括表象去對照個別特性的具體形象，并加以判斷，是一種整體形象的分解與整合的直觀感知過程。這種活動往往不以概念為中介，而一般以原儲存在大腦中的表象記憶為對照依據。所以數學直感是在數學表象的基礎上對有關數學形象的特征判別。

（一）形象識別“直感”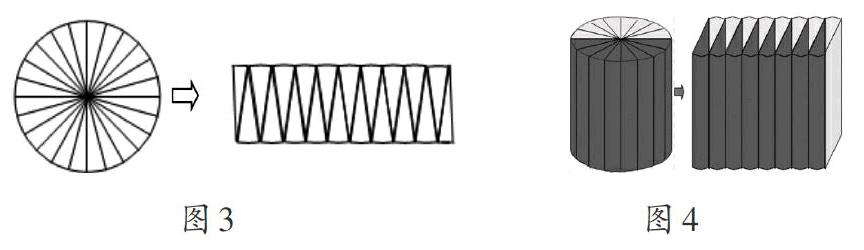

它是用數學表象的特征去比較具體對象以判明該對象是否與有關表象同質。形象識別直感主要表現于各種圖形、圖式在變式情況下的再認，以及在復合、綜合形態下的分解辨認。

例如，指出下圖所示圖形是不是屬于梯形？就是根據已有圖形表象進行形象識別。

（二）形象相似“直感”

當形象識別找不到同質的已有表象時，可通過最接近于目標形象的已有表象進行形象識別，比較異同，再作適當的思維加工，找到目標形象與已有表象的聯結關節，最后解決問題。

例如，圓柱體體積公式可通過類似圓面積公式的推導方法得出。其形象思維的過程如下：圓面積公式是通過將圓劃分成一個個小扇形，再拼成長方形后導出的。通過推導，學生頭腦中建立了圖形表象（圖3）。那么圓柱體體積公式如何推導呢？通過分析，如果把圓看成有一定厚度的圓形，那么就是圓柱體，于是找到了兩者的聯結關節，圓柱體體積也可以仿照推導圓面積公式的方法求得（圖4）。

四、合理想象，激發靈感

愛因斯坦指出：“想象力比知識更重要，想象力是科學研究中的實在因素，是知識進化的源泉。”想象是在頭腦中對已有表象經過組合和改造，產生新表象的思維過程。想象是以表象為基礎，以直感為手段產生新的表象。因此在教學中要給學生想象的空間和機會，激發其產生靈感。

1.圖形想象是以已有的幾何圖形表象為基礎，通過直感對其進行加工和改造，產生新表象的過程。一般認為，圖形想象包括圖形構想、圖形表達、圖形識別和圖形推理四個層次。如在面臨“邊長為20米的正方形草地的一角上有根木樁，用繩子拴著一只羊，已知繩長等于正方形邊長的一半，求羊吃不到草的草地面積”這樣的問題情境時，學生根據情境在頭腦中反映出正方形，并對羊能達到的最遠的地方進行圖形構想，然后進行圖形表達，畫出相應的草圖，完成圖形表達進入圖形識別。即發現羊能達到的部分是以正方形的頂點為圓心，半徑為10米，圓心角為90°的扇形。完成圖形識別后便可進入圖形推理，即發現羊吃不到草的草地面積為正方形面積與扇形面積的差，至此完成圖形推理。

2.圖式想象是以已有的圖式為基礎，通過直感對其進行加工和改造，產生新的表象的過程。圖式想象也包括圖式構想、圖式表達、圖式識別和圖式推理四個階段。如對于“李阿姨買了5千克蘋果，共花了30元，每千克蘋果需要多少元？”這一問題，學生根據問題情境，構想出5千克和30元之間的除法關系，完成圖式構想，進入圖式表達，即寫出算式30÷5。根據圖式表達，學生明確是整數除法，完成圖式識別進入圖式推理，即完成除法計算得出答案。

總之，在數學教學中，我們要依據學生認知心理發展的規律，充分挖掘教材中的素材，讓形象進入知識發生、發展的過程，嘗試運用多種策略去開拓學生的形象思維能力，強化學生運用形象思維的習慣，有意識地進行形象思維能力的培養。

參考文獻：

[1]李光樹.小學數學學習論[M].北京：人民教育出版社，2014.

[2]汪繩祖.小學數學教育學[M].北京：高等教育出版社，2000.

[3]張興華.兒童學習心理與小學數學教學[M].江蘇：江蘇教育出版社，2011.

[4]陳曦.借助直觀表征培養數學思維能力[J].小學數學教育.2016（9）.

（江蘇省常州市金壇區華城實驗小學 213200）