安徽省滁州中學(239000) 郭守靜 張曉建

多維思考引領教學 生態互動激活課堂
——以一道高考試題的教學運用為例

安徽省滁州中學(239000) 郭守靜 張曉建

2016年4月,筆者所在滁州市郭守靜中學數學名師工作室開展了高三數學復習課中生態課堂的構建研討會,并上了一節關于數列的專題復習課.本節課的設計理念與想法是“多維思考引領教學,生態互動激活課堂”.在設計過程中,筆者以2014年安徽省高考數學理科試題第21題為教學內容,引導學生“多維思考”,開展“生態互動”的教學活動.

真題再現(2014年安徽省高考數學理科第21題)設實數c＞0,整數p＞1,n∈N?.

(1)證明:當x＞?1且x/=0時,(1+x)p＞1+px;

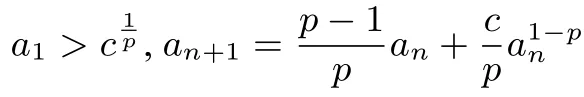
本題的第一小問實際上選自《普通高中課程標準實驗教科書數學選修4-5不等式選講》第四章第二節《用數學歸納法證明不等式》的例3,也即貝努利不等式.高考試題的命制來源于課本的例題,這也要求我們在高三復習中應回歸課本,逐本朔源.在教學過程中,我設計了問題串,促進學生學會合乎邏輯的思考,促使學生自然生成解題思路,多維度的分析問題,達到生態互動,激活課堂.

問題1 此不等式的證明如果把p看作變量,那么就是一個關于正整數的不等式,你能想到用什么方法證明呢?我們常用什么方法證明關于正整數的不等式呢?

學生1 數學歸納法,并順利完成證明.

解法1 (數學歸納法)

(1)當p=2時,由x/=0得(1+x)2=1+2x+x2＞1+2x,不等式成立

(2)假設當p=k(k≥2)時不等式成立,即有(1+x)k＞1+kx.當p=k+1時,(1+x)k+1=(1+x)(1+x)k＞(1+x)(1+kx)=1+x+kx+kx2＞1+(k+1)x所以當p=k+1時不等式成立.由(1)(2)可知,不等式成立.

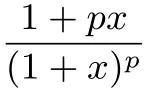
問題3 問題即轉化為證明an＜1,那我們需要解決數列{an}什么方面的性質呢?學生經過思考得到需要研究{an}的單調性,由學生完成并展示解法2.

評析: 此處的設計目的和意圖是通過問題驅動帶動學生去復習鞏固知識,通過解決數列與不等式的基本方法數學歸納法和數列的單調性來解決問題,起到復習基本知識和基本技能的作用.

問題4 我們用數列的思想解決了本題,那么現在我們觀察發現(1+x)p(p＞1,p∈N?),這樣的結構我們同學能夠想到你所學過的什么知識呢?

學生2:二項式定理

教師: 我們可不可以用二項式定理來證明這個不等式呢?由二項式定理可得:(1+x)p=1+px+C2px2+···+Cppxp.

教師:是否可以直接得到(1+x)p=1+px+C2px2+ ···+Cppxp＞1+px?

學生3: 不行,因為x的范圍有影響,可以考慮對分x＞0和?1＜x＜0兩種情況討論.學生考慮的非常好,由此給出下列解法.

解法3:當x＞0時,用二項式定理來證明(1+x)p= 1+px+C2px2+···+xp＞1+px.

教師:當?1＜x＜0時,怎么辦?

學生3:好像不能判斷符號,要不也用數學歸納法證明? (學生發現了問題,但沒有找到解決的辦法,于是又借助前面所學習的方法來解決這種情況)

問題5 當?1＜x＜0,我們是可以用數學歸納法來補充證明,除了數學歸納法之外還有沒有其他的辦法?我們是把p看作變量,來解決問題的,是否可以把x看作變量來研究呢?如果把看作變量,則是一道函數與不等式的問題,我們用什么方法?(這里引導學生突破思維的障礙,變換角度,試圖通過函數與導數的思想方法來解決本題)

學生4:導數

教師: 很好,那同學們思考一下,應該構造怎么樣的函數呢?

學生4:解法4:構造函數,記f(x)=(1+x)p?px?1(x＞ ?1),則f′(x)=p(1+x)p-1?p(x＞ ?1)結合導數可得函數f(x)在(?1,0)上單減,在(0,+∞)上單增故f(x)在x=0處取得極小值即最小值f(0)=0,所以f(x)=(1+x)p?px?1≥0.又x＞?1且x/=0所以f(x)=(1+x)p?px?1＞0,原不等式成立.

學生3:解法3中,當?1＜x＜0時,也可以用導數解決.

評析: 此處的設計目的和意圖是引導學生變換思考的角度,轉變變量,運用函數的思想來解決關于數列和不等式的問題,我們需要借助導數研究函數的單調性,求出最值,進而證明不等式.

教師:非常好,同學們已經從數列的角度以及函數與導數的角度解決的問題,老師在這里還有其他的方法,同學們想不想知道?(學生很是驚奇,還有方法?)

現在我回歸本身,第一問實際上也是一個不等式證明,那我們可不可以用不等式的方法來解決問題呢?

給出引理1:xn?yn=(x?y)[xn-1+xn-2y+···+ xyn-2+yn-1]

教師:同學們可不可以結合上述等式對問題進行分解? (學生都躍躍欲試)

學生5:由xn?yn=(x?y)[xn-1+xn-2y+···+ xyn-2+yn-1],∴(1+x)p?1p=x[(1+x)p-1+(1+x)p-2+ ···+1]

教師:很好,請同學完成解答.

解法5結合xn?yn=(x?y)[xn-1+xn-2y+···+ xyn-2+yn-1]∴(1+x)p?1p=x[(1+x)p-1+(1+x)p-2+ ···+1].

當 x＞ 0時,(1+x)k≥ 1(k=0,1,···,p?1)∴x[(1+x)p-1+(1+x)p-2+···+1]＞px(p≥2)∴(1+x)p?1＞px=?(1+x)p＞1+px.

當?1＜x＜0時有0＜(1+x)k＜1,∴(1+x)p-1+ (1+x)p-2+···+1＜p,∴x[(1+x)p-1+(1+x)p-2+···+1]＞px=?(1+x)p＞1+px.

教師: 我還有個方法,大家想不想知道?(此時的課堂,學生已經完全投入到思考問題,解決問題中,按照我所設計的問題串,學生思維活躍,積極思考)教師給出證明方法:

評析:不等式的解決方法技巧性較強,教師在這里不是讓學生直接去用,二是給出引理,引導學生去試圖解決問題,在提醒的同時,也調動了學生學習的積極性,在引導學生使用什么方法來解決問題的前提下,可以克服學生做題的盲目性.但由于技巧性太強,且超越了考試大綱,故在課堂教學中,教師最終展示了解答.

多維思考引領教學,不僅能是學習者學會學習,促進學生思維的多元化發展,同時也為學習者學會終身學習打下了夯實的基礎.而以生態互動激活課堂的真實意義在于讓學生不再把學習看作是一件痛苦的事情,他們是課堂的主人,他們享受著學習所帶來的快樂,并同時樂于和別人去分享所學,在活動中學習,在問題中學習,透過問題,感悟數學的真諦.

有效就看問題是否發展了學生的數學概括能力,案例2和案例1最大的區別在于學生根據自己的經歷,初步而又基本準確的給出偶函數的定義,也就是抽象出了數學概念,當數學概念被學生準確抽象并合理表達出來后,學生就能更好地理解概念、命題、方法和體系,就能通過概念去認識、理解、把握事物的數學本質,而這時“數學抽象”素養在“概念教學”中就自然而然的“落地生根”了,數學概括的過程也就是數學能力、數學素養的形成過程,這不僅體現在《函數的奇偶性》的概念教學.