計數原理與古典概率復習要點例析*

● 吳寅靜

(余杭區教育局教研室 浙江杭州 311100)

計數原理與古典概率復習要點例析*

● 吳寅靜

(余杭區教育局教研室 浙江杭州 311100)

文章對2017年數學高考中計數原理與概率的復習從知識、能力要求進行說明，并對每一個考點的主要考查方向以典型例題解讀的方式進行分析.

計數原理;概率;二項式定理

1 知識內容

本單元的主要內容有：分類加法計數原理和分步乘法計數原理、排列與組合、二項式定理、楊輝三角與二項式定理.而古典概率主要內容有：事件、事件的關系與運算，互斥、對立、獨立事件，概率與頻率，古典概型.還有離散型隨機變量及隨機變量的分布列、均值、方差，獨立重復試驗的模型及二項分布.2 命題分析

計數原理、概率的內容在這幾年浙江省的數學高考中變化很頻繁，2014年之前是高考的必考內容，2015年、2016年則出現在自選模塊中，2017年開始又進入高考的考試范圍，考試的內容和難度也隨著要求的變化而變化.根據2017年高考考試說明對這一部分內容的要求來看，這些內容在難度上屬于適中，考試題型也以選擇、填空題出現的可能性比較大.

從知識要求看，計數原理與概率的考查最多的是了解層次的內容，要求達到理解層次的主要是分類加法計數原理與分步乘法計數原理及二項式系數的性質，會用排列數公式、組合數公式解決簡單的實際問題，會計算古典概型中事件的概率.

從能力要求看,高考中數據處理能力主要是通過排列、組合、概率與統計來實施的.關鍵是考生能對數據和隨機數據進行提煉得出數據特征，同時考查考生能對眾多數據進行合理篩選、選擇模型、綜合分析數據的思維能力.這對考生的模型建構、思維層次等也提出了較高要求.

3 典例剖析

3.1 計數原理重基礎

很多考生一想到計數原理就是如何用排列組合公式計算出結果，對于分類加法計數原理和分步乘法計數原理則不夠重視.從高考的考試要求來看，2個計數原理是概率的基礎，也是考查邏輯思維能力、分類討論思想、分析解決實際問題的基礎，因此實際問題解決的起點要從2個計數原理開始，而不是直接從排列組合開始思考.

例1 1)在8張獎券中有一、二、三等獎各1張，其余5張無獎.將這8張獎券分配給4個人，每人2張，不同的獲獎情況有______種(用數字作答).

(2014年浙江省數學高考理科試題第14題)

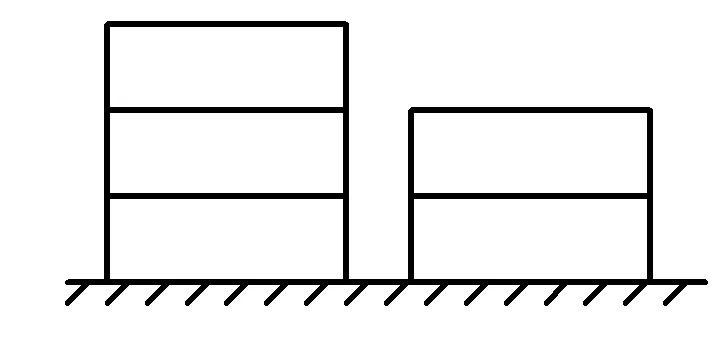
圖1

2)如圖1所示，某貨場有2堆集裝箱，一堆2個，一堆3個，現需要全部裝運，每次只能從其中一堆取最上面的一個集裝箱，則在裝運的過程中不同取法的種數是______(用數字作答).

(2017年浙江省數學高考模擬卷第15題)

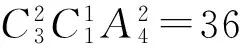
2)將5個集裝箱標上不同的數字或字母，按第1個取的情況分類，再分別用枚舉法即可得共10種.

評注 對計數原理的考查越來越回歸本源，2個計數原理是解決排列與組合問題的基礎，學會辨別分類還是分步，先分類還是先分步都是解決此類問題的關鍵.因此在針對這一內容的復習時重心要適當前移，避免發生重復和遺漏計算、用錯公式的情況.

3.2 概率問題重熱點

高考改革之后，對概率的考查范圍逐漸縮小，但也越來越聚焦在古典概型上.古典概型問題既能考查考生對概率概念的理解程度，同時也能將計數原理中相關的知識進行綜合，因此也成為概率內容命題的熱點.

例2 1)有20張卡片，每張卡片上分別有2個連續的自然數k，k+1,其中k=0,1,2,…,19.從這20張卡片中任取1張，記事件“該卡片上2個數的個位數字之和(例如：若取到標有9，10的卡片，則卡片上2個數的各位數字之和為9+1+0=10)不小于14”為A，則P(A)=______.

2)有5本不同的書，其中語文書2本、數學書2本、物理書1本，若將其隨機地擺放在書架的同一層上，則同一個科目的書都不相鄰的概率是

( )

(2011年浙江省數學高考理科試題第9題)

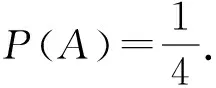
方法1 如何進行分類是解決這個問題的關鍵，其分類依據是從第1本書開始，這個方式雖然比較常規但也是解決實際問題中最為普遍的方式：

①若第1本書是語文書(或數學書)，第2本是數學書(或語文書)，則有4×2×2×2×1=32種可能；

②若第1本是語文書(或數學書)，第2本是物理書，則有4×1×2×1×1=8種可能；

③若第1本是物理書，則有1×4×2×1×1=8種可能.

方法3 對立面的方式不唯一，進行排除的同時一定要關注重復計算的情況：

評注 概率試題的核心是古典概型，古典概型的概率問題常常會與排列、組合融合在一起，而解決排列、組合問題的關鍵是理清完成該動作是分類還是分步.

3.3 二項式定理重關鍵

二項式定理因其內容的原因其考查難度一直不大，最為常見的考查方向就是與二項式系數、二項展開式系數相關的問題，解決這類問題的關鍵就是通項公式.

(2011年浙江省數學高考理科試題第13題)

2)若將函數f(x)=x5表示為f(x)=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5，其中a0,a1,a2,…,a5為實數，則a3=______.

(2012年浙江省數學高考理科試題第14題)

分析 1)此題關鍵是弄清相關項的系數，通項公式在這里起到關鍵作用，即

從而

因為B=4A,所以

解得a2=4.又因為a>0,所以a=2.

2)解法1 此題的最高次數只有5，因此直接用通項公式提出關鍵項的系數，再進行對應系數相等的方式計算，即

解得

a3=10.

解法2 對f(x)=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5的2邊連續對x求導3次，得

60x2=6a3+24a4(1+x)+60a5(1+x)2，

再運用賦值法，令x=-1得60=6a3，即a3=10.此方法不常用，但也是一種拓寬解題思路的方式.

解法3 通過對原函數形式的重新構造，轉化成

f(x)=x5=(1+x-1)5=

(1+x)5-5(1+x)4+10(1+x)3-

10(1+x)2+5(1+x)-1,

從而直接得出a3=10.

評注 二項展開式中二項式系數、項的系數、常數項、有理項等歸根結底就是二項展開式的通項公式.利用二項展開式的通項公式解決這類問題是關鍵，必須熟練掌握.同時二項式中對整個式子結構的重構、變形也是考查考生思維靈活性的一個方向，也需要在平時的復習中加以訓練.

3.4 離散型隨機變量及其分布列重應用

離散型隨機變量及其分布列在2015年、2016年浙江省數學高考試題和自選模塊中都沒有作為考試內容，在2017年的高考考試說明中也基本以了解為主，這一塊內容的復習以掌握基本概念、基本技能為重點，學會從相對簡單的實際問題中提煉出問題模型并加以解決.

例4 1)隨機變量ξ的分布列如表1所示：

表1 隨機變量ξ的分布列

(2017年浙江省《數學高考考試說明》題型示例)

2)已知箱中裝有4個白球和5個黑球，且規定：取出一個白球得2分，取出一個黑球得1分.現從該箱中任取(無放回，且每球取到的機會均等)3個球，記隨機變量X為取出此3球所得分數之和；

①求X的分布列；

②求X的數學期望E(X).

(2012年浙江省數學高考理科試題第19題)

分析 1)出現2個變量即需要建立方程組，即

2)先確定X的可能取值有3，4，5，6，然后根據實際情況計算每一種情況的概率

由此可得X的分布并計算出數學期望

評注 離散型隨機變量及其分布列從現有的情況來看,考查難度不會太大，但由于其具有一定的綜合性和應用性，學生在理解隨機變量X的取值及其概率計算時常常會出錯，因此平時在這方面的復習還需關注.

4 精題集萃

1.將2個相同的白球、3個相同的紅球、4個相同的黑球全部投入A,B,C這3個袋中，則無空袋的投放方法有

( )A.723種 B.865種 C.900種 D.1 204種

( )

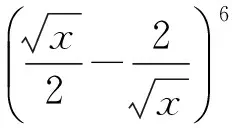
3.甲、乙、丙3人各寫一張賀卡隨意送給丁、戊2人中的一人，則丁、戊2人中恰有一人收到一張賀卡的概率是

( )

4.將5個大小互不相同的球放入編號為1，2的2個盒子中，要求每個盒子里放入的球數不小于編號數，則不同的放球方法有______.

5.若(1-2x)2 017=a0+a1x+a2x2+…+

6.一個均勻小正方體的6個面中，3個面上標有數0，2個面上標有數1，1個面上標有數2，將這個小正方形拋擲2次，則向上的數之積的數學期望是______.

8.某市教育局組織中學生足球比賽，共有實力相當的8支代表隊(含有一中代表隊、二中代表隊)參加比賽，比賽規則如下：

第1輪：抽簽分成4組，每組2隊進行比賽，勝隊進入第2輪;第2輪：將4隊分成2組，每組2隊進行比賽，勝隊進入第3輪;第3輪：2隊進入決賽，勝隊獲得冠軍.

現記ξ=0表示整個比賽中一中代表隊與二中代表隊沒有相遇，ξ=i表示恰好在第i輪比賽時一中代表隊與二中代表隊相遇(其中i=1,2,3).

1)求ξ的分布列；

2)求Eξ.

參 考 答 案

8.解 1)ξ可取0，1，2，3,則

表2 隨機變量ξ的分布列

2016-12-31；

2017-02-23

吳寅靜(1974-)，女，浙江杭州人，中學高級教師.研究方向：數學教育.

O122.4

A

1003-6407(2017)04-44-04