高考知識專題：數列與數學歸納法*

●嚴興光 李紹塔

(杭州第十四中學 浙江杭州 310000)

高考知識專題：數列與數學歸納法*

●嚴興光 李紹塔

(杭州第十四中學 浙江杭州 310000)

數列是近幾年浙江省數學高考的重點也是難點之一.文章從近幾年高考卷對數列的考查情況入手，由淺入深分析高考中數列題所考查的內容、常用的解題方法、壓軸題的出題方向、解壓軸題常用的數學思想方法以及如何突破數列壓軸題等.

數列；數學歸納法；不等式

1 知識內容

數列部分主要內容有：等差(等比)數列,數列求通項的基本方法，數列求和的基本方法，比如疊加法、疊乘法、倒序相加法、錯位相減法、裂項法等，以及不等式與數列的綜合問題和利用數學歸納法證明數列問題等．

2 命題分析

從考查形式看，在歷年的浙江省數學高考中，數列問題一般以1個小題(填空題或選擇題)和1道解答題的形式出現.作為考查考生創新意識與實踐精神的最好素材，一些構思精巧、新穎別致、極富思考性和挑戰性的數列與方程、函數、不等式等的綜合性試題不斷涌現，這部分試題往往以壓軸題的形式出現，考查綜合運用知識的能力，突出知識的融會貫通．

從考查內容看，小題主要以等差數列和等比數列為載體，考查數列的概念、表示法、求通項、求和等；綜合題常與不等式、函數的最值、歸納猜想、分類討論等數學思想相結合，技巧性比較強，需要平時一定量的訓練與積累，在后續復習時應予以關注．

3 典題剖析

考點1 數列求通項問題

與通項公式有關的問題是前幾年浙江省數學高考數列小題考查的重點內容，主要知識點有：等差(等比)數列通項公式、一些簡單的可以轉換為等差數列或等比數列的遞推式以及周期數列等．

例1 設等比數列{an}滿足a1+a3=10，a2+a4=5，則a1a2…an的最大值為______.

于是當n=3或n=4時，a1a2…an取到最大值26=64．

例2 設數列{an}的前n項和為Sn，數列{Sn}的前n項和為Tn，滿足Tn=2Sn-n2，其中n∈N*.

1)求a1的值；

2)求數列{an}的通項公式．

考點2 數列求和問題

數列求和的常用方法有公式法(等差數列和等比數列)、倒序相加法、錯位相減法、裂項相消法、分組轉化求和法、并項求和法，在解題過程中要合理選擇求和公式．

1)求數列{an}，{bn}的通項公式；

評注 利用裂項相消法求和時，應注意：1)抵消后并不一定只剩下第1項和最后1項，也有可能前面剩2項，后面也剩2項；2)將通項公式裂項后，有時候需要調整前面的系數，使裂開的2項之差和系數之積與原通項公式相等．

考點3 數列綜合問題

數列解答題一般具有很強的綜合性，考查的知識以等差、等比數列的性質為主，兼顧其他知識．

數學歸納法是一種證明與正整數n有關的數學命題的重要方法．

1)證明：an+1>an；

證法2 用數學歸納法證明an+1>an>2.

由歸納假設可得ak+2>ak+1>2 成立.

綜上所述，an+1>an成立.

進而

由

知

評注 裂項求和是求解本題的關鍵.由于本題涉及的裂項方法不常規，復習過程中特別要引起重視.類似的問題還有2015年浙江省高中數學競賽試題第6題：

( )

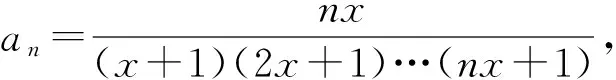
分析 由題意

即

(x+1)(2x+1)…(2 015x+1)>0，

于是

考點4 數列與不等式綜合問題

數列是特殊的函數，不等式是深刻認識函數與數列的重要工具，2者的綜合是近幾年高考命題的新熱點，且數列的重心已經偏移到不等式的證明與求解中，而不再是以前的遞推求通項．

例6 已知數列{an}滿足a1=1，an+1=3an+1.

3n-1≥2·3n-1，

從而

于是

故

評注 對于數列問題中求和類不等式的證明，若是通過放縮的方法進行證明的，則一般有2種類型：1)能夠直接求和(或求積)，再放縮；2)不能直接求和(或求積)，需要放縮后才能求和(或求積)，求和(或求積)后再進行放縮(比如本題)，一定要注意“縮的尺度”和“從哪一項開始放縮”．

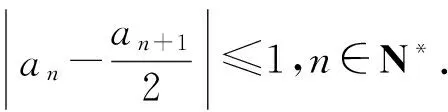
1)證明：|an|≥2n-1(|a1|-2),n∈N*；

本題作為浙江卷2016年高考試題，體現浙江高考試題入口寬、方法多、結構精巧、簡約而不簡單的特點．

即

對右邊的不等式2邊同除以2n,得

從而當n≥2,n∈N*時，

故

|an|≥2n-1(|a1|-2),

另外，當n=1時，顯然成立.綜上，|an|≥2n-1(|a1|-2),n∈N*.

因此，將這些知識和方法遷移至本題的證明如下：

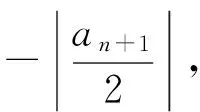
|an+1|+2≤2(|an|+2)，

從而

|an|+2≤2n-1(|a1|+2)，

即 |an|≤2n-1(|a1|+2)-2,

(1)

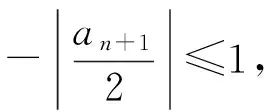
|an+1|-2≥2(|an|-2)，

若|an|>2，則易得

|an|-2≥2n-1(|a1|-2),

即 |an|≥2n-1(|a1|-2)+2,

(2)

如果(2)式成立，那么第(1)問所證結論|an|≥2n-1(|a1|-2)成立.

這里，為得到(2)式，添加|an|>2這個條件，下面來說明這個條件的合理性.

①當|a1|≤2時，則|an|≥0≥2n-1(|a1|-2)顯然成立；

②當|a1|>2時，則由|an+1|-2≥2(|an|-2)，再結合數學歸納法的思想，易得|an|>2，從而|an|≥2n-1(|a1|-2)+2>2n-1(|a1|-2)成立．

2)證法1 延續第(1)問證法1的思想，則任意n，m∈N*,m>n,有

故

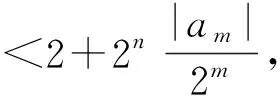
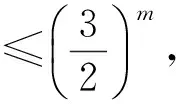
再由m的任意性可得|an|≤2,n∈N*，理由如下：

綜上，任意n∈N*,|an|≤2.

假設任意n∈N*,|an|≤2不成立，即存在k∈N*,|ak|>2成立.則由第(1)問證法2同理可得

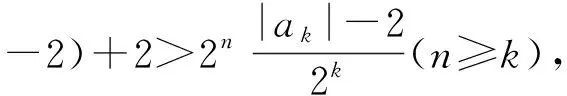
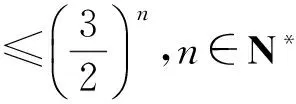
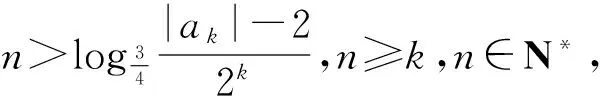
即

因此，假設不成立，從而任意n∈N*,|an|≤2.

評析 第1)小題所證的式子|an|≥2n-1(|a1|-2)中已經在提示考生，需要進行|an|-2的代數變形，然后放縮出一個等比數列，這也正是浙江省高考一直以來的特點，難題總是會留下一些線索，讓考生“有機可乘”．

m·2n≤2n-1(|a1|-2)+2≤|an|≤2n-1(|a1|+2)-2≤M·2n(其中m>0,M>0).

4 精題集萃

1．已知等差數列{an}前9項的和為27，a10=8，則a100=

( )

A.100 B.99 C.98 D.97

2．設{an}是等差數列，下列結論中正確的是

( )

A．若a1+a2>0，則a2+a3>0 B．若a1+a3<0，則a1+a2<0

3．已知{an}為等差數列，Sn為其前n項和，若a1=6，a3+a5=0，則S6=______.

4．設Sn是數列{an}的前n項和，且a1=-1，an+1=SnSn+1，則Sn=______．

5．無窮數列{an}由k個不同的數組成，Sn為{an}的前n項和.若對任意n∈N*，Sn∈{2,3}，則k的最大值為______.

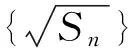
7．設等差數列{an}的公差為d，前n項和為Sn，等比數列{bn}的公比為q．已知b1=a1，b2=2，q=d，S10=100．

1)求數列{an}，{bn}的通項公式；

圖1

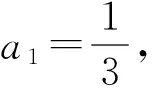
參 考 答 案

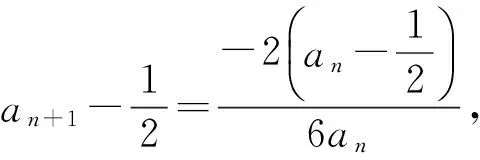
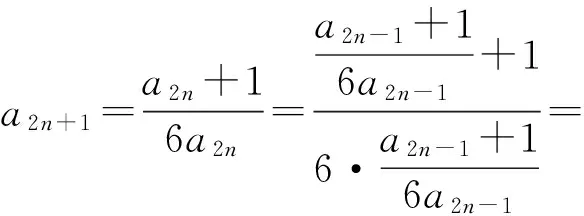
2017-01-04；

2017-02-23

嚴興光(1975-)，男，浙江杭州人，中學高級教師.研究方向：數學教育、技術與數學課程整合研究.

O122

A

1003-6407(2017)04-29-05