文理合卷后2017年浙江省數學高考測試卷分析暨2017年高考展望*
●高雄略 吳文廣
(永康市第一中學 浙江永康 321300)
文理合卷后2017年浙江省數學高考測試卷分析暨2017年高考展望*
●高雄略 吳文廣
(永康市第一中學 浙江永康 321300)
文章站在命題人角度通過對2017年浙江省數學高考測試卷的試卷結構、考點分布及試題構造、解法策略等方面進行研究,并對比分析歷年浙江省數學高考試題,展望新高考改革后的2017年浙江省數學高考,同時提出若干數學復習建議.
測試卷;浙江高考;展望
浙江省數學高考文理分卷已有30多年的歷史,如今文理合卷的考試改革令全省高中數學教師和廣大學生甚為關切,但頗感迷茫.隨著《2017年浙江省普通高考考試說明——數學》的發布,全省的師生漸漸有了方向,特別是省測試卷的出現,更是猶如春暖花開.省測試卷既是命題者對學情的一種調研,也是各校教師和學生對考情把握的重要窗口,那么它會對數學復習備考帶來怎樣的意義呢?懷揣著這樣的問題,筆者試著在考試說明解讀的基礎上對測試卷作一番分析,希望能從中有所收獲,并給下一階段復習帶來一些啟示.
1 2017年數學高考測試卷分析
1.1 穩中有變,文理交融
1)試卷把握“起點低,坡度緩,層次多,區分好”的命題策略,編排呈現文科直觀形象思維和理科抽象理性思維的有機結合,體現“文頭理尾,文理交融”的特點.
2)重基礎,重綜合,重本質,重方法,突出能力立意.試卷敘述簡約而不失厚重,試題本質清晰,背景深刻,但講究方法靈活,策略得當.
3)試卷結構、形式以及考點穩中有變.選擇題由“8×5”變成“10×4”,填空題、解答題穩定.新增考點的考查難度較以往降低,如復數、空間向量、排列組合、概率與統計、導數等.三角函數、函數與導數的大題和以往文科函數題要求相當,特別是有關導數的應用,降低了分類討論的難度.立體幾何大題與以往文科考線面角難度一致,方法上側重綜合法,降低空間向量的應用難度.解析幾何主要側重對直線、圓、橢圓與拋物線的考查,對雙曲線的要求明顯降低,大題考查直線與橢圓,難度與以往理科試題難度相當.數列與不等式綜合壓軸題綜合程度高,設問起點低、中間活、收尾難.
1.2 問題驅動,理性嚴謹
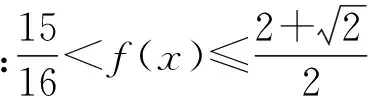
( )
A.a·(b+c)=0 B.a·(b-c)=0C.(a+b)·c=0 D.(a-b)·c=0
方法1 設a·c=x,b·c=y,則由
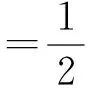
2|x|=2|y|=|y+x|(其中x,y∈R)
顯然x=y.
( )A.F(-a)≥F(a)且F(1+a)≥F(1-a)B.F(-a)≥F(a)且F(1+a)≤F(1-a)C.F(-a)≤F(a)且F(1+a)≥F(1-a)D.F(-a)≤F(a)且F(1+a)≤F(1-a)方法1 取f(x)=g(x)=x2,則
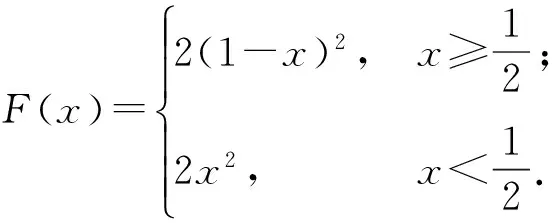
F(x)=2min{f(x),g(1-x)},則
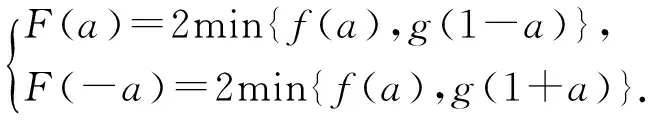
1+a>|1-a|,即
g(1+a)>g(1-a),故F(a)≤F(-a),同理可得
F(1+a)≥F(1-a).
點評 選擇題的求解,只有靈活運用方法,方能進退有據,不失方寸,可謂小題小做之道.題17 已知函數f(x)=x2+ax+b(其中a,b∈R)在區間(0,1)上有2個零點,則3a+b的取值范圍是______.
方法1 直接探索系數a,b的約束條件
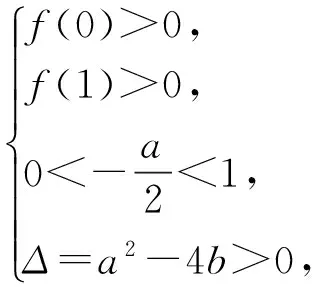
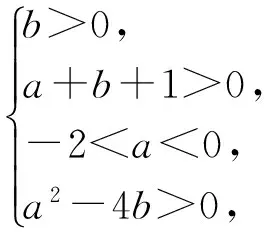
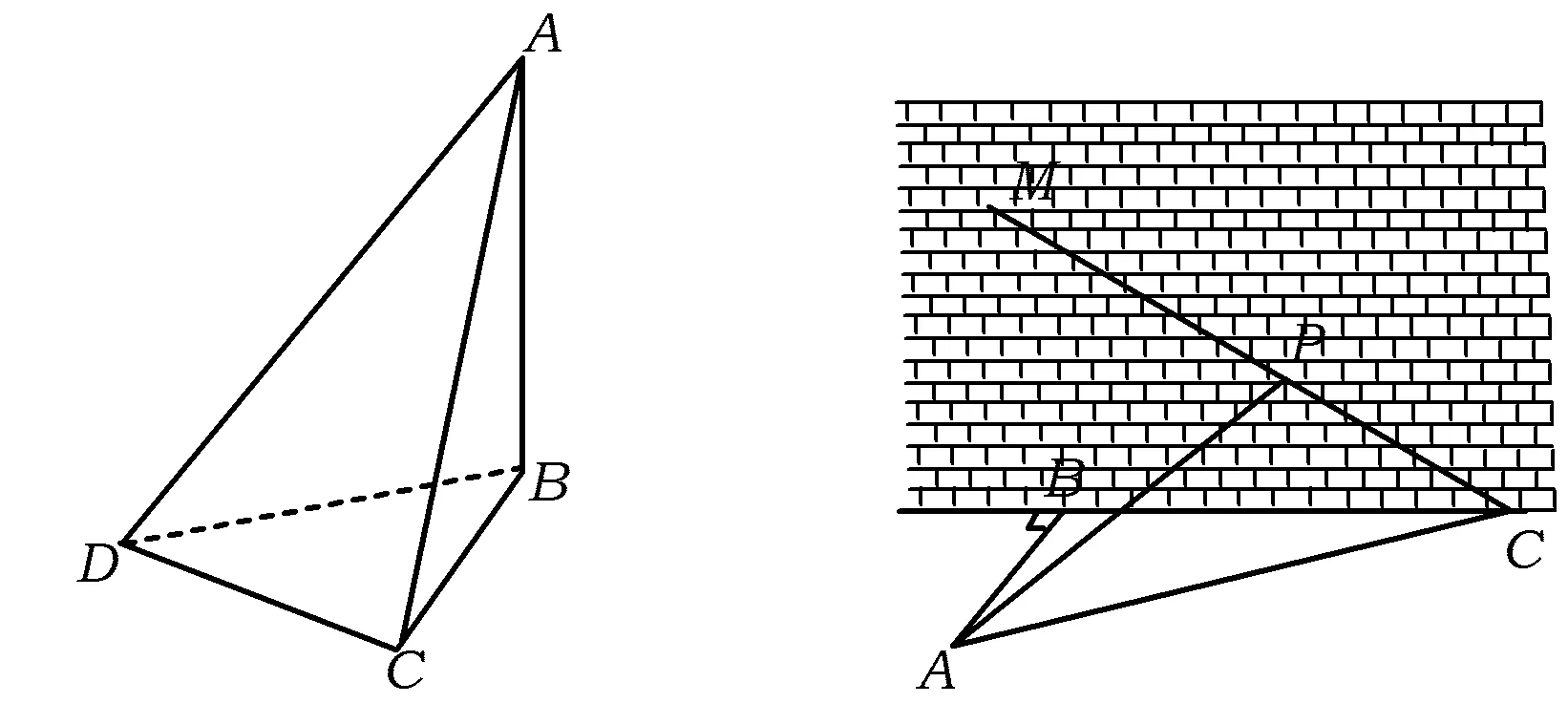
可用規劃的方法求解3a+b的取值范圍.方法2 將問題化歸為“已知函數f(x)=(x-s)(x-t),其中0 點評 將問題進行合理的等價轉化與化歸,是探索解題的重要思想方法,是數學思維的重要方式,是認識該題本質的重要途徑. .1)證明:OP⊥BC; 1)證法1 設直線PA的方程為 kBC·kOP=-1,于是 整理得(t-1)(5t2+2t+12)=0.因為5t2+2t+12>0,所以t=1. 點評 2種方法分別以直線與橢圓、點與橢圓的位置關系著手考慮問題,但其考查解析法的核心未變,運算能力的要求較高.解題者不僅要明算理,更要會執行,最后才能“撥開迷霧見青天”,一覽無余. 1.4 立足本質,常考常新測試卷中很多試題與其說是測試,不如說是對前幾年高考命題思路的一種展示(可能本身就是高考題的備選題,或者磨題過程中的過程題),這為我們研究、了解高考的命題提供了一個非常重要的窗口.下面就選取幾道題與高考真題作對比分析,且看其如何立足本質,常考常新. 1)第9題:意在考查“平面內任一直線與另一平面所成的線面角不大于2個平面的二面角的大小”,結論證明如下: 如圖1所示的四面體A-BCD中,AB⊥平面BCD,CD⊥平面ABC,易得∠ACB即為二面角A-CD-B的平面角,∠ADB即為直線AD與平面BCD所成的線面角.因為在Rt△BCD中,BD>BC,所以 ∠ADB<∠ACB. 圖1 圖2 點評 該題仰角θ即為平面AMC中的動直線與水平地面的所成角,其最大值等于二面角M-AC-B的大小. 復習中以不妨將勾股四面體即“四面都是直角三角形的四面體”作為研究對象,開展教學活動來探索其性質及簡單應用,同時培養學生的基本活動經驗,并通過概括積累一些重要的結論. 1)夯實雙基,注重通性通法,授課以講授與活動課相結合,加強學生基本活動經驗的積累,并概括總結,在此過程中滲透數學思想,提升數學思維的張力和自主思考、探索解題的能力. 2)回歸教材,并高于教材,復習課充分利用教材中的例題、習題、閱讀材料等[1],通過變式教學,舉一反三,突破核心,深刻挖掘其教學功能,幫助學生構建數學知識體系. 3)重視專題的探索教學,關注歷年高考的命題重點、熱點,尋找生長點.同時不斷地概括總結,還原數學本質,領會數學思想,形成嚴謹、深刻的數學思維素養. 4)高三教師應多參與交流研討,及時掌握高考動態,并不斷進行自我學習,加強自身對學科和教學的雙重理解.學生的成長是教師的歸宿,只有教師本身站得高,學生才能走得遠.德國數學家克萊因在給中學教師做講座時說:“一個數學教師的職責是應使學生了解數學并不是孤立的各門學問,而是一個有機的整體,基礎數學的教師應該站在更高的視角(高等數學)來審視.理解初等數學問題,只有觀點高了,事物才能顯得明了而簡單;一個稱職的教師應當掌握或了解數學的各種概念、方法及其發展與完善的過程以及數學教育演化的經過.”[2] [1] 徐世白.2013年浙江省《考試說明》樣卷與高考真題對比分析暨2014年高考展望[J].中學教研(數學),2014(5):34-37. [2] 克萊因.高觀點下的初等數學[M].上海:復旦大學出版社,2008. 2016-12-21; 2017-02-16 高雄略(1983-),男,浙江永康人,中學一級教師.研究方向:數學教育. O12 A 1003-6407(2017)04-26-04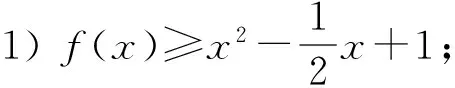
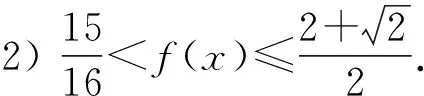
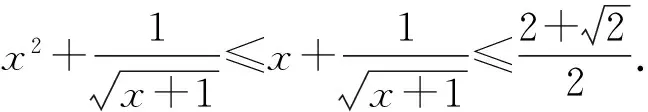
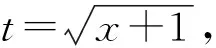


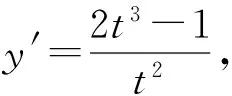
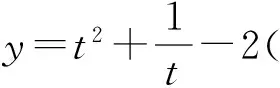


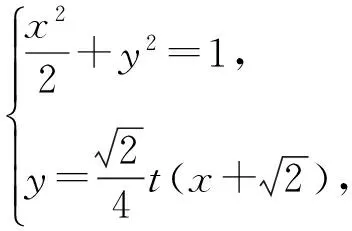
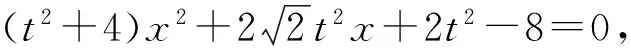
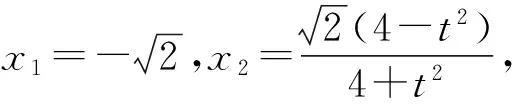

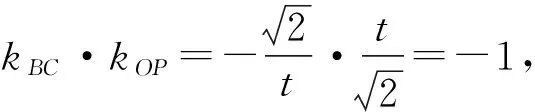
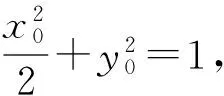
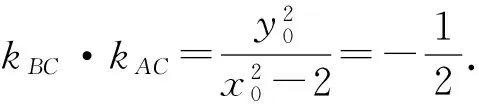
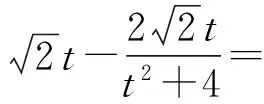



2 2017年浙江省數學高考復習建議

