從解析法到幾何直觀*
——從幾道與圓有關(guān)的試題談圓的幾何直觀

●李守明

(舟曲中學(xué) 甘肅蘭州 730087)

從解析法到幾何直觀*
——從幾道與圓有關(guān)的試題談圓的幾何直觀

●李守明

(舟曲中學(xué) 甘肅蘭州 730087)

圓具有許多直觀的幾何性質(zhì)，在高中解析幾何中若能合理運(yùn)用這些性質(zhì)，則能夠理解與圓有關(guān)的解析幾何試題產(chǎn)生的幾何背景，并且簡化解析幾何的運(yùn)算.文章從一道高三復(fù)習(xí)試題入手，結(jié)合高考試題，闡述了圓的直觀幾何性質(zhì)在解題中的意義.

圓；解析法；幾何直觀

在高三解析幾何有關(guān)圓的章節(jié)復(fù)習(xí)中，遇到這樣一個試題：

圖1

例1 如圖1所示，⊙C是坐標(biāo)平面上通過點(diǎn)M(0,-2)，N(6,4)的圓，若⊙C與x軸交于點(diǎn)A，B，求線段AB長的最小值.

遇到一個數(shù)學(xué)問題，首先想到解題切入點(diǎn)與思路是什么？其次想到的是有沒有簡便易行的方法？帶著這樣2個想法，筆者走進(jìn)了解題之旅.

1 解題的切入點(diǎn)及思路

這道題是求⊙C與x軸相交的弦AB長的最小值，是一道求最值的問題.只有變化的量才能引起最值，一般應(yīng)該建立起弦AB的長與某個變量的函數(shù)關(guān)系，借助求函數(shù)值域的方法來解決，故本題的關(guān)鍵是如何表示出弦AB的長.從解析幾何中如何求直線與圓相交弦長入手，因此有了如下思路：

思路1 在⊙C中，借助垂徑定理，構(gòu)造直角三角形來求弦長.

解法1 設(shè)⊙C的標(biāo)準(zhǔn)方程為

(x-a)2+(y-b)2=r2，

則

又M(0,-2)，N(6,4)在⊙C上，從而

消去r2，得到

a+b=4，

因此AB2= 4(r2-b2)=

4[(6-a)2+(4-b)2-b2]=

4[(6-a)2+a2-(4-a)2]=

4[(a-2)2+16]≥64，

當(dāng)a=2時，取到等號,故線段AB長的最小值為8.

思路2 線段AB是x軸與⊙C的交點(diǎn)弦，故可以通過弦長公式來表示弦長.

解法2 設(shè)⊙C的一般方程為

x2+y2+dx+ey+f=0，

由M(0,-2),N(6,4)在⊙C上，得

消去d和f，得到

x2+y2-(8+e)x+ey+2e-4=0.

設(shè)A(x1,0)，B(x2,0)，則

x1+x2=8+e，x1x2=2e-4，

從而AB2= |x1-x2|2=(x1+x2)2-4x1x2=

(e+4)2+64≥64，

當(dāng)e=-4時,取到等號，滿足d2+e2-4f>0,故線段AB長的最小值為8.

思路3 線段AB所在直線為x軸，經(jīng)過定點(diǎn)P，傾斜角為0°，故可以設(shè)出直線的參數(shù)方程，利用參數(shù)的幾何意義表示線段AB的弦長.

解法3 根據(jù)思路2，⊙C的方程為

x2+y2-(8+e)x+ey+2e-4=0.

又依據(jù)兩點(diǎn)式可求出直線MN的方程為

x-y-2=0，

令y=0，則x=2，故P(2,0)，直線AB的參數(shù)方程為

代入x2+y2-(8+e)x+ey+2e-4=0，得

t2-(4+e)t-16=0.

設(shè)點(diǎn)A,B對應(yīng)的參數(shù)分別為t1,t2，則

AB2= |t1-t2|2=(t1+t2)2-4t1t2=

(e+4)2+64≥64,

當(dāng)e=-4時,取到等號，滿足d2+e2-4f>0，故線段AB長的最小值為8.

評注 解題方法的不同是因?yàn)榻忸}思路的不同，這3種思路建立弦長AB與某個變量關(guān)系的角度雖然不同，其實(shí)本質(zhì)是相同的，都是把弦長AB作為函數(shù)，分別建立了與變量a(思路1)和變量e(思路2和思路3)的函數(shù)關(guān)系，最后借助求二次函數(shù)值域的方法得到弦長AB的最小值.思路自然親切，操作性強(qiáng)，學(xué)生易于掌握.

解析幾何是用代數(shù)的方法研究幾何問題，解析幾何求最值的試題中，若題目的條件和結(jié)論能體現(xiàn)一種明確的函數(shù)關(guān)系，則優(yōu)先考慮建立起目標(biāo)函數(shù)，然后求這個函數(shù)的最值，常用配方法、基本不等式法及導(dǎo)數(shù)法等求解.

此題能否從⊙C的幾何性質(zhì)入手，借助幾何直觀來解決這個問題呢？

2 解題的簡便方法：幾何直觀

思路4 由于⊙C只是經(jīng)過點(diǎn)M,N的圓，并不是固定的，⊙C的變化引起了與x軸相交弦AB的變化，但這個弦有個特點(diǎn):經(jīng)過定點(diǎn)P.另外,靜止和運(yùn)動是相對的，我們可以固定⊙C，讓x軸變化，那么這個問題就轉(zhuǎn)化為經(jīng)過圓內(nèi)一定點(diǎn)P的弦長的最小值是多少的問題了，從而有了下面的解法：

解法4 經(jīng)過⊙C內(nèi)定點(diǎn)P的弦AB與CP垂直時弦長最短.此時圓心C在直線x=2與MN垂直平分線的交點(diǎn)處.

MN垂直平分線的方程為x+y-4=0，令x=2，代入x+y-4=0,則y=2，從而C(2,2)，于是

r2=CN2=20.

⊙C的方程為 (x-2)2+(y-2)2=20，

令y=0，x1=-2，x2=6，則

AB=|x1-x2|=8,

故線段AB長的最小值為8.

思路5AB與MN是圓內(nèi)經(jīng)過定點(diǎn)P的2條相交弦，可以充分利用初中學(xué)過的平面幾何知識，利用相交弦定理來解決.

從而

PA·PB=PM·PN=16，

根據(jù)基本不等式

當(dāng)PA=PB=4時,取到等號.

評注 思路4需要明確經(jīng)過圓內(nèi)一點(diǎn)的弦在哪種情況下取得最小值這個條件，這就要求平時的積累和總結(jié)；思路5發(fā)揮了圓自身的幾何性質(zhì)，相交弦定理對高中學(xué)生來說，是圓的一種很直觀的性質(zhì)，與基本不等式相結(jié)合，簡化了解題的程序，確有神來之筆的一種感覺.思路4和思路5都是圓的幾何直觀在解析幾何解題中體現(xiàn)出來的，幾何直觀在解析幾何解題中的顯著作用是解析法不可替代的.

3 圓的幾何直觀的意義

3.1 借助圓的幾何直觀，理解試題的產(chǎn)生背景

( )

(2016年四川省數(shù)學(xué)高考理科試題第10題)

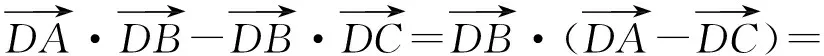
因此點(diǎn)D既是△ABC的外心又是垂心，從而△ABC為等邊三角形.又

故

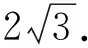
圖2

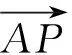
x2+(y-3)2=1.

進(jìn)而

故選B.

思路2 (向量法)如圖2，取AC的中點(diǎn)為E，則

于是

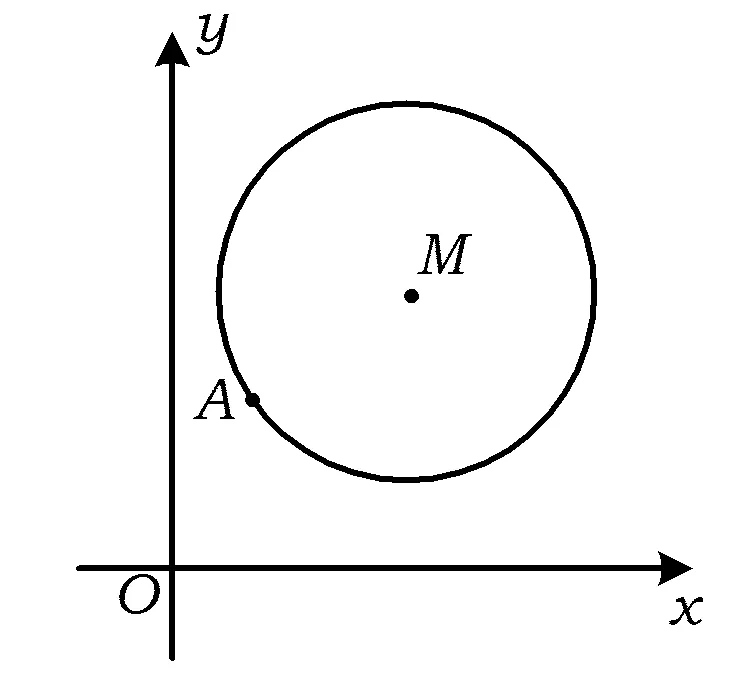
圖3

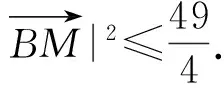
評注 比較以上3種思路，思路3不僅解題方法簡潔，更能反映試題產(chǎn)生的背景：圓外一點(diǎn)與圓上點(diǎn)確定線段長度的最值問題.

3.2 借助圓的幾何直觀，簡化解析幾何運(yùn)算解析幾何的解題過程中，幾何條件的轉(zhuǎn)化對解題的難易起著決定作用，引導(dǎo)學(xué)生從圖形入手，挖掘幾何圖形隱藏的條件，利用幾何直觀解題顯得非常簡單.

例2 如圖3，在平面直角坐標(biāo)系xOy中，已知以M為圓心的⊙M:x2+y2-12x-14y+60=0及其上一點(diǎn)A(2,4).

1)設(shè)⊙N與x軸相切，與⊙M外切，且圓心N在直線x=6上，求⊙N的標(biāo)準(zhǔn)方程；

2)設(shè)平行于OA的直線l與⊙M相交于點(diǎn)B,C，且BC=OA,求直線l的方程；

(2016年江蘇省數(shù)學(xué)高考試題第18題)

1)(x-6)2+(y-1)2=1；

2)l:y=2x+5或y=2x-15.

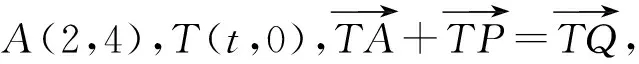
(1)

(1)又因?yàn)辄c(diǎn)Q在⊙M上，所以

將式(1)代入式(2)，得

(x1-t-4)2+(y1-3)2=25

從而

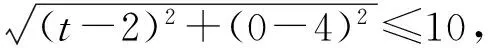
解得

評注 本題第3)小題的解法1從2個圓有公共點(diǎn)這個條件入手，2個圓的圓心距滿足關(guān)系|R-r|≤d≤R+r，建立了關(guān)于t的不等式，思路清楚但略顯繁瑣；而解法2充分利用已知條件，從簡單的幾何直觀可以知道圓上任意2個點(diǎn)的距離不超過直徑的長度這一事實(shí)，以此為依據(jù)建立關(guān)于t的不等式，大大地減少了解析幾何的運(yùn)算量，令人耳目一新！

4 結(jié)束語

我國數(shù)學(xué)教育家徐利治曾說過：“直觀就是借助于經(jīng)驗(yàn)、觀察、測試或類比聯(lián)想，所產(chǎn)生的對事物關(guān)系直接的感知與認(rèn)識，而幾何直觀是借助于見到的或想到的幾何圖形的形象關(guān)系產(chǎn)生對數(shù)量關(guān)系的直接感知.”熟悉幾何圖形的性質(zhì)是幾何直觀感知的源泉，但并不是每道題都有明顯的幾何直觀，在教學(xué)中，教師有意識地培養(yǎng)學(xué)生的幾何直觀能力，對提高學(xué)生思維的深刻性和靈活性一定是大有裨益的.

2016-12-26；

2017-02-20

李守明(1974-)，男，甘肅秦安人，中學(xué)一級教師.研究方向：數(shù)學(xué)教育.

O123.1

A

1003-6407(2017)04-11-03