筒體接管的力學分析

宿 昊，唐興齡（中國核電工程有限公司，北京 100840）

筒體接管的力學分析

宿 昊，唐興齡
（中國核電工程有限公司，北京 100840）

在壓水堆核電設備的強度計算校核中，經常需要對圓筒型容器上的接管進行評估。本研究分別采用有限元殼體單元和實體單元模型以及公式法預估對筒體的接管進行單變量作用下的應力分析。結果表明運用有限元殼體模型得到的結果是保守的，典型載荷下內壓對接管最大應力強度的影響是最為顯著的。公式法預估最大應力強度應在使用厚壁殼體公式基礎上乘以一定的應力集中系數。這些結果將為以后涉及設備接管應力強度的估計及評定提供參考。

筒體接管；應力分析；接管載荷

圓筒型容器是壓水堆核電設備中的常見類型，包括立式、臥式兩種。這些筒體上分布著許多直徑不等的接管與其他設備相連，而且一般來說這些接管相對于筒體本身的直徑都很小，并與筒體正交貫通形成T型結構。由于計算筒體時一般建立的是殼體單元，這些接管也被方便地按殼單元處理，這樣的結果往往是接管部分的應力超出RCC-M規范的限定范圍[1-3]，最終需要再取出局部區域建立實體單元模型來進行應力分析。本文分別運用有限元殼體單元和實體單元方法，并結合理論公式對典型筒體同一個接管的應力情況進行分析和對比，為以后此類評定提供一個良好簡捷的結果預估參考。

1 結構特性

本文研究的核電設備的安全級別為核安全2級。取典型設備尺寸與材料如下：筒體覬300×10mm，即筒體外徑300mm，厚度10mm。外接支管為3/4"管，即截面尺寸為覬26.7×5.54mm，高度為筒體外徑正交向上延伸50mm。各部分材料均取為00Cr19Ni10，設計溫度343℃，在該設計溫度下材料的力學性能參數見表1所示。

表1 材料力學性能參數[1]

2 計算方法

2.1 有限元法

對筒體連接接管結構進行有限元[4]建模，采用殼體單元（SHELL181）和實體單元（SOLID45），整體模型結構如圖1所示。在殼體左右的邊界處施加固定邊界約束，在外部支管的管道口圓心處各建立一點，并與管口面通過MPC技術連接在一起用于施加接管載荷，內壓施加在殼體和接管的內表面并在加載的接管頭處進行載荷補償。

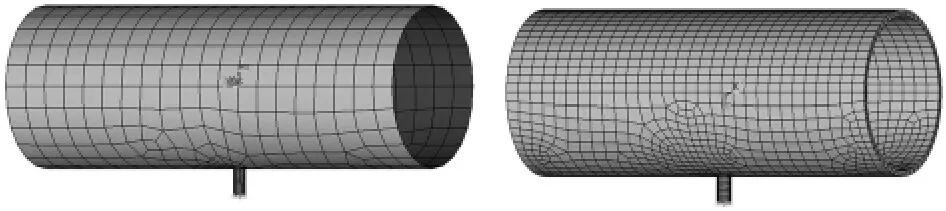
圖1 筒體接管的殼體/實體有限元模型

對于內部壓力和接管載荷，本文分別取各典型分量進行單獨計算，如表2所示。表中，沿接管軸向為Z，沿筒體軸向為Y，X軸垂直于YZ平面，構成右手坐標系。

2.2 公式法

對于內壓作用，將圓筒接管看作為圓筒和接管的組合，即看作兩個正交殼體結構的疊加。由材料力學[5]知識，內壓作用下環向應力大于周向應力，薄壁殼體環向應力公式為：σ=pD/（2t），而厚壁殼體的最大環向應力為σ=p（b2+a2）/（b2-a2）。其中p為壓力，D、t分別為薄壁殼體的直徑和厚度，b、a分別為厚壁殼體的外徑和內徑。

而對于接管載荷中力及力矩的作用，可以將接管簡單看作一端固支另一端加載的梁，此處不再列出相關公式。

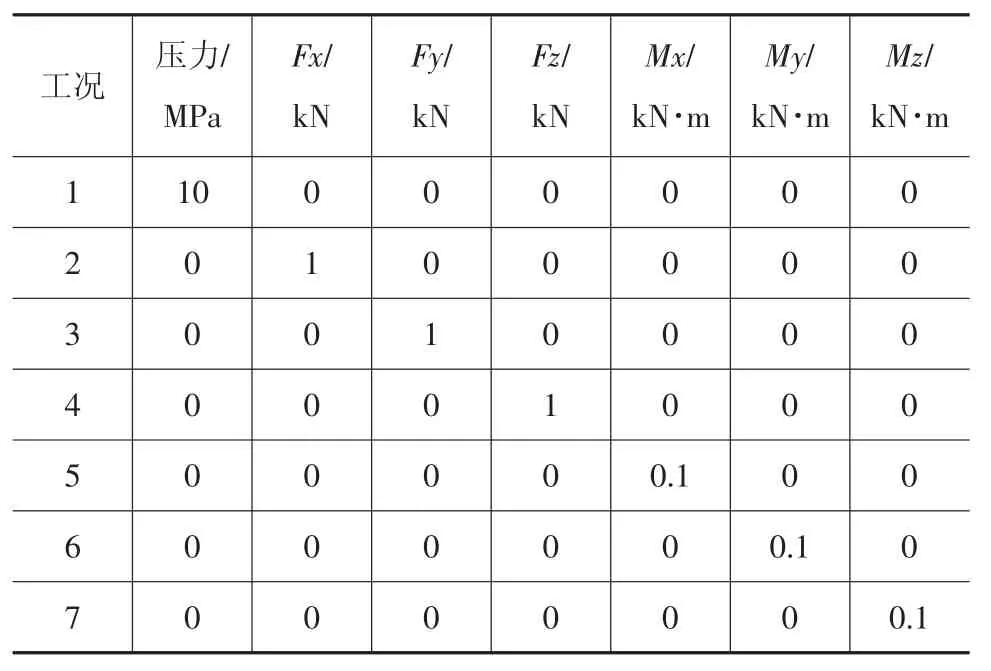
表2 壓力與接管載荷

3 計算結果與討論

3.1 有限元方法

如圖2所示，由計算后的應力強度分布圖可知，設備的最大應力強度出現在接管根部，因此下面的應力分析主要針對接管根部。

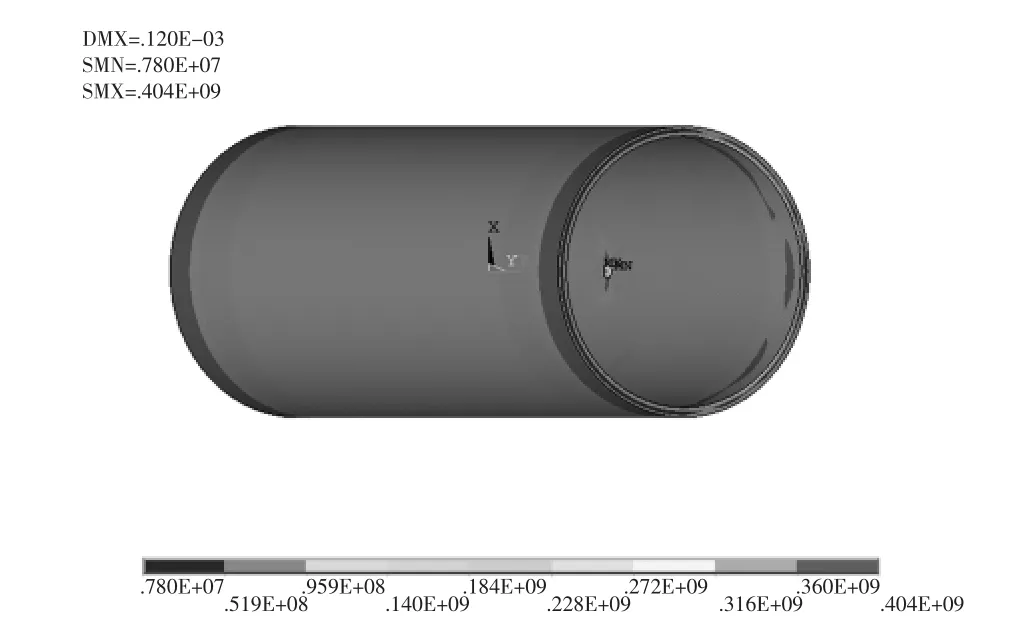
圖2 筒體接管的應力強度分布

在各種工況下，對殼體單元和實體單元接管根部的最大應力強度進行提取和計算，最終得到最大薄膜應力強度值如表3所示。橫向對比殼體單元和實體單元結果不難發現：除軸向力加載工況外，殼體單元的計算結果均大于實體單元的計算結果，尤其是力矩作用下，殼體單元的結果比實體單元的結果要大40%左右。而從絕對數值上講，由于典型軸向力加載對最大薄膜應力的貢獻是各分量中最小的，實際計算中可忽略兩種方法間的差距，因此可認為實際多分量復雜加載下殼體單元的結果較實體單元的結果是保守的，這和經驗及實際中的做法是一致的。

縱向對比各分量對根部最大薄膜應力強度的影響，可以看出內壓的貢獻最大，是作用力貢獻的10倍，是力矩貢獻的4倍。因此內壓對根部最大薄膜應力強度的貢獻是最為顯著的。

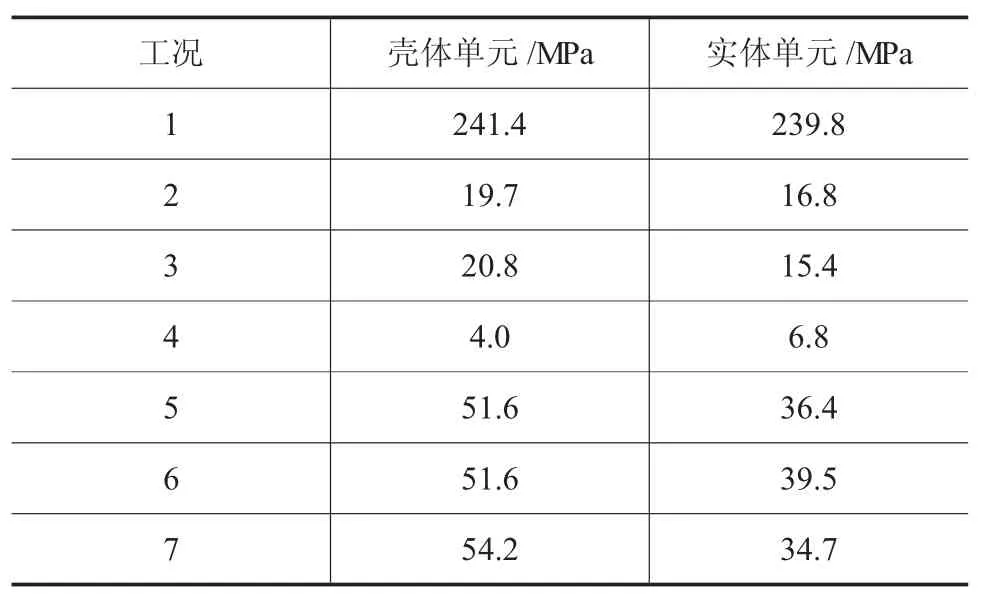
表3 接管根部的薄膜應力強度

3.2 公式法

由于內壓對根部應力強度的影響最大，本文僅就內壓進行討論。表4列出了在10MPa內壓作用下，分別運用薄壁殼體公式和厚壁殼體公式計算的筒體和接管的應力值。

表4 公式計算數值

一般厚度大于半徑的十分之一（即t/R>0.1）的殼體可看作厚壁殼體，否則為薄壁殼體。本例中，接管（t/R=0.104）應屬于厚壁殼體，而筒體（t/R=0.02）應屬于薄壁殼體。橫向比較可看出筒體的兩個結果更為接近，相差0.1%；而接管的數值差距為6.8%。也就是為減少誤差，屬于厚壁殼體的應該用厚壁殼體公式，而屬于薄壁殼體結構的用厚壁殼體公式與薄壁殼體公式結果基本相同。

縱向比較，筒體直徑是接管的11倍左右，內壓作用下的應力是接管的7倍。若將筒體接管根部看作兩者的疊加，那么還需要用兩者的應力和乘以約1.45倍的應力集中系數修正才能得到與有限元模型相近的結果.

4 結束語

本文對筒體外接接管在各種典型受力狀況下的根部應力強度進行了計算和分析。總體說來，運用殼體有限元模型計算得到的結果是最保守的。運用公式法分別計算疊加則需要再乘以一定倍數的應力集中系數進行修正。而對比各典型載荷對根部最大應力強度的貢獻可知內壓的作用是顯著的，其次是力矩的作用。這些結果的對比分析為以后便捷預估筒體接管根部最大應力強度提供參考。

[1]AFCEN.RCC-M[R].2000+2002補.

[2]楊新岐，霍立興，張玉鳳.壓力容器接管區應力集中彈塑性有限分析[J].壓力容器，1997，14（3）：213-217.

[3]桑芝富，李 磊，錢慧林.接管外載荷作用下補強圈結構的應力分析[J].壓力容器，1997，14（3）：218-223.

[4]王勖成.有限單元法[M].北京：清華大學出版社，2003.

[5]單輝祖.材料力學[M].北京：高等教育出版社，2004.

Mechanical analysis of equipment nozzles

SU Hao1,TANG Xingling
（China Nuclear Power Engineering Co.,Ltd.,Beijing 100840,China）

The finite element shell&solid model and formula method estimation have been adopted to conduct the stress analysis to the nozzle on cylindrical body under single variable function.The results show that the result from finite elementshell model is most conservative.The influence of inner pressure to the stress intensity is most obvious under typical loading.The estimation of maximum stress intensity by formula method should multiply certain stress intensity coefficient on the basis of thick wall shell formula.These methods can provide reference for the estimation and evaluation of the nozzle stress intensity in the future.

Cylindrical body nozzles;Stress analysis;Nozzle loads

TH12

A

10.16316/j.issn.1672-0121.2017.02.025

1672-0121（2017）02-0086-03

2016-12-26；

2017-02-04

宿 昊（1988-），男，工程師，從事反應堆結構力學研究。

E-mail：isuhao@163.com