缺失原始數據的單因素方差分析方法研究

于向鴻 肖陽

摘要對缺失原始數據的數據資料進行了方差分析。從方差分析的基本原理入手，對基本統計數據進行反向推理，得到處理間和誤差項的各項離差平方和、自由度以及均方，從而可以實現缺失原始數據下的方差分析，并編寫了SAS程序予以實現整個計算和方差分析過程。

關鍵詞方差分析；缺失原始數據；二次數據；SAS

中圖分類號O212 文獻標識碼A文章編號0517-6611（2017）08-0014-02

Research on the One Way Analysis of Variance with the Loss of Original Data

YU Xianghong， XIAO Yang

（Statistics Office， Graduate School of the Chinese Academy of Agricultural Sciences， Beijing 100081）

AbstractWe completed the analysis of variance without original data. Based on principle of analysis of variance and basic statistics， it was carried out mathematic deduction to obtain sum of square， degree of freedom and mean square of errors and treatments， so analysis of variance could be accomplished in the condition of loss original data. In the end， SAS procedure was programmed to realize the whole process of calculation.

Key wordsANOVA；The loss of original data；Second data；SAS

方差分析（Analysis of Variance，簡稱ANOVA）是英國統計學家Fisher首次在科學試驗中提出的數據分析方析，是一種重要的科研數據的基本統計分析方法，目前在農業和生物學等領域有著廣泛的應用[1-2]。

方差分析法就是利用方差的可分解性，從總變異中分解出組間（處理）變異和組內（重復）變異，并把組間變異與組內變異進行對比，進行顯著性檢驗，從而得到各個處理之間的真實差異[3]。

在科學研究領域，由于時代變遷、人員更替等原因導致原始科研數據丟失，或者公開發表的學術論文中沒有原始數據，而只有各處理的均值、標準差或者標準誤以及重復數等基本統計數據，這樣的數據也被稱作二次數據，數據中大量的原始細節信息已經丟失，要對其進行方差分析較難。

方差分析中最簡單、最常見的是單因素方差分析[4]，所有復雜的方差分析在基本原理上等同于單因素方差分析，筆者以常見的單因素方差分析為例（以下提到的方差分析均指單因素方差分析），通過對方差分析基本原理的分析，對均值、重復數和標準差數據進行了反向推算，最終得到各項的離差平方和、自由度以及均方，實現了缺失原始數據的方差分析。

1方差分析的基本原理

1.1單因子試驗概述

單因子試驗為只考慮1個試驗因子對試驗指標產生影響的試驗，是最常見、最簡單的科學試驗[5]。記因子為A，有r個水平：A1，A2，…，Ar，此處也稱為r個處理。又設在Ai水平下重復進行mi次試驗，i=1，2，…，r，總試驗處理數n=m1+m2+…+mr。記yij為因子A在第i個水平下第j次試驗的觀測值，則它的總平均值為：

=1nri=1mij=1yij=1nri=1mii（1）

式中，i為水平Ai下mi次重復試驗的均值。

1.2離差平方和的計算

這n個數據的變異來源用離差平方和SST來表示：

SST=ri=1mij=1（yij-）2（2）

利用代數運算可將SST分解為2個離差平方和：

SST=ri=1mij=1（yij-i）2+ri=1mi（i-）2（3）

式中，第1個離差平方和稱為組內平方和，又稱誤差平方和，記為SSe；第2個離差平方和稱為組間平方和或因子A的平方和，記為SSA。則有：

SSe=ri=1mij=1（yij-i）2（4）

SSA=ri=1mi（i-）2（5）

SST=SSA+SSe（6）

1.3自由度的計算

總自由度dfT=n-1，因子A的自由度dfA=r-1，誤差項的自由度：

dfe=ri=1（mi-1）（7）

滿足等式：

dfT=dfA+dfe（8）

1.4均方的計算

因子A的均方MSA和誤差項的均方MSe分別為：

MSA=SSAdfAMSe=SSedfe（9）

取F統計量為因子A的均方與誤差項的均方之比：

F=MSAMSe（10）

則此F統計量服從第一自由度為dfA，第二自由度為dfe的F分布。

1.5方差分析表

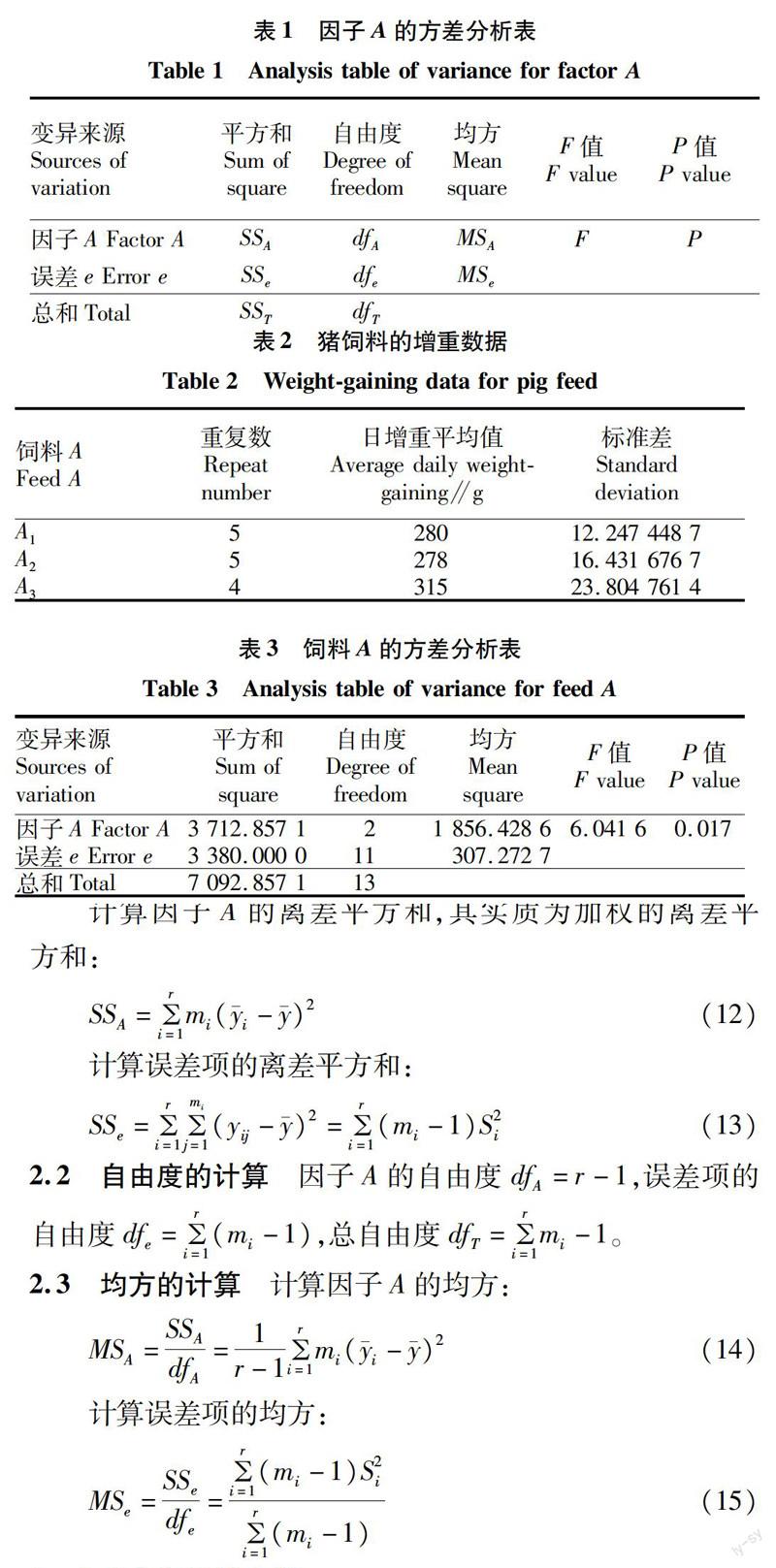
根據方差分析的基本原理，即可在0.05的顯著性水平下對F統計量進行檢驗[6]，得到方差分析表（表1）。

2缺失原始數據的方差分析

對于原始數據缺失的科研數據，通常只給出各處理（即

因子A的水平）的均值、標準差（或方差）或均值的標準誤以及重復數。標準差、方差和標準誤之間可以相互換算，只要知道其中任何1項即可得出其他2項，通常給出的是標準差。該研究以數據給出各處理（r個處理）的均值i、標準差Si和重復數mi（i=1，2，…，r）為例進行分析，方差分析的所有統計量都可以由這幾個基本統計量計算得到。

2.1離差平方和的計算

對于給定的標準差Si，首先取平方轉換成方差S2i。首先需進行總平均值的計算，總平均值其實質為各處理的加權平均值：

=1nri=1mii=ri=1miiri=1mi（11）

計算因子A的離差平方和，其實質為加權的離差平方和：

SSA=ri=1mi（i-）2（12）

計算誤差項的離差平方和：

SSe=ri=1mij=1（yij-）2

=ri=1（mi-1）S2i（13）

2.2自由度的計算

因子A的自由度dfA=r-1，誤差項的自由度dfe=ri=1（mi-1），總自由度dfT=ri=1mi-1。

2.3均方的計算

計算因子A的均方：

MSA=SSAdfA=1r-1ri=1mi（i-）2（14）

計算誤差項的均方：

MSe=SSedfe=ri=1（mi-1）S2iri=1（mi-1）（15）

3方差分析計算實例

3.1實例

考察3種不同配方的飼料（因子A）對豬的育肥效果[7]，試驗指標為豬的日增重（y，單位g），每種飼料飼喂5頭豬，但由于參與第3種飼料試驗的1頭豬因病中途退出試驗，只剩下4頭豬完成試驗。由于某種原因，原始試驗數據缺失，最后只有3種飼料育肥試驗的重復數、平均日增重和日增重的標準差，試驗數據如表2所示。

對上述試驗數據中3種飼料間育肥效果是否存在顯著差異進行方差分析。

3.2方差分析結果

根據公式（11）～（15），可以計算試驗因子（飼料A）和誤差項（e）的自由度、離差平方和、均方以及F統計量和其顯著性P值，可得到如下方差分析表（表3）。

方差分析結果顯示，F=6.041 6，P=0.017，在0.05顯著性水平下，P=0.017（<0.05），表明3種飼料（因子A）間對豬的育肥效果存在顯著差異，還可以進一步進行3種飼料育肥效果均值的多重比較[8]。

4結論與討論

通過對方差分析基本原理進行剖析和推導，以平均值、標準差以及重復數等數據為基礎進行計算，最終可以得到處理間和誤差項的各項離差平方和、自由度以及均方，從而可以實現缺失原始數據一樣的方差分析，使二次數據得到充分利用。

同時運用該方法，對于公開發表的學術論文里的方差

分析結果，在沒有原始數據的情況下也可以進行方差分析的核驗。

該研究只對最常見、最簡單的單因素方差分析進行了分析和推導，得到了缺失原始數據的方差分析，而對于其他更復雜的方差分析在原理上相同，也可以進行類似的分析[10]。

對于試驗指標的均值的多重比較，因為誤差項的均方已經得到，相對就較為簡單，需要進行下一步的均值多重比較即可得到[11]，該研究不再贅述。

結合科研上的實例，運用強大SAS軟件[12]進行編程，實現了缺失原始數據的方差分析的 SAS程序[13]，大大簡化了分析過程，極大地提高了計算效率和準確性。

參考文獻

[1] 郭萍.單因素方差分析在數理統計中的應用[J].長春大學學報，2014，24（10）：1370-1373.

[2] 高卓.單因素方差分析應用的實證研究[J].赤峰學院學報（自然科學版），2014，30（3）：4-6.

[3] 阮敬.SAS統計分析從入門到精通[M].北京：人民郵電出版社，2009：53-54.

[4] 劉加妹，彭景楩.生物實驗數據的單因素方差分析[J].動物學雜志，2001，36（6）：34-37.

[5] 茆詩松，周紀薌，陳穎.試驗設計[M].北京：中國統計出版社，2004：13-22.

[6] 蓋鈞鎰.試驗統計方法[M].北京：中國農業出版社，2006：101-103.

[7] MIROSLAV K，LAMBERSON W R.Biostatistics for Animal Science[M].Cambridge：CABI Publishing，2004：212-226.

[8] 高惠璇.實用統計方法與SAS系統[M].北京：北京大學出版社，2001：43-46.

[9] 胡小平，王長發.SAS基礎及統計實例教程[M].西安：西安地圖出版社，2001：116-122.

[10] 高惠璇.SAS系統：SAS/STAT軟件使用手冊[M].北京：中國統計出版社，1997：250-263.

[11] SAS Institute Inc.Statistic II：ANOVA and Regression[M].Kerry，USA：SAS Institute Inc.，2005：156-161.

[12] 夏坤莊，徐唯，潘紅蓮.深入解析SAS：數據處理、分析優化與商業應用[M].北京：機械工業出版社，2014：334-340.

[13] 劉榮.SAS統計分析與應用實例[M].北京：電子工業出版社，2013：56-58.