激光毀傷中的多光譜測溫技術研究

秦亞樓， 李偉， 楊春平， 韋焱斌， 彭真明

(1.電子科技大學 光電科學與工程學院, 四川 成都 610054; 2.電子科技大學 信息與通信工程學院, 四川 成都 610054)

0 引言

目前激光技術在毀傷方面的應用越來越普遍，如在工業上使用激光對材料進行切割、在軍事上使用激光對目標進行打擊等，上述領域中對激光毀傷時分析與控制精度的要求越來越高。對激光毀傷的分析，通常需要目標區域的溫度、形態等狀態變化，因此激光毀傷目標區域的溫度是分析毀傷狀態中必不可少的一部分。測量激光毀傷區域的溫度時使用接觸式測量會因為激光照射、溫度改變而影響實際測得的溫度，所以激光毀傷時的溫度測量應使用非接觸測溫，非接觸測溫方法主要包括比色測溫法及多光譜測溫法。比色測溫法需要測量兩個波長下的光譜強度，然后計算兩個波長下光譜強度的比值、得到測量溫度。

實際測量光譜不僅包含一種溫度的光譜，通常是一段溫度范圍內的光譜疊加，測量光譜包含非目標光譜外的其他溫度光譜及背景光譜信息，比色測溫法測量較為臨近兩波長下的光譜強度，提高比色測溫法的測量精度主要是通過減少非目標光譜的干擾。

多光譜測溫法測量某個波段范圍內的光譜強度分布，并與不同溫度下的光譜輻射強度相比較，將與測量輻射光譜曲線殘差最小的理論光譜輻射曲線認為是待測溫度的光譜曲線，將此理論溫度認為是目標溫度。多光譜測溫法受其他溫度輻射光譜及背景光譜的影響更大，因此在與理論輻射曲線比較之前必須要對測量光譜進行預處理，以減小非目標光譜的影響。

國內外關于比色測溫法、多光譜測溫法的研究多用于分析溫度分布。比色測溫法主要是通過削減非目標光譜的影響、提高測量波段個數及精度，從而提高比色測溫精度；多光譜測溫主要是通過對測量光譜的反演，得到目標區域的溫度分布。近年來國內外在多光譜測溫技術方面研究的進展主要是：Rodiet等[1]提出單光譜、多光譜在測量輻射光譜時選擇最佳波長用于測溫； Daniel等[2]提出了一種利用曲線擬合技術的多光譜測量方法，這類目標的溫度范圍為800～1 200 K，目標周圍溫度為1 273 K；Gao等[3]利用一種高分辨率光纖多光譜高溫計在狹小空間內測量700～1 200 K的溫度，并利用遺傳算法對相應的模型進行了優化，保證測量誤差<0.44%；Bouvry等[4]使用多光譜輻射測溫法，并假設在波長1.00～1.30 mm和1.45～1.60 mm范圍內光譜發射率剖面的發射率為常數，溫度在700～850℃之間，測得的溫度誤差范圍為±4℃；朱澤忠等[5]提出了一種新的能夠同時高精度測量目標的瞬態激發溫度和輻射溫度的方法，提高了測溫精度；Yang等[6]分析了900～1 700 nm波段下的光譜以及不同波段高溫黑體輻射光譜的光譜特性；王家寧等[7]提出了解決拉曼測溫系統后端光譜信號采集速度過慢和減弱噪聲的方法；劉慶明等[8]研究了爆炸過程對光譜測溫的影響，并對其結果進行了分析；郝曉劍等[9]提出了利用外推法拓寬藍寶石光纖黑體腔高溫傳感器測量范圍的方法；蔡紅星等[10]在強激光毀傷過程中使用多光譜技術測量溫度分布，測量溫度區域在2 400 K附近；李云紅等[11]提出了通過比色測溫實現中低溫(50～400℃)物體溫度測量的方法，搭建雙波段系統對中低溫的測量，測量誤差在3℃以內；符泰然等[12]將三波長輻射溫度測量方法拓展到譜段溫度測量。

激光毀傷過程中，通常目標毀傷區域、測量光譜輻射區域大小有限，且毀傷區域溫度分布較為規律，多光譜測溫技術較適用于激光毀傷中目標區域的溫度測量。本文實驗通過在傳統多光譜測溫技術基礎上對不同溫度區域光譜的疊加分析，以提高測溫精度。本文研究了激光毀傷時毀傷區域的輻射光譜，并對毀傷區域下的多光譜測溫技術進行了優化，這種優化方法為深入研究激光毀傷區域的狀態分布及狀態變化提供了參考。

1 多光譜輻射測溫及比色測溫理論技術

多光譜測溫技術理論基礎是普朗克黑體輻射定律，如(1)式所示：

(1)

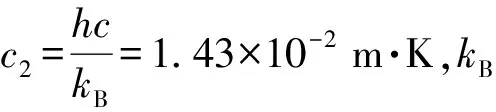
當目標溫度大于0 K時，目標以電磁波譜形式向外輻射能量。由(1)式中可知，隨著溫度T的升高，輻射強度也會變大。實驗使用光譜儀測量波長范圍為700～1 400 nm，1 000 K下在此波段內波長與輻射光譜強度的關系如圖1所示。從圖1中可以看出：在這個波段的輻射強度呈快速上升趨勢，不同波長下輻射強度的比例也較大，根據(2)式可知在這種情況下比色測溫法的測溫精度是較高的，該波段也較為適合多光譜測溫法。

(2)

式中：M1表示在波長λ1下的光譜輻射強度；M2表示在波長λ2下的光譜輻射強度。

從圖1中可以看出，在700～1 400 nm波段內，輻射強度隨波長的增加而變大，并且在1 000～1 400 nm波段內的光譜輻射強度快速增大，在1 000～1 400 nm波段內選取比色測溫的波長及輻射強度可以保證比色測溫的精度。

多光譜測溫法對測量光譜進行反演分析時，使用最小二乘法計算測量光譜與理論光譜的殘差，當殘差最小時，認為該理論光譜的溫度為測量溫度。設測量不同波長光譜輻射強度為Mi，計算測量輻射強度與理論輻射強度Mstd的方差，如(3)式所示：

∑(Mi-Mstd)2.

(3)

若使(3)式的方差最小，則應對其求導數，得

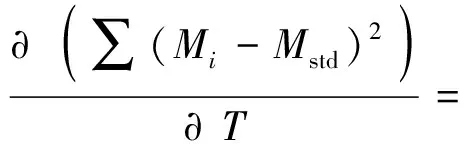
(4)

由(4)式可知，方差最小要求測量的輻射光譜強度積分與理論輻射光譜強度積分相差最小，即

Ma=Mt-Mb，

(5)

式中：Ma表示減少背景輻射影響的光譜輻射強度；Mb表示背景輻射光譜輻射強度；Mt表示測量光譜輻射強度。

多光譜測溫技術要求測量光譜與理論光譜強度積分的差值最小，則在使用光譜反演溫度時，需要排除目標光譜中的背景輻射光譜。按(5)式計算可以減少測量光譜中背景光譜的影響，此時積分相差最小的理論溫度為測量溫度。

2 激光毀傷中的多光譜輻射測溫

本文研究的多光譜溫度反演技術不考慮遠距離情況下大氣傳輸對高斯光束的影響，將光譜發射率設為定值0.85，并且在高溫情況下材料最終照射在毀傷區域上的激光光束呈高斯分布。

本次模擬實驗主要研究高斯激光對目標區域的影響，高斯激光的光束能量按二維高斯函數分布。二維高斯函數為

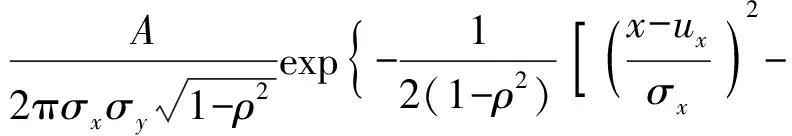
(6)

式中：σx為x方向位置的標準差；σy為y方向位置的標準差；ux為x方向中心點坐標；uy為y方向中心點坐標；ρ為x方向光束能量與y方向光束能量的相關度；A為函數的幅值。

由(6)式可知，高斯光束能量分布從光束中心向光束邊緣逐漸減小，目標區域溫度分布包含不同溫度。在溫度反演時，可以將溫度分布模擬為梯度分布，不同溫度梯度區域的光譜疊加為測量的輻射光譜。因此當(6)式中的參數取適當值時，模擬高斯光束的能量分布如圖2所示。

圖2顯示由內向外高斯光束能量逐漸減弱，且能量分布較為規則，光譜儀所測量區域為中心高溫區域。因為目標毀傷區域通常是較為規則的近似圓形，所以可以將目標區域的溫度分布簡化為溫度不同的兩部分，如圖3所示。

圖3中顯示測量區域整體溫度較高，且相差不大。實際測量光譜是不同溫度輻射譜的疊加，假設目標區域最高溫度是1 500 K，也是測量的目標溫度，目標區域中處于1 500 K溫度下的區域占目標區域總面積的80%，而處于1 400 K溫度下的區域占目標區域總面積的20%，此時不同溫度區域面積比為8∶2，即1 500 K與1 400 K的輻射光譜按8∶2的比例疊加。 同時將上述疊加光譜與按7∶3比例疊加的輻射光譜進行比較(見圖4)，分析不同比例光譜輻射強度與疊加比例的關系。

由圖4中的光譜數據可以看出，在疊加光譜中，高溫區域比例所占越高，光譜輻射度越大。將疊加光譜作為目標區域的測量光譜，對疊加光譜進行比色分析與多光譜分析可知：比色測溫法計算后的溫度為1 490 K，與1 500 K相差為10 K，且相差溫度大小受選取波長間隔影響；同樣直接用多光譜測溫法對疊加光譜進行分析，計算溫度為1 483 K，與1 500 K相差17 K左右，相比于比色測溫法，直接使用多光譜測溫法對測量光譜進行分析，其誤差是較大的。但若將其不同溫度的比例考慮進來，則根據(7)式：

Msum=aMT2+bMT1，

(7)

使用多光譜測量技術反演測量光譜與疊加光譜，比較兩種光譜反演的測溫誤差。選取反演誤差小的疊加光譜作為實際光譜，將此疊加光譜的高溫部分作為測量溫度。根據此方法反演得到的溫度數據相比同樣情況下的比色測溫法結果可以減小4～10 K左右的誤差，相比較未改進的多光譜測溫法可以減少20%以上的誤差。

同樣目標區域不同溫度區域比例的測量也是有誤差的，但是在激光毀傷過程中，由于強激光能量較高，毀傷區域的溫度及損傷明顯區別于其他毀傷外區域。毀傷過程中其不同溫度區域的面積測量誤差一般不會超過實際面積的10%. 根據上述對毀傷區域溫度分布的假設，雖然目標毀傷區域中1 500 K溫度區域與1 400 K溫度區域的實際面積比例為8∶2，但兩次測量的不同溫度區域面積比分別為7∶3、9∶1. 根據(7)式及傳統多光譜測溫法的分析，從1 483 K的溫度處開始進行光譜的重新計算，將不同溫度的光譜輻射度按相應比例疊加，光譜輻射度疊加后的光譜輻射度數據分別如表1～表3所示。

表1 疊加比例為7∶3的光譜輻射度疊加表

表2 疊加比例為8∶2的光譜輻射度疊加表

表3 疊加比例為9∶1的光譜輻射度疊加表

表1～表3包含了按相應比例疊加后的光譜輻射強度數據，用該數據與預處理后的光譜數據進行比較，其中差值絕對值最小的光譜輻射度數據即為真實溫度下的光譜輻射度數據。將在不同比例疊加下反演出來的溫度與傳統多光譜測溫法反演的溫度、比色測溫法反演的溫度及標準溫度進行誤差分析，結果如表4所示。

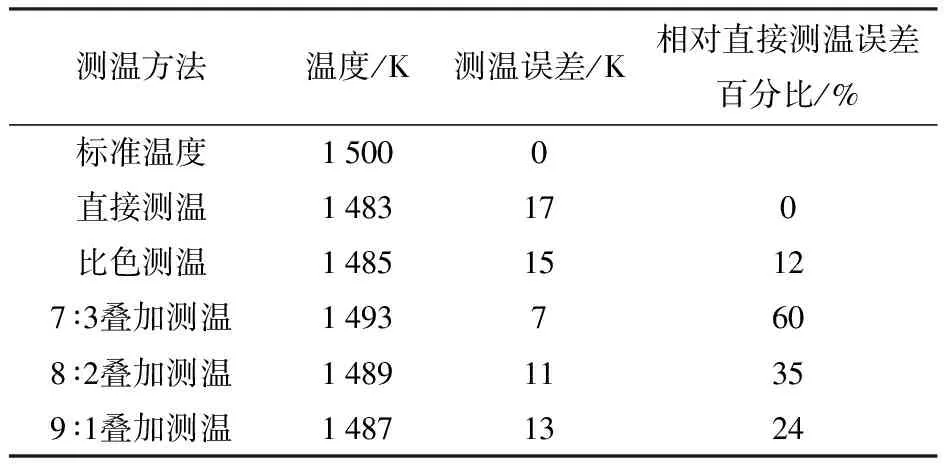
表4 不同溫度比例疊加測量方法與傳統方法的數據對比表

從表1～表4中可以看出：使用(4)式對光譜直接反演，反演溫度為1 483 K；疊加后輻射光譜的反演溫度分別為1 493 K、1 489 K、1 487 K，與傳統多光譜測溫法相比，測溫誤差分別縮小10 K、6 K、4 K. 上述3種比例疊加后的光譜，其中以面積比7∶3進行疊加的光譜所反演的溫度最為準確。

按照上述方法，假設測量得到毀傷區域高溫區域與低溫區域為3 500 K與3 400 K，面積比例為8∶2，將輻射光譜按上述方法中面積比分別為7∶3、8∶2、9∶1進行疊加。對疊加后的輻射光譜進行分析可知，其反演精度相比1 500 K下測溫精度較差，但相比于傳統的多光譜測溫方法，對相應疊加輻射光譜的溫度反演仍能縮小測溫誤差。

3 結論

本文基于普朗克理論及多光譜分析方法分析了700～1 400 nm波段范圍內的不同溫度光譜輻射度變化規律，及高斯激光對目標區域毀傷時的毀傷區域溫度分布規律。根據實際實驗及理論對不同溫度區域的面積比例進行模擬，結合不同溫度區域的面積比例，按相應面積比例進行輻射光譜的疊加。采用多光譜測溫技術對疊加前、后輻射光譜進行反演，總結每個光譜下的溫度反演精度。得到主要結論如下：

1)在近距離激光毀傷或不考慮大氣影響的條件下，通過之前對不同溫度面積比例疊加的溫度反演分析可知，疊加光譜計算得到的溫度誤差最低可以縮小24%的誤差，最大可以縮小60%的誤差，并且在3 500 K的溫度下進行模擬，其反演誤差大小與1 500 K下的反演誤差不同，測量誤差仍受毀傷區域溫度的影響。

2)本文所提方法為激光毀傷時毀傷區域溫度分布的測量提供了一種思路，有助于提高毀傷區域中不同溫度面積分布的測量精度。