泊松曲線法在高鐵橋梁工程沉降預測中的應用

杜紅霞

[摘要]沉降預測與評估是高速鐵路無砟軌道施工前必須進行的工程環節，常用的沉降預測方法僅適用于荷載穩定條件下的沉降預測，而全過程沉降量預測，泊松曲線法能很好地反應結構物施工全過程的沉降與時間的關系。本文結合工程實例，將泊松曲線法應用于高速鐵路橋梁工程的沉降預測，沉降預測結果顯示，泊松曲線法沉降預測精確度較高，預測的最終沉降與實測沉降比較接近，沉降預測效果良好，表明全過程沉降量預測的泊松曲線法對于高速鐵路橋梁工程具有很好的適用性。

[關鍵詞]沉降預測；泊松曲線法；高速鐵路；相關系數；精確度

高速鐵路客運專線線路的平順和穩定是實現列車快速、安全和舒適的保障，這就要求施工階段必須嚴格控制線下結構物的沉降變形，尤其是工后沉降量。而目前在設計階段還無法準確預估沉降變形和有效地控制工后沉降，沉降計算最常用的方法是結合土工試驗的一維固結理論，但地基沉降實際情況很復雜且屬于三維課題，理論計算結果往往與實測結果相距甚遠。因此利用沉降觀測資料采用曲線擬合的方法推算后期沉降和最終沉降有著重要的現實意義。

土體不再加載時，由于土體尚未固結結束以及流變，沉降量將繼續增大，但沉降速率逐漸遞減：

4）沉降趨于穩定階段

隨著時間進展，沉降將達到極限穩定狀態。通過工程實例也發現，當時間足夠大時，沉降會逐漸平穩并趨于收斂。

泊松曲線所描述的“S”特征與上述地基沉降非常相似，因此，可以用泊松曲線來預測地基沉降隨時間的變化規律。

1引言

常用的沉降預測方法，如雙曲線法、指數曲線法、Asaoka法和灰色理論等，僅適用于荷載穩定情況下的沉降預測，因此擬合起點只能選取在橋梁工程主體完工之后。而全過程沉降量預測的泊松曲線法由于能夠利用前期觀測資料，能很好地反應結構物施工全過程的沉降與時間的關系，

泊松曲線被稱為飽和曲線，它反映了事物從發生發展到成熟，最終趨于極限或者飽和的過程。在沉降預測中，泊松曲線的表達式為

（1）

式中：s為t時刻的累積沉降量/mm；K為預測的最終沉降量/mm；a為瞬時沉降速率；c為待求參數。2

泊松生長曲線的特點

由式（1）可知，泊松生長曲線模型具有以下特點：S-t曲線不通過原點。

2.1不通過原點的機理分析

對于飽和土來說，在荷載作用下會迅速產生瞬時沉降，即為初始沉降，是由負剪區域的剪應變在土體體積不變的情況下引起的變形。在荷載中心線下，滲透性很低的黏土幾乎不發生排水，土體同時發生側向膨脹和垂直壓縮。對于非飽和土，在荷載施加后孔隙中的氣體可被壓縮，由于空隙被壓縮使得土骨架也產生變形，因而初始荷載由氣體、土骨架和水三者共同承擔。隨著氣體和水的排出，骨架繼續被壓縮，應力將逐漸轉移到土骨架上，由此在沉降曲線初始點會出現瞬時的沉降。綜上所述，由于初始沉降的存在，S-t曲線不通過原點。

2.2“s”形機理分析

沉降曲線不通過原點是由于瞬時沉降的存在，地基的總沉降包含瞬時沉降、固結沉降和次固結沉降三部分。隨著時間和荷載的變化。固結沉降和次固結沉降的變化可以分為如下幾個階段：

1）沉降量近似線性增加階段

土體在剛加載時仍然處于彈性狀態，隨著時間和荷載的增加，沉降量的發展呈近似線性：

2）沉降速率增加階段

土體在繼續加載時逐漸進入到彈塑性狀態，土體的沉降量和沉降速率不斷加大：

3）沉降速率遞減階段

3非線性求解過程

泊松曲線模型為非線性模型，直接求解非常困難。本文采用最小二乘法對模型中的參數K、a和c進行反演優化，以沉降計算值和實測值的絕對誤差建立如下目標函數：

（2）

（2）以J為最小值作為控制條件，運用MATLAB程序內置的lsqeurvefit函數迭代求得K、a和c值，進而得到泊松曲線的表達式；

（3）求出任意時刻t的預測沉降量S_t。

4工程實例分析

本文選取的沉降觀測區段為某客運專線鐵路特大橋180#墩至205#墩為試驗區段，橋址范圍地勢平坦，橋樁基均為嵌巖樁，最小嵌巖深度均超過5.0m。

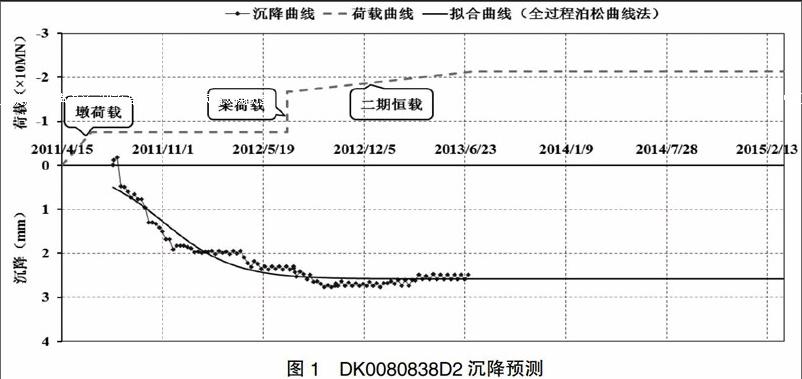
客運專線鐵路無碴軌道鋪設條件評估技術指南指出，擬合精確度良好的相關系數不小于0.92，表明擬合曲線與實測沉降曲線的趨勢吻合較好。采用泊松曲線法，對該區段的52個觀測點的原始觀測數據進行全過程的沉降預測，相關系數R≥0.92的沉降觀測點數及百分比見表1。圖1給出了典型觀測點DK0080838D2的荷載-沉降-時間關系曲線，

由表1和圖1可知！

（1）對比于Asaoka法、灰色理論、雙曲線法和指數曲線法沉降預測方法，泊松曲線法52個測點的相關系數均大于0.92，沉降預測精度得到了顯著提高。

（2）所有觀測點的預測最終沉降與實測沉降均比較接近，典型觀測點的實測沉降曲線和預測曲線吻合度較高，沉降預測效果良好。

由此可知，全過程沉降量預測的泊松曲線法對于高速鐵路橋梁工程具有很好的適用性，

5擬合參數初始值的取值范圍

在泊松曲線非線性求解過程中，首先需要給定參數K、a和c的初始值，而合適的初始值將會減少MATLAB程序迭代次數，大大提高運算速度和沉降預測結果的準確性。表2給出了試驗區段52個測點通過非線性求解最后得出的擬合參數結果范圍。

由式（1）可知，K為模型預測的最終沉降量，a為瞬時沉降速率，c為待求參數。因此，客運專線鐵路橋梁工程沉降觀測點擬合參數K、a和c初始值的取值，應依據觀測點累計沉降和沉降速率來確定，如果確定某個參數的取值比較困難，可以參考表2并結合觀測點自身沉降特點綜合確定。

值得說明的是，表2中的擬合參數計算結果范圍僅僅是橋梁工程試驗區段觀測點的統計結果，對于其他結構物，如路基、隧道和過渡段等，并不一定具有參考意義。

6結語

綜上所述，泊松曲線法由于能夠利用前期觀測資料，沉降觀測區段52個測點的相關系數均大于0.92，擬合曲線與實測曲線吻合度較高，表明全過程沉降量預測的泊松曲線法對于高速鐵路橋梁工程具有很好的適用性。

[責任編輯：王偉平]