基于遺傳算法與模擬退火算法在多重DNA序列比對中的應用研究

閆 磊,馬 健,董 輝,高 夢

(亳州職業技術學院 信息工程系,安徽 亳州 236800)

基于遺傳算法與模擬退火算法在多重DNA序列比對中的應用研究

閆 磊,馬 健,董 輝,高 夢

(亳州職業技術學院 信息工程系,安徽 亳州 236800)

序列比對是將蛋白質中的基因或氨基酸進行對齊的動作,目的是要找出兩序列的相似程度,而多重序列比對則是同時比對多個DNA或蛋白質序列,找出此序列群組中最佳的比對結果.本研究結合遺傳算法及模擬退火算法,先利用遺傳算法優化種群的概念,隨著世代演進逐漸產生近似最佳解,再利用模擬退火算法進行小區塊內的比對修正.實驗結果顯示,利用遺傳算法與模擬退火算法的結合,使得遺傳算法在跳脫局部最佳解的時候能有更大空間移動,而且也讓模擬退火算法能有效解決經由遺傳算法初步比對之后所產生的不良區域.兩種算法結合的序列比對結果比任何單一算法的結果好,因此可以提升整體比對效果,將來能夠為生物學家在判斷未知序列功能時提供適當的幫助.

序列比對;多重序列比對;遺傳算法;模擬退火算法

0 引言

對生物學家而言,探索蛋白質的序列對于細胞功能的影響、推測未知蛋白序列的功能、或比較不同的兩個生物中的相似基因之間的差異時,序列的比對都成為不可或缺的一項重要技術.因此近年來在生物學中,序列比對成為一項重要的技術之一,對于蛋白質序列的比對、蛋白質結構的預測、DNA及MRNA的比對以及利用蛋白質序列搜尋DNA序列等方面都具有廣泛的應用.而由序列比對所拓展的多重序列比對,對于生物學家而言更是一項困難且具挑戰性的任務,因為多重序列比對其計所需的時間復雜度將隨著序列數量的增加而呈指數性的成長,所以現在有許多算法應用在此領域.

對于只有兩條序列的比對,利用動態程序規劃可以達到最好的結果.然而利用動態程序規劃算法雖然能夠得到較好的結果,但在序列數量以及長度都增加的同時,對于計算機的計算資源會急劇的提高[1].此外,過去的研究也有利用遺傳算法結合動態程序規劃的方式進行比對,但仍有許多算法在處理這種問題上具有其優點,如模擬退火算法在處理解空間較小的問題上具有良好的表現.本研究使用沒傳算法及模擬退火算法所結合的算法來進行比對,并且對遺傳算法以及模擬退火算法分別進行比對結果來比較,最后將模擬退火算法的概念引入遺傳算法中進行比對,使得遺傳算法在脫良局部最佳解的時候能有更大空間的移動,因此達到對比分數更高的序列比對[2].

本研究利用了遺傳算法及模擬退火算法,先進行兩者應用于多重序列比對的結果,再利用遺傳算法輸出的結果作為模擬退火算法所需序列的基礎輸入序列進行比對的調整,經過兩種算法的運算之后,希望能夠與過去專家所提出的研究能夠達到相近的結果,并且與動態程序規劃進行比對的結果能夠相近.

1 序列比對

圖1 未插入間隔于插入間隔序列比對的比較

生物序列比對是一種比較兩個或多個DNA、RNA或蛋白質序列,并嘗試找出序列中的一連串或單一的對應字符的方法.最常見是將兩條序列并排成兩行,將序列中相同或相似的區段置于相同的字段,而無法比對的字符則在各自的序列中利用插入間隔或產生錯誤.在最佳比對的情況下,插入間隔(gap)“-”可以讓序列具有更好的比對結果,而間隔的出現就表示在序列演化的過程中發生了刪除或插入的情況[3].如圖1(a)所示,兩個DNA序列的比對在還沒插入“-”之前,序列A與序列B具有許多的比對錯誤的部分,在圖1(b)的部分即由插入了“-”而使得整組序列達到比較好的比對結果.

1.1 全局比對

全局比對是嘗試比對在序列中的每一個元素,即其比對是從序列的最前端到序列的最末端,目的是要找出兩序列的相似程度.Needleman和Wunsch于1970年所提出的動態程序規劃是一種序列全局比對的算法,且是首次將動態程序規劃應用于序列比對領域上所開發出的一種方法,如圖2(a)為全局比對[4].

1.2 區域比對

區域比對是尋找兩序列中最相似的子序列或能夠達到最高比對分數的序列片斷,其目的是找出特定的基因片段或功能序列,Smith和Waterman于1981年所提出的動態程序規劃便是一種序列區域比對的算法,如圖2(b)為區域比對.

(a)全局序列比對 (b)區域序列比對

2 算法

2.1 遺傳算法

遺傳算法(genetic algorithm)最早在1960年由Holland 所提出,直到1975年Holland所著作的“Adaptation in Natural and Artificial System”奠定了遺傳算法的基礎.主要是利用模仿自然界中生物的演化過程作為求解問題的一種方法,通過基因的選擇、母代與子代的篩選,以及使用適應函數來仿真達爾文進化論中物競天擇的部分.簡單來說,遺傳算法可說是一種不斷嘗試錯誤、淘汰不良母代以及選擇優良后代的一種過程.

對于過去研究人員利用遺傳算法來進行序列比對的處理的方式,由于單純使用遺傳算法在序列比對問題常常會產生次最佳解,因此通常都結合了多種方法,如表1所示.利用遺傳算法解決序列比對問題的步驟包括:初始化序列、產生母群體并且進行競爭式選擇、進行交配、進行突變、刪除間隔字段、取代族群中的個體與結束演化等方面.

表1 應用遺傳算法于序列比對的研究

2.2 模擬退火算法

模擬退火算法的概念是從物理學中所延伸出來,主要是指模擬固體加熱至高溫之后,其組成的結構會變成液態結構,并且此時結構分子的活動力較強,分子可以隨機跳動的距離也較大.隨著溫度的下降,組成的結構分子也逐漸穩定下來,此時可以跳動的距離也逐漸縮小,形成這個階段的熱平衡,然后重復進行降溫、結晶的動作并排列成固體狀態,而最后穩定的狀態也就是最佳解[5].此方法中最重要的部分即為溫度的調控,若溫度下降過快則可能會導致產生區域最佳解.盡管模擬退火算法對于優化問題求解的過程較緩慢,過去仍有許多研究已經應用于多重序列比對的領域,利用模擬退火算法解決序列比對問題的步驟包括:初始化序列、適應成本的計算、溫度及降溫的參數設定、間隔跳動.

2.3 遺傳算法與模擬退火算法結合

圖3 遺傳算法與模擬退火算法結合流程圖

由于遺傳算法的求解過程中需要產生挑選可用的母代族群,且族群數量也是進行遺傳算法時必須的參數,而模擬退火算法則是比較更新前與更新后彼此狀態的成本差異,就產出的解數量來說,遺傳算法的族群中每個染色體都代表著一個解,而模擬退火算法每次針對一個解進行修正.因此在結合這兩種算法時,本研究先利用遺傳算法產出模擬退火算法所需的初始序列,接著進行模擬退火算法中的移動方法來尋找是否有表現更好的解存在[6].圖3為結合兩種算法之后的比對流程.

3 實驗結果與分析

3.1 實驗資料來源

本研究采用某生物信息中心的部分數據,在收集的數據資料中選取8個數據集,為了整理出與過去文獻中所提到不同的間隔插入方式,先進行序列之間彼此差異程度的計算,方法是計算數據集中各個序列中四種字符的總數以及最大差距,并且利用最長與最短序列的差距來計算出所需插入間隔的數量,各個數據集的差距如表3.利用表2中的序列資料及表3的序列內容分析,可以發現部分的數據集中如S3、S7,各個序列之間字符的彼此差距數量并無非常明顯,且數據集中最長序列減去最短序列的差距也相差不多,因此本研究在實驗設計中加入了由此兩項數值所計算出的間隔插入數量.

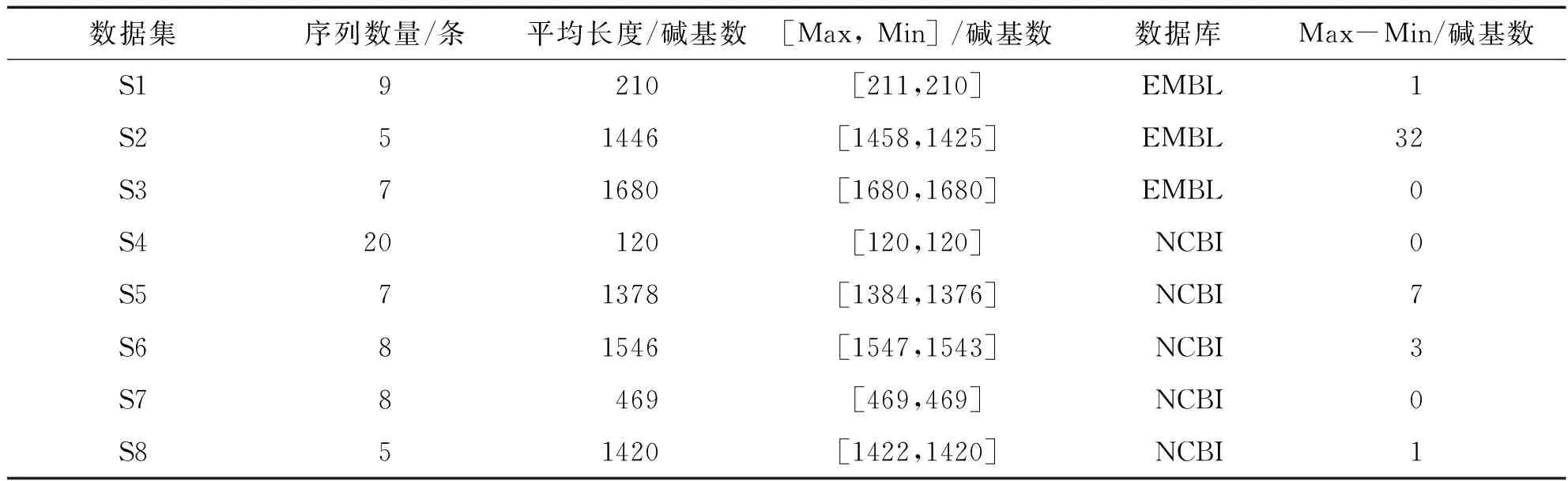
表2 DNA序列原始數據

表3 各個序列的字符差距最大數目與平均差距

續表3

注:表3中A,T,G,C表示堿基

3.2 參數設置

進行遺傳算法以及模擬退火算法時,其中的參數設定將會影響到多重序列比對的結果.因此在此階段先將各個算法所需的參數做分組配置,作為實驗的分組依據,同時并參考了過去的文獻作為參數設定的依據.表4為遺傳算法所需各種參數如族群大小、交配率、各個突變操作數的突變率及矩陣延伸長度的設定,其中Max代表序列群組中長度最長的序列,Min代表序列群組中長度最短之序列, extension代表整個序列群組中四種字元最大最小值的差異,利用表3中的數據計算所得.表5為模擬退火算法中接受率、初始溫度、凝固溫度以及降溫參數的設定.

表4 遺傳算法數設定

表5 模擬退火算法參數設定

3.3 實驗結果與分析

(1)遺傳算法與動態規劃算法預測結果分析

通過上面算法的分析,本文先使用遺傳算法與動態規劃算法組合對DNA多重序列進行比對.首先設置遺傳算法參數,利用交叉操作產生實驗數據,再利用動態規劃算法對遺傳算法進行優化,在較小范圍隨機產生組態,并對每一組進行優化,提高對DNA序列比對的效率,如表6所示.

表6 遺傳算法與動態規劃算法DNA序列預測結果

(2)遺傳模擬退火算法對DNA序列比對分析

本研究首先使用遺傳算法進行多重序列比對,利用表4中的參數設定,各個組態分別利用交叉參數設置產生實驗組別,共產生 27個實驗組態,并選取S2對每個組別各進行五次之后得出最佳的參數設置.利用此參數進行8次實驗且比較之后所得出的最佳配對分數、平均配對分數以及平均比對時間,具體如表7所示.而由此結果得到在本研究的流程中,對于遺傳算法最佳參數設計分別是:交配率為80%、突變率為20%、族群大小為20條、世代數量為15,000代以及矩陣延伸長度為Max×1.

表7 遺傳算法的多重序列比對結果

接著第二階段進行本研究所使用的模擬退火算法進行多重序列比對,利用表5的參數設定,各個組態分別采取交叉參數設置產生實驗組別,并利用數據集S1進行8次實驗后得出的最佳參數設置,且用此參數對各數據集進行五次實驗之后所得出的最佳配對分數、平均配對分數以及比對時間，具體如表8所示.由此表得到的模擬退火算法最佳參數設計分別是初始溫度為100℃,降溫參數為 3℃,接受率為80%.

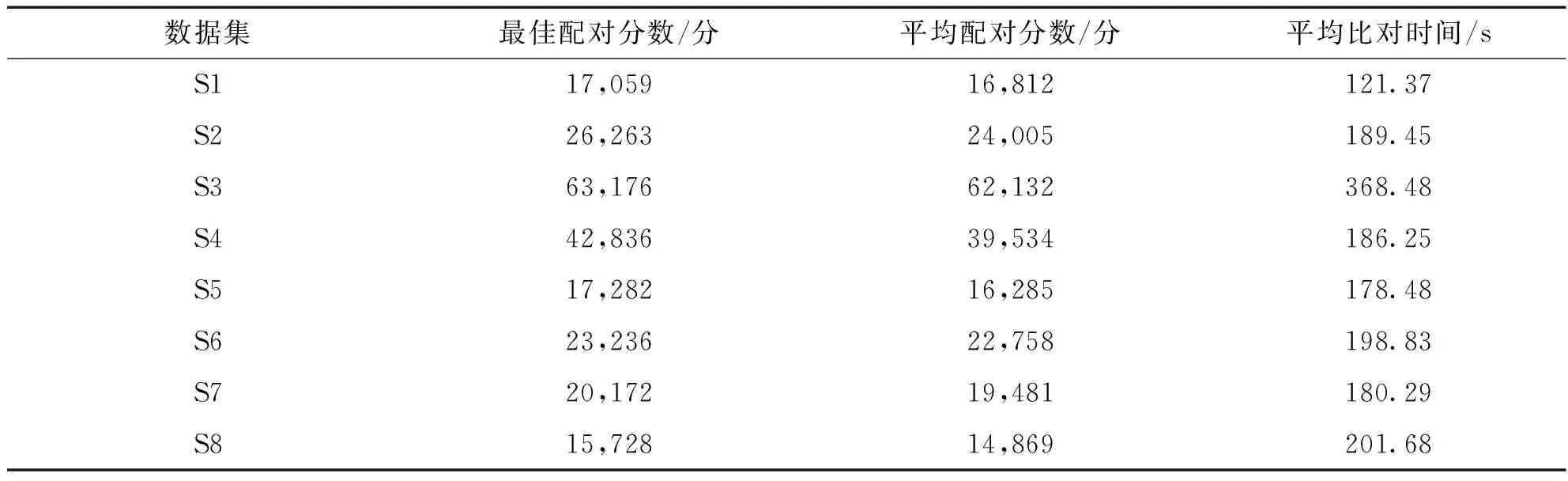
表8 模擬退火算法的多重序列比對結果

兩種算法演算完之后,接著進行第三階段的流程.利用遺傳算法進行比對所得到的解序列作為下一個模擬退火算法流程中所需的初始序列,并改變第二階段模擬退火算法中間隔跳動操作數作用的位置與范圍,而其參數設定分別采用遺傳算法以及模擬退火算法的最佳參數設置,其整體的比對結果如表9所示.

表9 遺傳算法結合模擬退火算法的多重序列比對結果

總之,通過兩種算法對DNA序列比對的實驗結果表明,本研究利用遺傳算法與模擬退火算法結合在多重序列比對上能夠達到不錯的修正結果,在數據集S1與S5中甚至能夠達到相當的比對結果.在遺傳算法中所必須被設定的各項信息,如間隔插入數量、突變率以及交配率等,都與產出的結果相關,若能夠加強在遺傳算法中各個操作數的使用方法以及執行程序,對于近似最佳解的收斂將具有相當程度的改善.

4 結 語

本研究利用遺傳算法的物競天擇的概念,隨著世代演進所逐漸產生的近似最佳解,接著再利用模擬退火算法進行小區塊內的比對修正.實驗結果表明,利用遺傳算法與模擬退火算法的結合,其比對結果都比任何單一算法的結果好,通過結合也可讓模擬退火算法有效的解決經由遺傳算法初步比對之后所產生的不良區域,進而修正且更進一步提升整體比對的效果.

[1]朱彥廷.用遺傳算法求最小生成樹[J].瓊州學院學報,2012,19(2):32-35.

[2]馬健.決策樹算法對電子商務交易信任機制的應用研究[J].河北北方學院學報,2015,31(5):36-39.

[3]張冰龍,徐建敏,江浩.基于模擬退火的DNA遺傳優化小波多模盲均衡算法[J].電子技術應用,2016, 42(2):88- 91.

[4]李志亮,羅芳.基于初始值優化的灰色馬爾科夫鏈預測模型研究[J].海南熱帶海洋學院學報,2016,23(5):55 -59.

[5]崔光照,李小廣,張勛才,等.基于改進的粒子群遺傳算法的DNA編碼序列優化[J].計算機學報, 2010, 33(2):311-316.

[6]王哲河,林越,張僑.Dijkstra算法在三亞旅游線路規劃中的應用[J].瓊州學院學報,2015,22(5):98-102.

(編校：曾福庚)

Application of Genetic Algorithm and SimulatedAnnealing Algorithm in Multiple DNA Sequences

YAN Lei, MA Jian, DONG Hui, GAO Meng

(Department of Information Engineering, Bozhou Vocational and Technical College, Bozhou Anhui 236800, China)

The goal of sequence alignment—the alignment of genes or amino acids in proteins—is to uncover the similarity of two sequences.However, multiple sequence alignment is the comparison between multiple DNA sequences or protein sequences in order to discover the optimal comparing between the sequences groups.In the current study, genetic algorithm and simulated annealing methods were used to optimize the population concept by genetic algorithm.With the generation evolution, the approximate optimal solution was gradually generated.The experimental results show that the combination of genetic algorithm and simulated annealing methods enables the genetic algorithm to have more space to move when the local optimal solution is obtained, and the simulated annealing method can effectively solve the genetic algorithm for the bad regions.The combination of the two algorithms is better than the results of any single algorithm, so it can improve the overall alignment effect and will provide the biologist with appropriate help in judging the unknown sequence function in the future.

sequence alignment; multiple sequence alignment; genetic algorithm; simulated annealing method

格式：閆磊,馬健,董輝,等.基于遺傳算法與模擬退火算法在多重DNA序列比對中的應用研究[J].海南熱帶海洋學院學報,2017，24(2)：64-69.

2017-02-15

安徽省教育廳自然科學研究重點課題(KJ2016A493);安徽省亳州市產業創新團隊科研項目(亳組[2015]20號-2);亳州職業技術學院院級課題 (BYK1511)

閆磊(1984-),男,回族,安徽亳州人,亳州職業技術學院信息工程系助教,研究方向為數據挖掘、人工智能方向.

TP18

A

2096-3122(2017) 02-0064-06

10.13307/j.issn.2096-3122.2017.02.13