高中數學師生互動式教學現存問題及對策研究

虞羅錢

[摘 要] 互動是高效課堂的基本組成，本文從高中數學師生互動式教學的概念出發，分析了當前師生互動式教學所存在的問題，并提出優化策略.

[關鍵詞] 高中數學；師生互動式教學；存在問題；優化策略

高效的課堂離不開充分的互動，那么高中數學課堂的師生互動式教學是怎樣的？我們當前的互動式教學存在怎樣的問題？如何對此進行優化？以下是筆者的思考.

[?] 高中數學師生互動式教學的概念

所謂“師生互動式教學”，就是在教學過程中，學生通過師生間的相互協作與交流來實現認知的建構和能力的提升.該教學模式下，教師在課堂上，積極引導學生進行溝通和交流，由此強化學生的學習興趣，提升學生對教學活動的參與程度，進而實現教學效率的顯著提升.

高中數學有著龐大而復雜的體系，很多問題的處理不僅涉及數學知識的運用，還將涉及數學技巧和思維方法的運用. 因此教學過程中，學生不能僅僅只是被動地聽講，而應該以積極主動的姿態參與進課堂研討，通過和老師、同學之間積極地互動來維持思維的活躍程度，從而掌握方法、習得知識.

[?] 高中數學師生互動式教學的存在問題

新課改不斷推進的過程中，高中數學教學的很多問題被暴露出來，其核心就在于如何有效地促進師生互動的進行，具體表現為互動過程中學生的體驗被忽略、學生主體意識較為模糊、師生互動效果的評價機制缺失等問題.

1. 互動過程中學生的體驗被忽略

學生數學能力的發展離不開教師有效的引導，那么教師在教學活動中是否肩負起自己的責任了呢？是不是每一個學生都有機會成為教學互動積極的參與者. 事實上，二者之間經常呈現為不對稱的關系，具體的表現是教師受傳統師生觀念的束縛，經常自發地將自己定位為課堂的“主體”或者“主演”，他們很少關注“客體”的真實體驗，甚至部分“客體”都無法找到自己課堂互動過程中的存在感.被忽略的“客體”也會逐步接受自己的身份定位，他們也將逐漸適應被忽略的情形，由此他們也將忽略教師的存在，最終的結果是課堂上，教師與學生各自為政、互不打擾、相安無事，這樣的課堂自然也就談不上什么互動教學.

2. 學生主體意識較為模糊

誰是數學課堂的主體？這是一個值得商榷的問題，現實情況下，教師往往會將學生帶進誤區：即教師是教的主體，學生是學的主體. 這種說法在一定層面上是正確的，但是如果用這一思維來進行灌輸式教學，就可能割裂教與學之間的關系，很大程度上抹殺了學生主動學習、積極思考的主體意識，其結果是教師被動地教，學生被動地學. 而在倡導互動教學的課堂上，學生和教師應該不斷地在變換著主客體的角色. 例如，長期占據主體地位的教師應該創造更多的機會，讓學生以主人翁姿態來參與教學，對于具體的數學問題，發表自己的認識和觀點，從而真正體現互動活動的雙向性，進而提升互動的效率.

3. 師生互動效果的評價機制不健全

有效的課堂互動離不開正確的認識、準確的定位、科學的方法，也離不開合理的評價機制. 互動效果如何直接決定著數學課堂的發展方向. 這不僅需要定性的評價，也需要定量的評價，它需要進行細化和量化的分析. 例如，通過問卷調查或訪談，了解學生通過互動能否獲得發展.而現在的情況是，教師定性判斷互動效果的依據是課堂表面上的氛圍，他們誤解為課堂熱鬧、氛圍活躍就是師生互動有效性的體現，定量評價的依據則是考試，考試成績優秀就可據此評價互動效果較好，反之則互動效果較差. 這顯然偏離了素質教育的主旨，應該在教學中予以糾正.

[?] 高中數學師生互動式教學的優化策略

分析當前數學課堂上師生互動所存在的問題，筆者認為可以從以下幾個方面著手，改進我們的教學.

1. 設置任務，豐富學生的體驗

如何增加學生的學習過程體驗呢？筆者認為，我們的教學不應該是知識的灌輸與填塞，而應該設置具體的任務，將知識學習碎片化、過程化.

如，分段函數的教學，可以設置如下幾個任務.

任務1：已知函數y=x，y=，y=x2，請你以這三個函數為“原材料”構造分段函數.

任務2：已知函數y=x，y=，y=-，y=x2，請你以這四個函數為“原材料”構造出單調遞增的分段函數.

任務3：已知函數y=x，y=-x，y=，y= -，y=x2，y=-x2，請你以這六個函數為“原材料”構造出具有奇偶性的分段函數.

設計意圖與點評：在分段函數的教學上，筆者通過“構造”這一思維活動讓學生自主探究，呈現學生對分段函數的原有認知，增強學生的過程體驗，同時這個過程又是有師生互動的參與的，從任務1到任務3，原材料不斷增加繼而不斷地豐富分段函數的類型，學生在完成任務的過程中有自己獨立的思考，也有與他人的合作交流，最終能夠歸納出分段函數的各種性質、特點，學生在這個過程中不僅僅學會了知識，同時整個課堂呈現百家爭鳴的學術研究味.

2. 開放設問，發散學生的思維

學生是教學的主體，學生的思維如何反映在對同一個問題的思考角度、廣度上. 為此，筆者認為，設置具有開放性的問題，讓學生獨立思考，不僅僅可以有效發散學生的思維，還可以將學生的思考結果作為課堂教學的新的生長點，由此開啟互動探究的新征程.

例如，設某二次曲線經過點A（1，2）和點B（0，3），請寫出該曲線的函數方程.二次曲線涵蓋圓、橢圓、拋物線和雙曲線，而且只限定兩個點，因此無論哪一類曲線都可能有無數組解，這大大提升了問題的靈活性，學生可以從自己的角度給出很多答案，這樣的問題不僅將促成學生對圓錐曲線的綜合性理解，也將有效挖掘學生的互動潛力.

當然，發散與集中是相對的，我們在教學過程中，開放性設問可以集中對于同一個知識點進行，采用變式訓練或進一步追問的方式，有效發散學生的思維，同時又可以聚合學生對同一個知識、概念的深入理解.

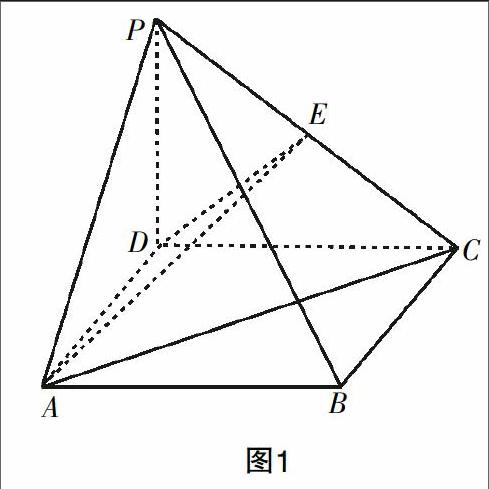
例如，立體幾何的學習過程中，有這樣一道題.

如圖1所示，四棱錐P-ABCD中，底面ABCD為矩形，PD⊥面ABCD，PD=DC=4，AD=2，E為PC中點，求證：AD⊥PC.

學生在這個問題解決后，如何引導學生的思維向更深處發展呢？我們可以以此為基礎進一步追問.

追問1：三棱錐P-ADE的體積是多少呢？

這個問題與前面的例題相比顯然需要學生有更深入的思考，在追問1解決后，還可以視具體的學情，可以二次追問.

追問2：在線段AC上是否存在一點M，使得PA∥平面EDM，若存在，求出AM的長；若不存在，請說明理由.

與追問1相比，追問2又一次將學生的思維引向深處，學習數學知識的過程是漸進式發展的過程，設置有梯度的提問是教師主導性作用發揮的表現，學生在思考問題的過程中會遇到困難，這些困難又可以作為合作探究的重要資源，最終隨著問題設置的深入，學生對知識、方法的認識越來越清晰、深刻，思維也隨著解決問題的過程逐步走向深入.

3. 總結評價，提升學生數學學習的情感

互動式教學不僅僅只有教與學，還應該在恰當的時候有總結與評價.

（1）在學生獲得階段性研究成果時，要及時地予以鼓勵，“很好！”“這個思路很正確！”“繼續往下思考，你看看還有什么新的發現”等等.

（2）當學生學習過程中遇到困難時，首先要肯定他的努力，幫助其發現出現困難的原因，及時幫助他總結經驗和教訓，引導其走上正確的探究方向.

（3）在知識點和方法學生討論、交流完成后，我們教師還要進一步總結提煉一下，幫助學生形成正確、完整的認識.

教育的最終價值在于：喚醒人的生命感、價值感和創造感，正如雕塑藝術家羅丹告訴我們：“所謂大師，就是這樣的人，他們用自己的眼睛看別人看過的東西，在別人司空見慣的東西上發現出美來.”只有有了獨特的感受和發現，才可以算是真正把握了美. 我想這也正是對教學美提升課堂教學有效性的最好診釋.引導學生充分地互動獲得知識的過程是學生的主觀能動性得到發揮的過程，通過問題的設計讓學生自己去研究問題，獲得對知識的再發現，這本身就是獲取知識的心路歷程，要讓學生知曉探究知識的過程是艱辛的，而我們教師在學生學習的心路歷程中，時不時地給予鼓勵和幫助，會讓學生的學習更具方向性，更能讓其振奮而充滿信心.