一道立體幾何題的思考

佛山市實驗中學(528061) 謝偉帆

一道立體幾何題的思考

佛山市實驗中學(528061) 謝偉帆

1 試題呈現

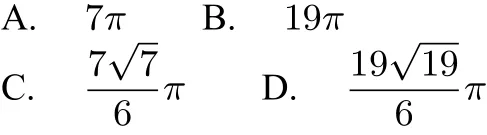
2 試題分析

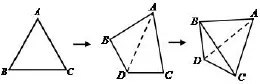
圖1

3 漸入誤區

由于割補法可以使問題簡單化,學生在思考的時候第一個想法是將四面體補成四棱柱,球的直徑為四棱柱的對角線長,如圖2所示.

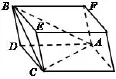
圖2

4 錯因分析

總結:外接球問題可以補成棱柱必須滿足兩個條件:(1)底面對角互補(2)側棱垂直底面.結合本題,若∠BDC=120°,則可補成四棱柱.

5 正解發現

此題的正確解法是怎樣呢?經過思考,學生提出了自己的想法.

法一:學生A提出用向量的方法解決,因為AD⊥面BCD,這樣給建立空間直角坐標系提供了方便,這種方法固然可行,但運算量較大.

法二:學生B是這樣考慮的,∠ADC=90°,取AC中點為F,則點F到點A,D,C的距離相等.如圖3,作面ADC的垂線FG,由勾股定理知點G到點A,D,C的距離相等,只需使BG=AG,則G為外接球球心.

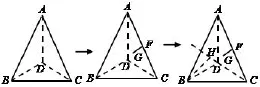
圖3

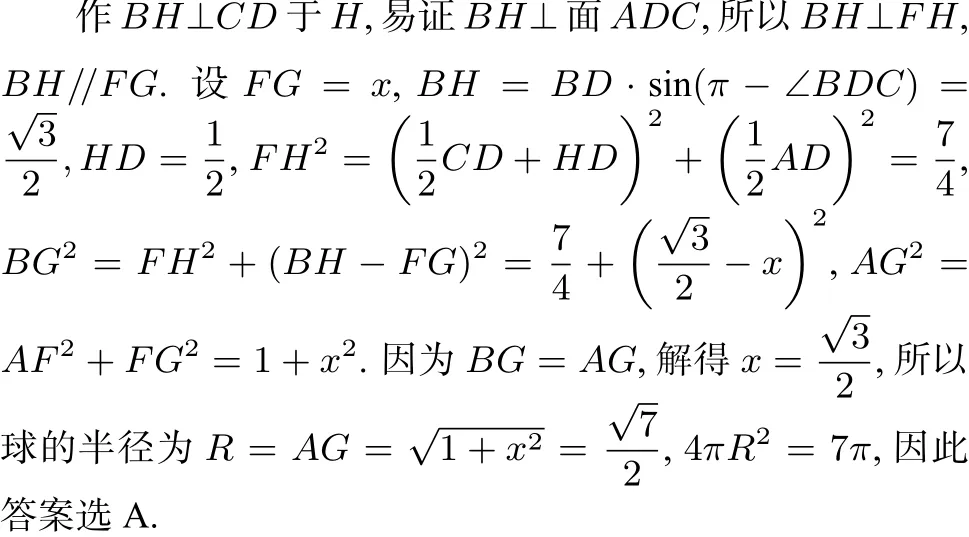
總結:法二利用直角三角形找出到三個頂點距離相等的點F,通過面的垂線,使得到第四個點的距離與之前的距離相等,從而確定球心和半徑.此方法要求有較強的空間想象能力及運算能力.

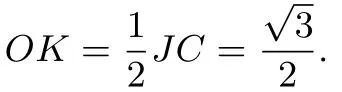
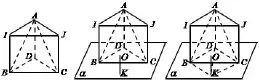
圖4

結合學生B的想法,O是球心,K∈α,OK⊥α,所以K到B,D,C的距離相等.因為BD=CD=1,∠BDC=120°,因此K恰好是以BD,CD為鄰邊的平

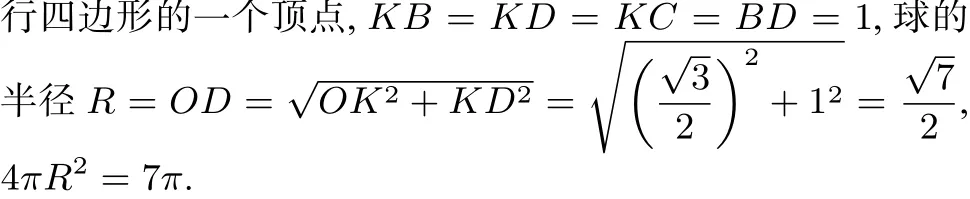
總結:法三利用了直三棱柱外接球的性質:球心到底面的距離等于側棱的一半,結合了法二,直接計算出球的半徑.此法非常巧妙,融合了割補法、代數的思想,是數形結合思想很好的體現.

6 總結反思

利用了幾何性質往往能更直觀地揭示隱藏的關系,使得運算簡便,這是純代數方法所不具備的,也是數形結合妙處所在.