夯實(shí)基礎(chǔ) 穩(wěn)步提升—由一節(jié)“一次函數(shù)復(fù)習(xí)課”引發(fā)的思考

廣東省廣州市礦泉中學(xué)(510400) 黃粵華

夯實(shí)基礎(chǔ) 穩(wěn)步提升—由一節(jié)“一次函數(shù)復(fù)習(xí)課”引發(fā)的思考

廣東省廣州市礦泉中學(xué)(510400) 黃粵華

一、教學(xué)背景

復(fù)習(xí)課是根據(jù)學(xué)生的認(rèn)知特點(diǎn)和規(guī)律,在學(xué)習(xí)的某一個(gè)階段,以鞏固、梳理已學(xué)知識(shí)、技能,促進(jìn)知識(shí)系統(tǒng)化,提高學(xué)生運(yùn)用所學(xué)知識(shí)解決問題的能力為主要任務(wù)的一種課型.其目的是溫故知新、查漏補(bǔ)缺,完善認(rèn)知結(jié)構(gòu),促進(jìn)學(xué)生解題思想方法的形成,發(fā)展數(shù)學(xué)能力.

就一個(gè)單元的復(fù)習(xí)而言,往往不是一節(jié)課可以完成的.從復(fù)習(xí)課的設(shè)計(jì)來看,可以是零散知識(shí)點(diǎn)的系統(tǒng)化整合,可以是專項(xiàng)題型的技巧訓(xùn)練、思維訓(xùn)練,也可以是某一個(gè)知識(shí)領(lǐng)域的拓展探究等,這些都有別于新授課.如何在較短的時(shí)間內(nèi),將零散的、點(diǎn)狀的基礎(chǔ)知識(shí)點(diǎn)整合好、系統(tǒng)化,同時(shí)又要將學(xué)生平時(shí)所學(xué)知識(shí)的疑惑點(diǎn)加以澄清,對(duì)所學(xué)知識(shí)的重要思想方法加以提煉,需要教師在復(fù)習(xí)課的設(shè)計(jì)和實(shí)踐中加以研究.本文試著從一堂一次函數(shù)的復(fù)習(xí)課入手,談?wù)勗诨A(chǔ)知識(shí)點(diǎn)的復(fù)習(xí)當(dāng)中如何幫助學(xué)生整理知識(shí)結(jié)構(gòu),構(gòu)建知識(shí)體系,提高復(fù)習(xí)效率.

二、教學(xué)設(shè)計(jì)與實(shí)施過程

活動(dòng)1: 以題點(diǎn)知,溫故知新

環(huán)節(jié)1: 下列函數(shù)中,哪些y是x的一次函數(shù),哪些y是x的正比例次函數(shù):

生2: 第(1)和(4)都是一次函數(shù),因?yàn)檎壤瘮?shù)也是一次函數(shù).

師: 能說說兩者之間的關(guān)系嗎?

生3: 一次函數(shù)解析式是y=kx+b(k/=0)的形式,當(dāng)b=0時(shí),即化為正比例函數(shù)的形式,所以正比例函數(shù)是一次函數(shù)的特殊形式,但一次函數(shù)不一定是正比例函數(shù).

環(huán)節(jié)2: 填空(1).正比例函數(shù)y=2x的圖象經(jīng)過第___象限,過點(diǎn)(0,___)與點(diǎn)(1,____),y隨x的增大而___.(2).一次函數(shù)y=x+2的圖象經(jīng)過第___象限,圖像與x軸的交點(diǎn)坐標(biāo)是___,與y軸的交點(diǎn)坐標(biāo)是____,y隨x的增大而___.

生4: 函數(shù)y=2x的圖象經(jīng)過第一、三象限,過點(diǎn)(0,0)和點(diǎn)(1,2),y隨x的增大而增大.

生5: 函數(shù)y=x+2的圖象經(jīng)過第一、二、三象限,與x軸的交點(diǎn)坐標(biāo)是(-2,0),與y軸的交點(diǎn)坐標(biāo)是(0,2),y隨x的增大而增大.

師: 能不能結(jié)合圖形進(jìn)行歸納說明?

生6: 板書畫圖說明兩個(gè)函數(shù)的k值都是大于零的,所以直線從左往右上升,即y隨著x增大而增大.正比例函數(shù)b值為零,所以直線經(jīng)過原點(diǎn),一次函數(shù)與y軸交點(diǎn)坐標(biāo)為(0,b).

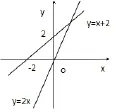
圖1

環(huán)節(jié)3: 拓展研究,知識(shí)延伸

師: 能不能求這兩條直線的交點(diǎn)坐標(biāo).

生7: 可以,如果作圖標(biāo)準(zhǔn),可以直接從圖像上得出,也可以解方程組

師: 在此坐標(biāo)系中是否存在與直線y=x+2沒有交點(diǎn)的直線,如果有,需要滿足什么要求,并請(qǐng)舉例.

生8: k值相同的直線與直線y=x+2沒有交點(diǎn),因?yàn)榇藭r(shí)兩條直線平行,如直線y=x+1,直線y=x-2等.

師: 什么時(shí)候兩個(gè)函數(shù)的值是一樣?

生9: 兩直線的交點(diǎn)就是函數(shù)值相等的時(shí)候,也就是方程組的解,即當(dāng)x=2時(shí),y=4.

師: 除了在點(diǎn)(2,4)相同以外呢?

生10: 從圖像上看,當(dāng)x＜2的時(shí)候,在點(diǎn)(2,4)的左邊,函數(shù)y=x+2的圖像在上方,此時(shí)y=x+2的函數(shù)值較大,也可以解不等式x+2＞2x;反之則是函數(shù)y=2x的圖像在上方.

【設(shè)計(jì)意圖】通過兩組小題進(jìn)行對(duì)比練習(xí),復(fù)習(xí)一次函數(shù)和正比例函數(shù)的概念,總結(jié)函數(shù)的圖像和性質(zhì),以及函數(shù)與坐標(biāo)軸的交點(diǎn)坐標(biāo),理解直線平行的要求,理解函數(shù)與方程、不等式之間的關(guān)系.

活動(dòng)2: 抓住核心,掌握基本方法

例題1已知一個(gè)一次函數(shù)經(jīng)過點(diǎn)(3,5)和(-4,-9),求這個(gè)函數(shù)的解析式.

變式1: 已知一個(gè)一次函數(shù),當(dāng)自變量x=3時(shí),函數(shù)值y=5;當(dāng)x=-4時(shí),y=-9,求這個(gè)函數(shù)的解析式.

變式2: 已知一個(gè)一次函數(shù)經(jīng)過點(diǎn)(3,5),且平行于直線y=2x+3,求這個(gè)函數(shù)的解析式.

變式3: 已知一個(gè)一次函數(shù)經(jīng)過點(diǎn)(3,5),且與y軸相交于點(diǎn)A,OA=1,求這個(gè)函數(shù)的解析式.

變式4: 已知一個(gè)一次函數(shù)平行于直線y=2x+3,且與y軸相交于點(diǎn)A,OA=1,求這個(gè)函數(shù)的解析式.

生11: 變式1和原題其實(shí)是一樣的,都給出了兩個(gè)點(diǎn)的信息,列方程組求出k值和b值就可以得到解析式了.

師: 是的,這就是本單元中非常重要的解析式求法,即待定系數(shù)法.

生12: 那其實(shí)變式2比變式1更易求解,表面上看題目只給了一個(gè)點(diǎn),但是已知兩直線平行,則k值是一樣的,所以只剩b值待定.

關(guān)于變式3和4,學(xué)生們展開了熱烈的交流,有很大一部分學(xué)生一開始都忽略了對(duì)“OA=1”的分析,通常都認(rèn)為點(diǎn)A即(0,1).

生13: 變式3中的條件“OA=1”說明點(diǎn)A與原點(diǎn)相距1個(gè)單位長度,它的坐標(biāo)可能是(0,1)或者是(0,-1),應(yīng)該有兩個(gè)解析式.

生14: 變式4也要進(jìn)行分類討論,而且還由平行知道k值是2.

生15: 看來,分類討論題也不是那么難.

【設(shè)計(jì)意圖】以求一次函數(shù)解析式這一典型問題為載體,展開變式訓(xùn)練,拉近點(diǎn)狀知識(shí)間的距離,尋找不同問題之間的內(nèi)在聯(lián)系,鞏固“待定系數(shù)法求一次函數(shù)解析式”,提升復(fù)習(xí)效率.

活動(dòng)3: 一題多變,發(fā)散思維空間

例題2 如圖,直線l1的解析表達(dá)式為y=-3x+3,且l1與x軸交于點(diǎn)D,直線l2經(jīng)過點(diǎn)A,B,直線l1,l2交于點(diǎn)C．

(1)求點(diǎn)D的坐標(biāo);

(2)求直線l2的解析式及C點(diǎn)坐標(biāo);

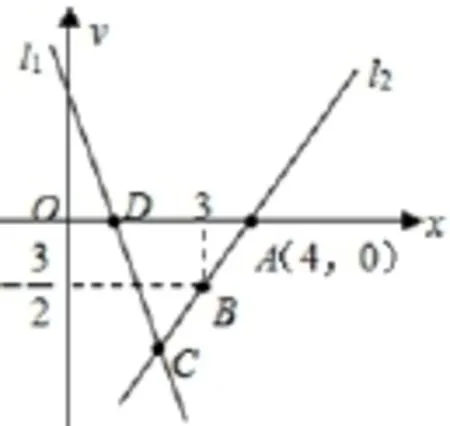
圖2

(3)求△ADC的面積;

(4)在直線l2上存在異于點(diǎn)C的另一點(diǎn)P,使得△ADP與△ADC的面積相等,請(qǐng)求出點(diǎn)P的坐標(biāo)．

(5)在直角坐標(biāo)系中有點(diǎn)E,和A,C,D構(gòu)成平行四邊形,請(qǐng)直接寫出E點(diǎn)的坐標(biāo)．

生16: 因?yàn)镈點(diǎn)落在x軸上,所以它的縱坐標(biāo)為0,將0帶入l1可以求得坐標(biāo)(1,0).

生17: 從圖像可以發(fā)現(xiàn)l2其實(shí)經(jīng)過了兩個(gè)點(diǎn),分別是A(4,0)和B(3,-1.5).

生18: 那△ADC的面積也很容易求的,用方程組可以先求交點(diǎn)C的坐標(biāo),然后縱坐標(biāo)的絕對(duì)值是高,線段AD做底.

師: 很好,看來同學(xué)們掌握的都很不錯(cuò),有進(jìn)步!那我們再來看看變式4的問題.

生19: 存在,△ADP與△ADC有公共邊AD,只要P點(diǎn)到x軸的距離等于C點(diǎn)到x軸的距離就可以了,所以P點(diǎn)的縱坐標(biāo)和C點(diǎn)的縱坐標(biāo)互為相反數(shù).

因?yàn)榍懊孢M(jìn)行了多個(gè)知識(shí)點(diǎn)的復(fù)習(xí),所以學(xué)生在問題(5)展開了激烈的討論,而且大部分的人一開始就猜想符合條件的E點(diǎn)不止一個(gè),學(xué)生們學(xué)習(xí)的熱情得到極大的提高.

生20: 當(dāng)CE平行且等于AD的時(shí)候,有平行四邊形,E點(diǎn)可以在C點(diǎn)左邊,也可以在右邊;還有一種可能是AE//DC,DE//AC,所以有三種可能.

【設(shè)計(jì)意圖】此例在一個(gè)圖形的背景下,做到問題的多變,將看似沒有關(guān)聯(lián)的知識(shí)點(diǎn)全部回歸至同一模型架構(gòu)之下進(jìn)行研究,所涉及的問題與本節(jié)課開篇首尾呼應(yīng),第(4)、(5)兩問加強(qiáng)了函數(shù)圖像與幾何圖形之間的聯(lián)系,凸顯數(shù)學(xué)模型思想.

三、教學(xué)思考

《數(shù)學(xué)課程標(biāo)準(zhǔn)(2011)版)》指出,數(shù)學(xué)課程要面向全體學(xué)生,人人都能獲得良好的數(shù)學(xué)教育,使不同的人在數(shù)學(xué)上得到不同的發(fā)展.由于現(xiàn)在各班學(xué)生的數(shù)學(xué)水平差異較大,根據(jù)課程標(biāo)準(zhǔn)的要求,在復(fù)習(xí)課的教學(xué)中,即要做到鞏固基礎(chǔ)知識(shí),查漏補(bǔ)缺,又要提升學(xué)生技能,發(fā)展思維,盡量縮小生與生之間的差異.

如果在復(fù)習(xí)課中占用大量時(shí)間采用背誦、默寫、齊讀等方式來對(duì)概念、公式、法則進(jìn)行重復(fù)和再現(xiàn),復(fù)習(xí)效率必然不高,也不利于學(xué)生對(duì)所學(xué)知識(shí)的再認(rèn)識(shí)和深入理解.在本節(jié)課中,筆者摒棄了傳統(tǒng)復(fù)習(xí)課教學(xué)中常見的“練習(xí)、練習(xí)、再練習(xí)”的模式,采取層層設(shè)問,師生互動(dòng)的形式,進(jìn)而引發(fā)學(xué)生主動(dòng)思考、歸納,逐步完成知識(shí)體系的重新構(gòu)建,優(yōu)化整合.

1.類比復(fù)習(xí),梳理知識(shí)結(jié)構(gòu)

學(xué)習(xí)一個(gè)由薄到厚,再由厚到薄的過程.一次函數(shù)的學(xué)習(xí)過程是由特殊到一般的過程,這其中涉及較多的概念、圖形性質(zhì)等方面的內(nèi)容.在新授課的過程中學(xué)生普遍認(rèn)為本章知識(shí)容量較大,學(xué)習(xí)起來往往顧此失彼.因此,在環(huán)節(jié)一中,通過幾組類似的練習(xí)題來復(fù)習(xí)正比例函數(shù)和一次函數(shù)概念、圖像性質(zhì)之間的練習(xí)和區(qū)別,采取老師問,學(xué)生答的形式,不斷進(jìn)行拓展和延伸,同時(shí)利用圖形進(jìn)行直觀對(duì)比,適時(shí)滲透數(shù)形結(jié)合思想,增加學(xué)生感性認(rèn)識(shí),幫助學(xué)生構(gòu)建完整知識(shí)架構(gòu),增強(qiáng)后繼復(fù)習(xí)的動(dòng)機(jī)和信心.

2.變式引領(lǐng),做到事半功倍

運(yùn)用變式題進(jìn)行教學(xué),是初中數(shù)學(xué)常用的一種教學(xué)手段,也是培養(yǎng)學(xué)生思維能力,提高應(yīng)變能力的一種有效方法.在教學(xué)過程中,恰當(dāng)使用好變式題,會(huì)使課堂教學(xué)取得事半功倍的效果.

在環(huán)節(jié)二中,一共有5個(gè)求一次函數(shù)解析式的問題,其中第1、2兩個(gè)問題的原型是教材中“用待定系數(shù)法求一次函數(shù)”例題模型,設(shè)計(jì)的目的就是定位于復(fù)習(xí)課要回歸教材,回歸基礎(chǔ),避免“題海戰(zhàn)術(shù)”.由于有了活動(dòng)一的鋪墊,在變式題的練習(xí)中,學(xué)生們都能較快的動(dòng)起來,甚至對(duì)于變式4這一類平時(shí)練習(xí)中較為困惑的內(nèi)容,也能積極參與想到解題思路和解題辦法,說明這種密臺(tái)階、低起點(diǎn)的復(fù)習(xí)設(shè)計(jì),在完成了基礎(chǔ)知識(shí)體系構(gòu)建的情況下,能夠達(dá)到較理想的復(fù)習(xí)效果.

3.由點(diǎn)及面,發(fā)展思維空間

英國國家數(shù)學(xué)課程強(qiáng)調(diào)開放性問題的作用,要求變封閉問題為開放問題.在數(shù)學(xué)教學(xué)中,只要把封閉問題加以改良,那就會(huì)使的教學(xué)變得更加有趣、富有挑戰(zhàn)性.在例3中雖然設(shè)計(jì)了多達(dá)5個(gè)問題,但是每一個(gè)都較為容易上手,學(xué)生在學(xué)習(xí)的的過程中能夠自然的體會(huì)到其中內(nèi)涵,在這種由淺入深、由易到難,循序漸進(jìn)的編排設(shè)計(jì)中,學(xué)生的復(fù)習(xí)效果會(huì)呈螺旋式遞進(jìn),同時(shí)原有的知識(shí)結(jié)構(gòu)也會(huì)在復(fù)習(xí)的過程中進(jìn)行優(yōu)化重組.猶如一間堆滿雜物的倉庫被重新整理擺放后一樣,遇到需求的時(shí)候要什么則拿什么,一個(gè)是效率的提升,另外這樣復(fù)習(xí)也能逐步深化學(xué)生對(duì)知識(shí)的理解,形成解題技巧,同時(shí)生成數(shù)學(xué)思維,發(fā)展數(shù)學(xué)思考能力.

[1]孔凡哲.新課程典型課案例與點(diǎn)評(píng).東北師范大學(xué)出版社.2003

[2]馬復(fù).設(shè)計(jì)合理的數(shù)學(xué)教學(xué).高等教育出版社.2003

[3]茅雅琳.“課堂讓學(xué)”理念下的課堂評(píng)析[J].中國數(shù)學(xué)教育(初中版), 2015(4): 33-36

[4]劉海濤.初三數(shù)學(xué)課堂針對(duì)學(xué)生差異的有效訓(xùn)練[J].中國數(shù)學(xué)教育(初中版),2015(6): 19-23

[5]張愛平.經(jīng)歷過程滲透思想發(fā)展能力[J].中國數(shù)學(xué)教育(初中版), 2015(6): 35-38

[6]陳文娣.加強(qiáng)數(shù)學(xué)思想引領(lǐng)注重教學(xué)過程優(yōu)化[J].中國數(shù)學(xué)教育(初中版),2015(6): 39-42