經濟數學教學中重要極限Ⅱ及其應用的信息化教學設計

趙薩日娜

（吉林省經濟管理干部學院，吉林長春 130000）

數學中常常會對一些重要且具有典型意義的問題進行研究并加以總結，以期通過對該問題的解決帶動一類相關問題的解決，兩個重要極限就體現了這樣的思路，利用它們并通過函數的恒等變形與極限的運算法則就可以使兩類常用的極限的計算問題得到解決。其中重要極限Ⅱ的形式及計算應用對學生來說更為復雜，難以掌握，且它在經濟數學問題——連續復利問題中有重要的應用。因此利用信息化教學法組織好重要極限Ⅱ及其應用的教學，對于訓練學生在動態變化的思維下理解極限過程的內在數量關系的能力，通過實際問題建立合理的抽象的數學模型的能力，以及按照目標模型進行靈活的恒等變形的能力都具有重要的意義。

1 教學背景

教學主體是經管類專業，如工商管理、財務管理專業大一新生,基本都是文科生，數學基礎相對薄弱,學習興趣有待提高。多數學生尚未養成自主學習習慣,掌握有效學習方法。學生的邏輯思維能力、恒等變形能力有待進一步開發和鍛煉。

對于學習本節課的相關知識基礎而言,基本了解指數函數的運算特點；理解函數極限的概念、無窮大和無窮小的概念；掌握了極限的運算律。

2 教學目標

3 教學重點

4 教學難點

5 教學方法

主要采用查表觀察和看圖觀察方法、利用MATLAB信息化教學法、講授法、數形結合法、啟發式教學法等。

6 教學內容

6.1 提出問題

假設本金數量為A的一項投資，以年利率R投資了n年，按復利付息，若每年計算一次復利，則

一年后的本利和為A1=A(1+R)；

二年后的本利和為A2＝A(1+R)；

年后的本利和為An＝A(1+R)n.

若一年分為m次付息，年利率仍為R，則每期利率為R/m，于是

這就是說一年計算次復利的本利和比一年計算一次本利和要大，且復利計算次數越頻繁,計算所得的本利和數額就越大，那么我們是不是可以計算無限次復利呢?

如果m→∞,則年后的本利和為

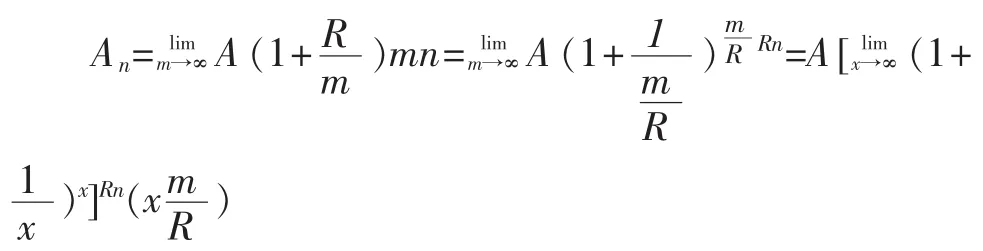
6.2 分析問題

按照當x→∞時函數極限的描述性定義及其幾何解釋,采用查表觀察和看圖觀察方法分析問題.

表1 計算器計算結果

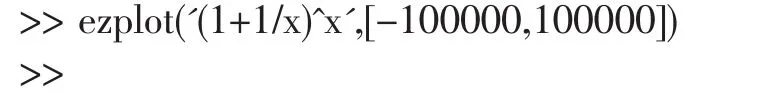
圖1 曲線圖形

6.3 解決問題

其中等式右端的數e是數學中的一個重要常數,其值為e＝2.718 281 828 459 045…,基本初等函數中的指數函數y＝ex以及自然對數函數y＝1nx中的底e就是這個常數。

至此,我們可以回答最初提出的問題,原來雖然復利計算次數越頻繁,計算所得的本利和數額就越大,但是也不會無限增大,因為

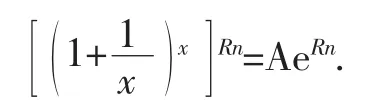
所以,本金為A，按名義年利率R不斷計算復利,則n年后的本利和為S＝AeRn。

上述公式稱為連續復利公式,式中的n可視為連續變量,上述公式僅是一個理論公式,在實際應用中并不使用它,僅作為存期較長情況下的一種近似估計。

6.4 應用舉例

（1）計算下列極限。

a.此極限為“1∞”型,也適合用來求此類極限；

因此，應用此重要極限的主要方法及步驟為：a.先判斷極限類型是否為1∞；b.恒等變形套模型;c.運用重要極限結果并結合函數運算律和極限運算律求出極限值。

（2）一投資者欲用1000元投資5年,設年利率為6%,試分別按單利、復利、每年按4次復利和連續復利方式計算，到第5年末，該投資者應得的本利和S。

解：按單利計算

S＝1000+1000×0.06×5＝1300（元）

按復利計算

S＝1000+（1+0.06）5＝1000×1.33823＝1338.23（元）

每年按4次復利

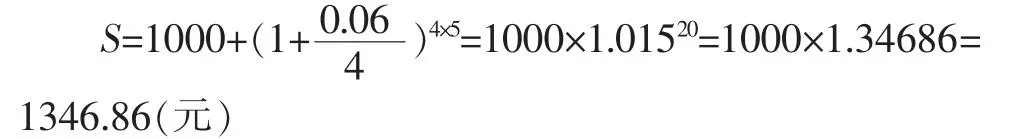
連續復利方式計算

S＝1000e0.06×5＝1000e0.3＝1349.86（元）

連續復利的計算公式在許多其它問題中也常有應用，如細胞分裂、樹木增長、放射性物質的衰減等。

[1]吳贛昌.大學文科數學[M].北京：中國人民大學出版社，2007.

[2]梁寶鈺.數學實驗[M].天津：南開大學出版社,2017.

[3]麥紅.Matlab在大學文科數學教學中的應用[J].電腦知識與技術,2008,4(35)：2272-2273，2285.