基于擴展目標先驗的貝葉斯壓縮感知成像
王天云, 劉冰, 叢波, 凌曉冬
(中國衛星海上測控部, 江蘇江陰 214431)
0 引言
近年來,高分辨率成像雷達因其在民用領域和軍用領域的巨大應用潛力,成為雷達領域的重要發展方向之一。其中值得一提的是,基于壓縮感知(Compressed Sensing, CS)理論的高分辨率成像技術因為在僅需較少的觀測樣本就能獲得非常高的成像效果,受到了國內外學者的廣泛關注。當前已有研究文獻利用目標自身的稀疏先驗信息,對CS成像方法(如貪婪算法、統計優化算法等)進行了廣泛而深入的研究[1-2]。
然而,上述成像方法在處理過程中通常基于如下前提——即目標自身的稀疏性非常好。考慮到實際情形中,尤其是大型剛體目標(如飛機、艦船等),其距離維及方位維通常存在擴展特性造成成像場景的散射點較多且呈區域性分布[3-5],此時目標空間域的稀疏性相對較差,因此直接應用傳統CS成像方法,會導致傳統稀疏重構方法的成像性能受限,尤其是在信噪比較低或者CS測量數目較少情形時,目標的形狀或輪廓信息不能得到較好的反演[6-7]。這是因為它們在目標稀疏重構的過程中沒有考慮擴展目標圖像的結構信息。
對擴展目標而言,成像區域除了散射點滿足稀疏性之外,還存在一些額外的先驗信息,比如目標連續區域邊界也滿足稀疏性等。這些因素在以往的CS成像方法[6-7]中均被忽略。因此如何有效地利用目標圖像的結構信息來進一步提高成像質量,并拓展已有的稀疏成像方法,是本文研究的重點。
基于此背景,本文在傳統目標稀疏先驗基礎上,進一步考慮利用擴展目標圖像的結構信息,在貝葉斯框架下利用目標場景連續性分布的先驗特性,提出基于擴展目標先驗分布的貝葉斯壓縮感知成像技術。具體做法如下:首先,對每個網格上目標散射點賦予伯努利-高斯(Bernoulli-Gaussian)先驗概率[8]以促進目標稀疏性;然后,根據散射點服從的不同的連續模式(即用來刻畫擴展目標圖像的連續特性)推導各參數服從的后驗概率估計;最后,再利用變分貝葉斯(Variational Bayesian, VB)[9]方法交替迭代求解,直至收斂,即能重構目標圖像。仿真結果驗證了所提方法的有效性,并展示在相同雷達系統配置模式下相比傳統稀疏重構方法的優勢。
1 信號模型
1.1 雷達成像模型簡介
眾所周知,在波恩弱散射近似條件下,雷達成像問題可以利用下述線性方程進行統一表征[10]:
y=Aσ+n
(1)

傳統稀疏重構方法一般是將式(1)轉化為如下優化問題的求解:
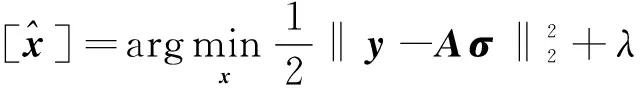
(2)
式中,φ(σ)可以為l1范數(如BP方法)[11]、lp范數(如FOCUSS方法)[12]約束等。
根據前面分析,對大型剛體目標進行成像時,其距離維及方位維通常存在一定的擴展特性,此時成像場景中的散射點較多且呈區域性分布,因此目標空間域的稀疏性將大大減弱,采用式(2)對應的傳統CS成像方法所能獲得的目標稀疏重構結果常常并不理想[7-8],這是因為它們在稀疏重構過程中沒有考慮擴展目標圖像的結構信息。
1.2 基于擴展目標先驗的貝葉斯壓縮感知成像
借鑒文獻[13]的思想,本文首先構建了如圖2所示的擴展目標稀疏貝葉斯先驗模型,具體描述如下。
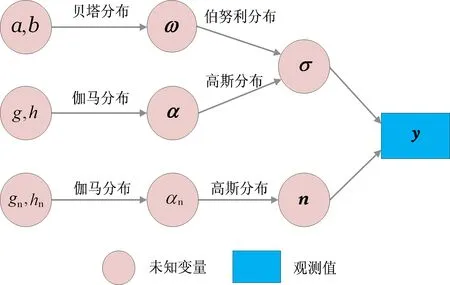
圖2 擴展目標稀疏貝葉斯先驗模型
1.2.1 目標稀疏先驗模型
p(σi|ωi,αi)=(1-ωi)δ(|σi|)+
(3)
式中,1≤i≤UV,ωi為伯努利分布的參數,服從貝塔分布(因為貝塔分布與伯努利分布成共軛先驗),即ωi~Beta(a,b),a,b是貝塔分布的參數,表達式為
(4)
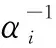
(5)
再假定各散射點的散射系數σi滿足獨立同分布,則目標散射系數矢量σ的概率分布為
(6)
1.2.2 噪聲模型
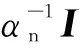
(7)
進一步,假定噪聲功率倒數αn服從參數為gn,hn的伽馬(Gamma)分布:
(8)
1.2.3 改進的貝葉斯壓縮感知成像算法
由圖2所示的擴展目標貝葉斯稀疏模型,利用基于最大后驗(Maximum A Posteriori, MAP)準則[14]得到回波矢量y的后驗概率分布:
p(σ,ω,α,αn|y)∝p(y|σ,αn)·
p(σ|ω,α)p(ω)p(α)p(αn)∝
(9)
根據之前賦予相關參數的先驗概率分布,通過式(9)可以直接計算出各隨機變量服從的后驗概率密度函數。
步驟1:σi的后驗概率為
p(σi|σ/σi,y,ω,α,αn)∝
式中,
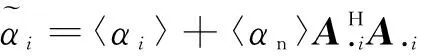
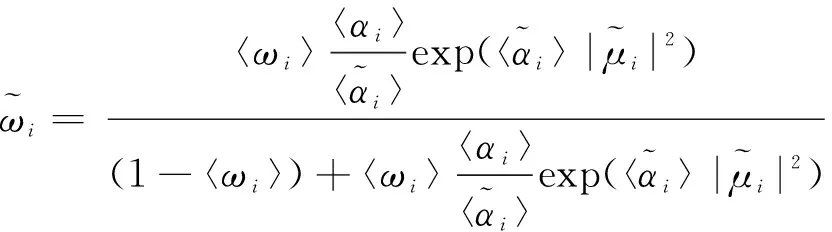
(11)
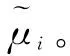
步驟2: 在求解αi的后驗概率時,文獻[13]考慮了3種可能的目標連續性模式,如圖3所示的model 1~model 3。本文將其推廣至6種可能的連續性模式,如圖3所示的model 1~model 6,其中圖中陰影方塊表示該處的散射系數值不為0,白色方塊表示該處的散射系數值為0。
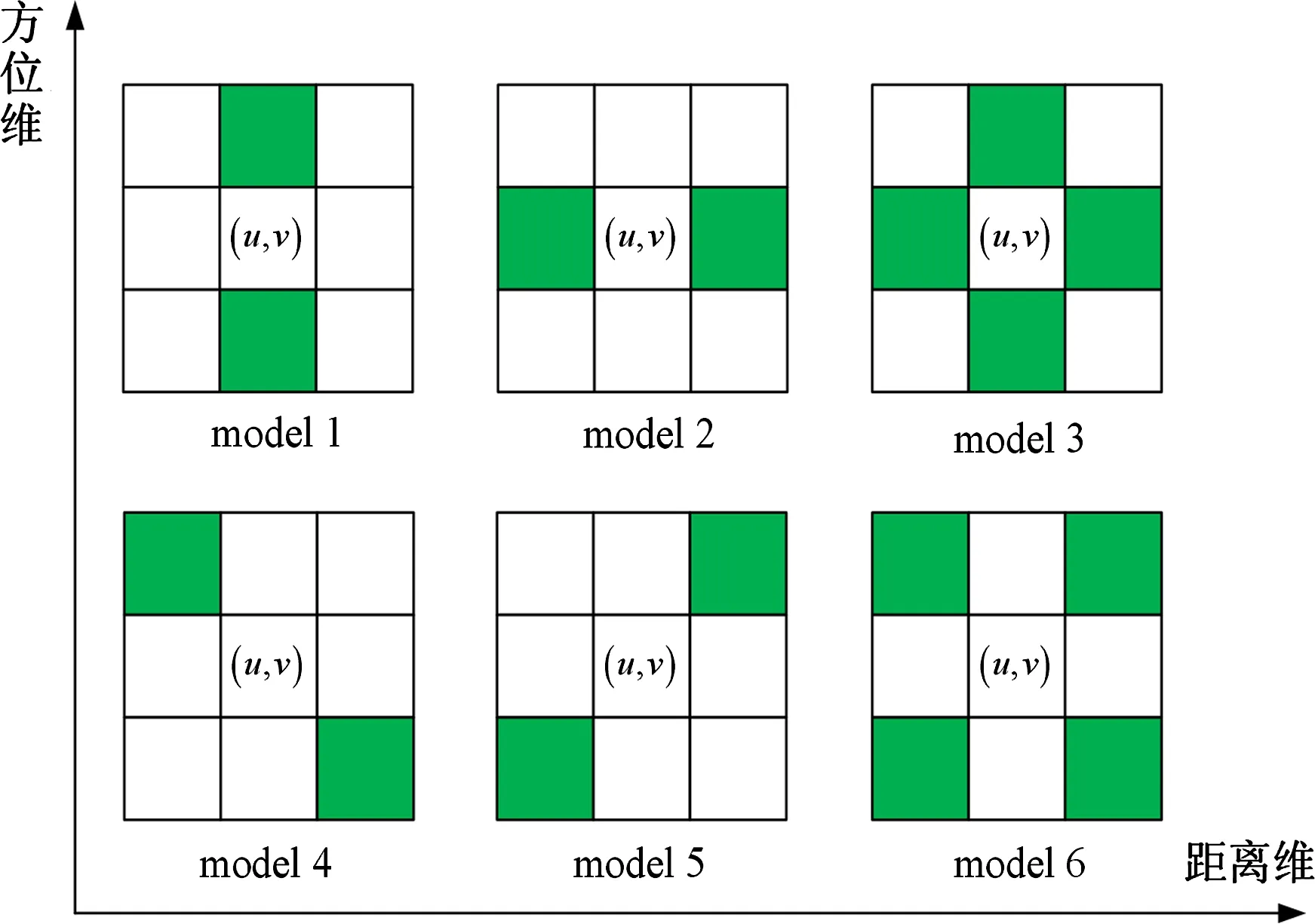
圖3 表征擴展目標散射點分布的6種連續模式
1) 若第i個散射點(即第(u,v)個網格)符合第3種連續模式,那么αi的后驗概率為
(12)
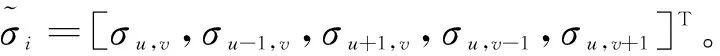
(13)
經推導,αi的均值為
(14)
2) 若第i個散射點滿足第1或第2種連續模式,那么αi的后驗概率為
(15)
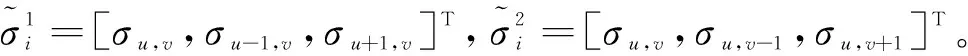
(16)
經推導,αi均值為
(17)
3) 若第i個散射點不滿足第1,2,3種連續模式但滿足第6種連續模式,那么αi的后驗概率為
(18)
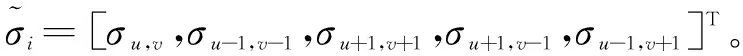
(19)
經推導,αi均值為
(20)
4) 若第i個散射點不滿足第1,2,3種連續模式但滿足第4或第5種連續模式,那么αi的后驗概率為
(21)
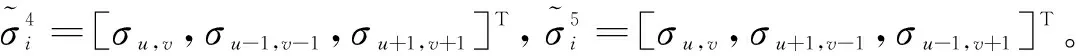
(22)
經推導,αi均值為
(23)
5) 若第i個散射點不滿足任意一種連續模式,類似地,得到αi的后驗概率為
(24)
經推導,αi均值為
(25)
步驟3: 在求解ωi的后驗概率時,與文獻[13]的做法類似,本文考慮了如下3種可能的稀疏模式:
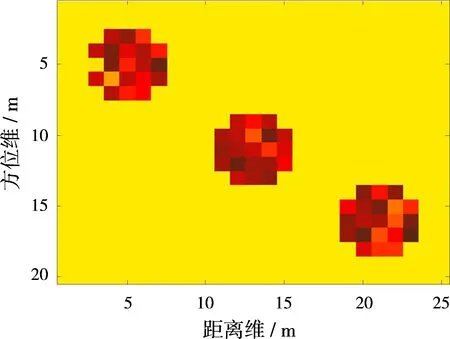
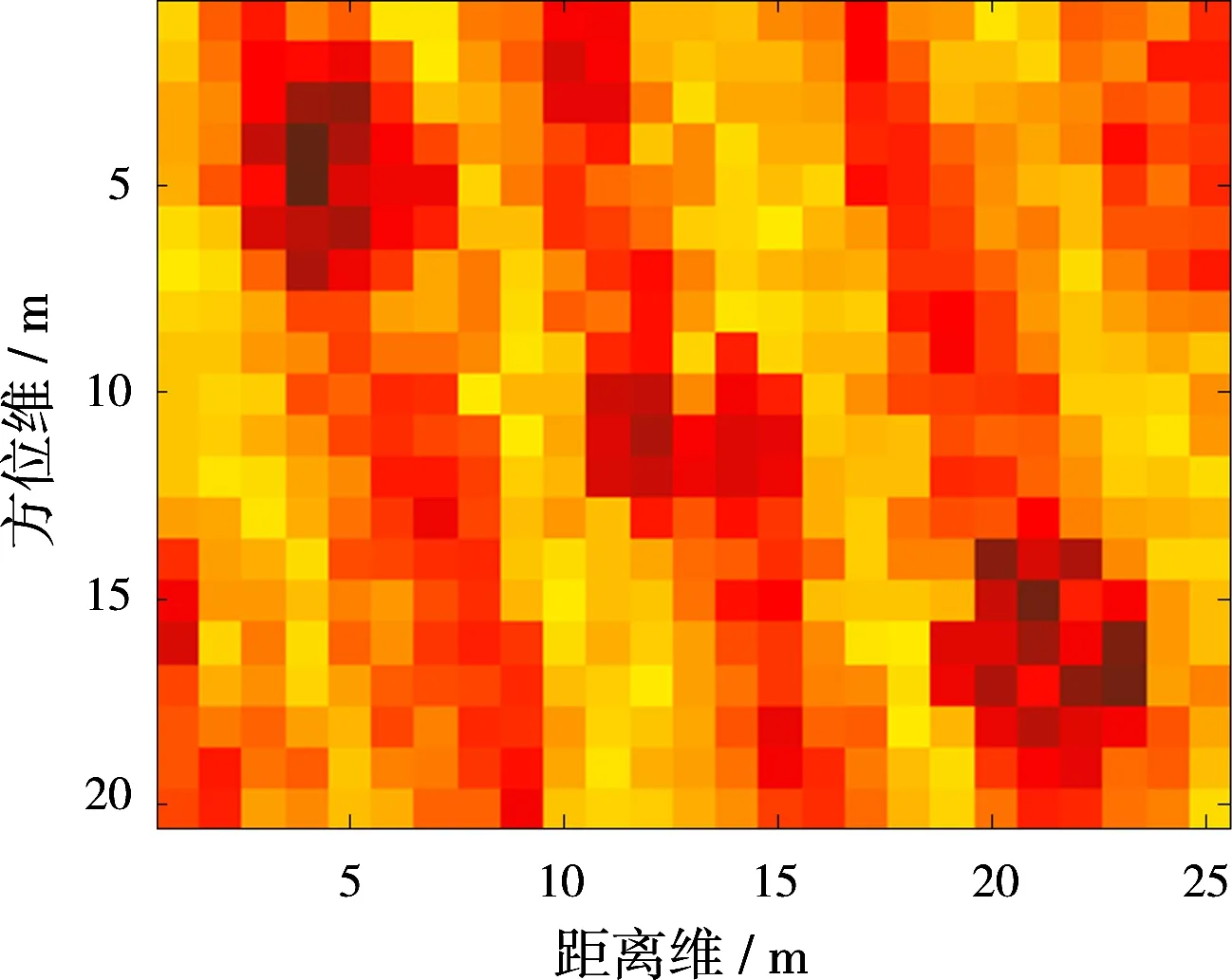
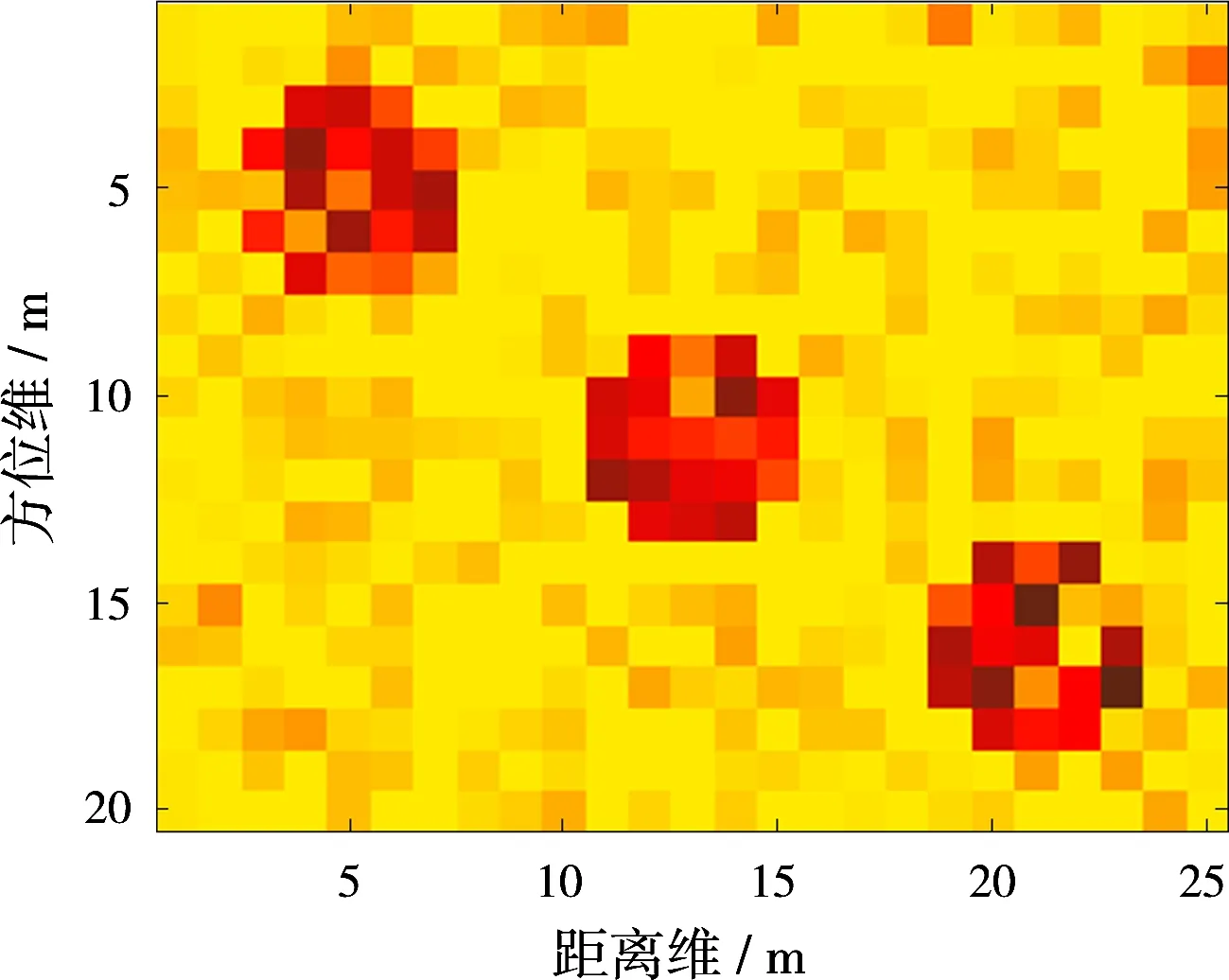
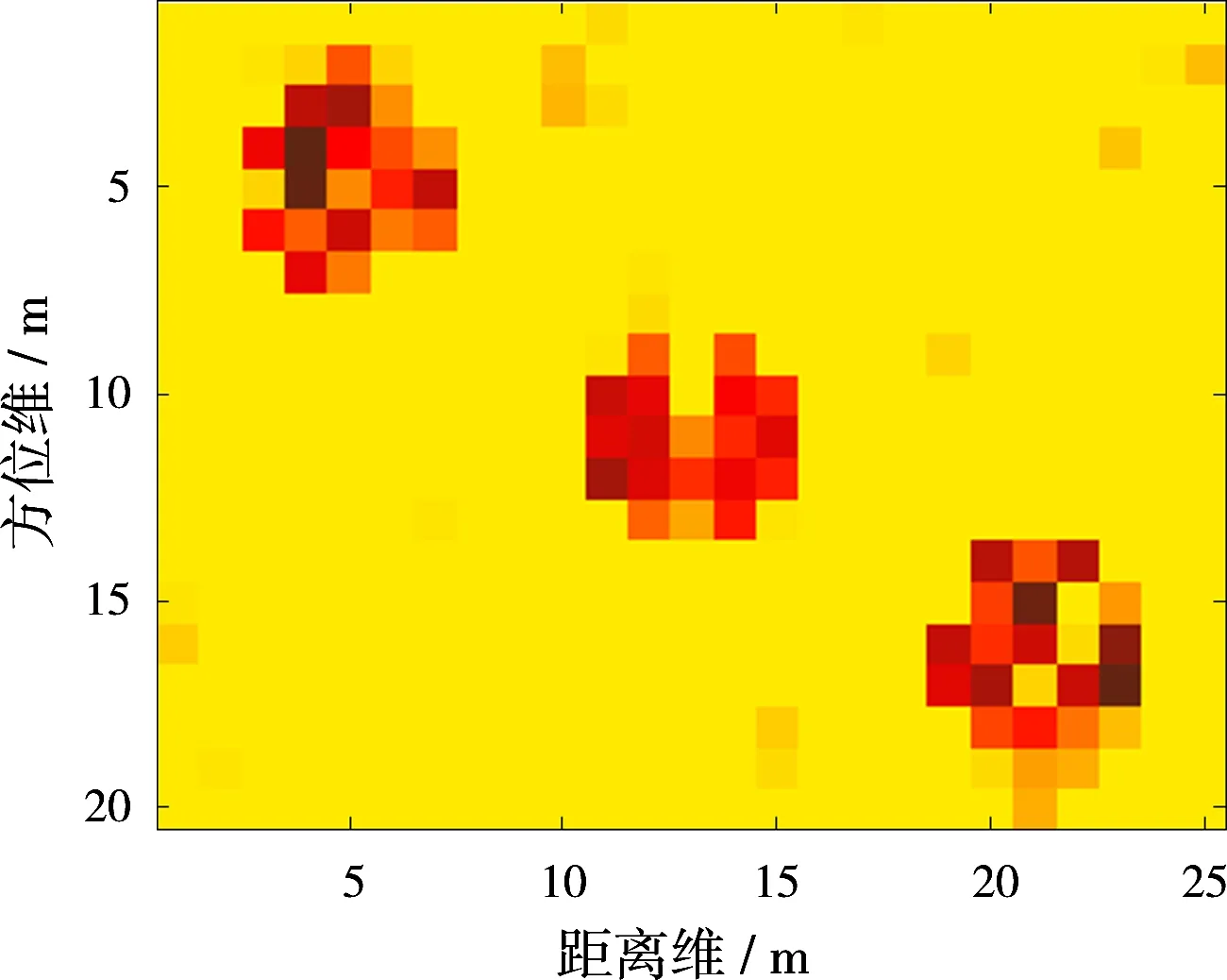
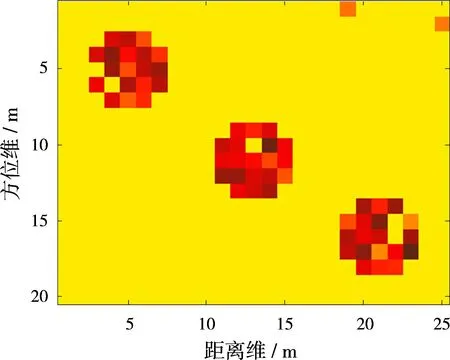
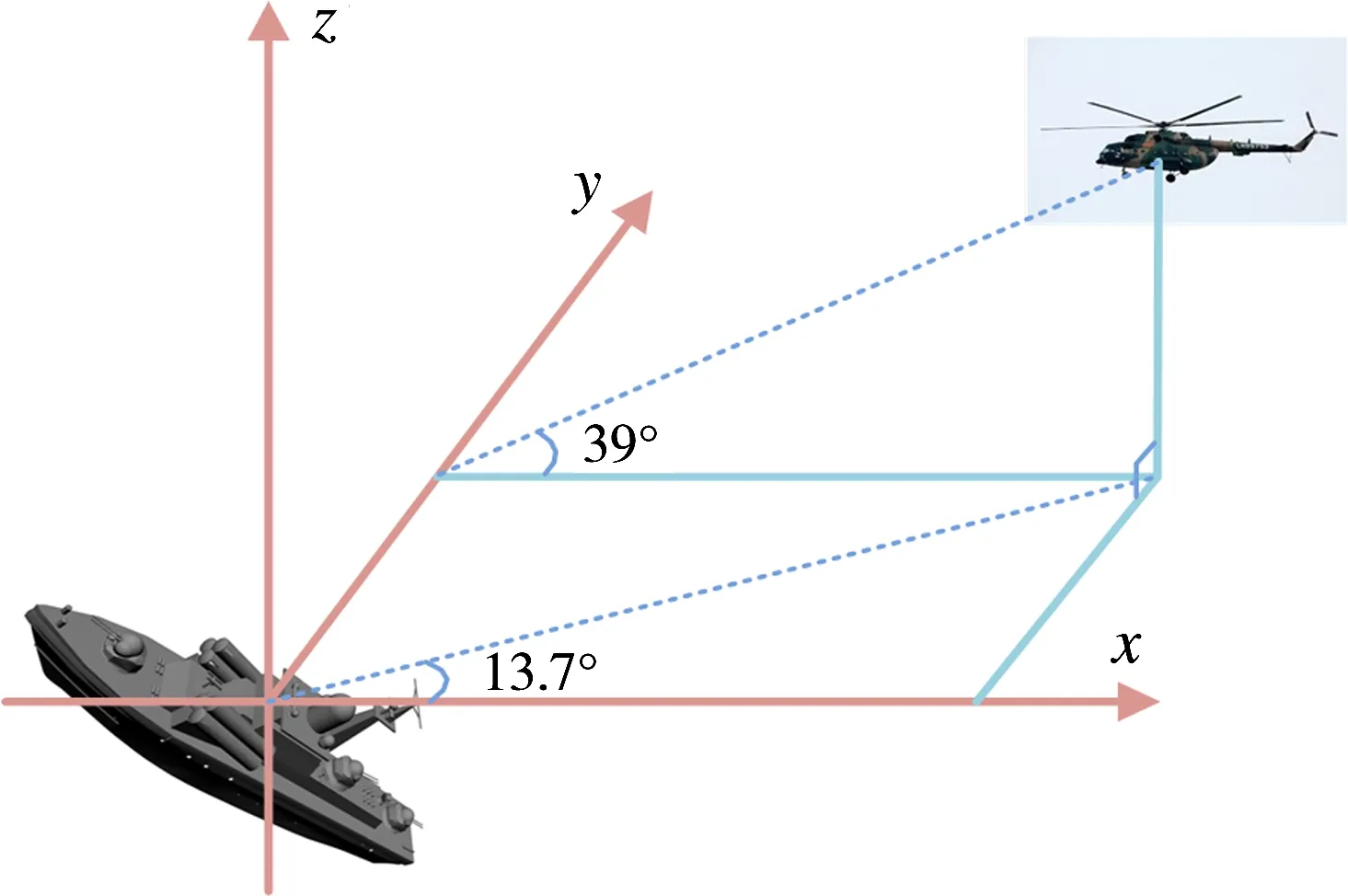
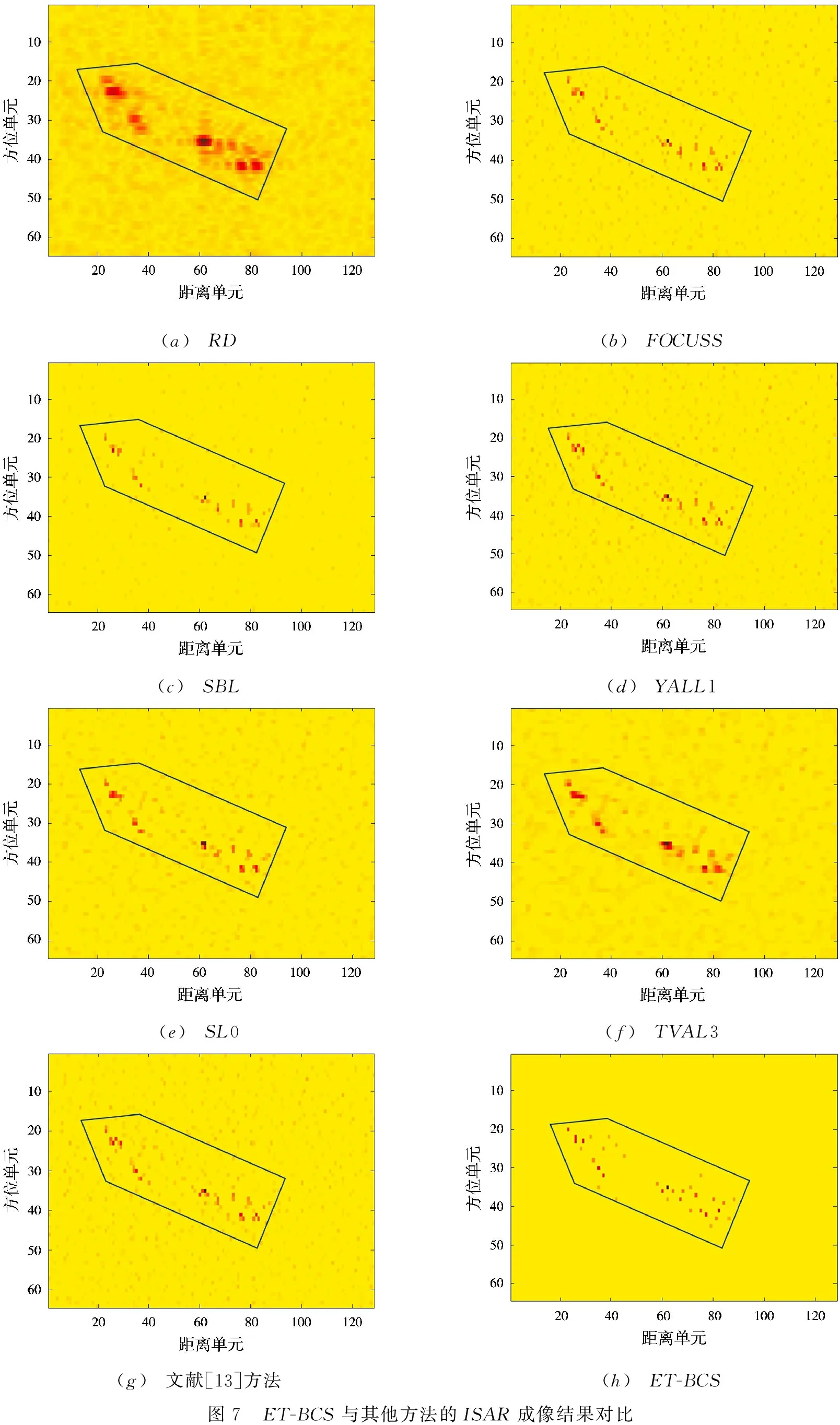
1) 稀疏模式1:第i個散射點周圍的點散射系數都為0,設置ωi先驗概率中的參數a,b滿足a0 2) 稀疏模式2:第i個散射點周圍的點滿足任意一種連續模式,設置ωi先驗概率中的參數a,b滿足a1>b1,此時ωi趨于1,即σi趨于非0。 3) 稀疏模式3:第i個散射點周圍的點不符合以上兩種情況,設置ωi先驗概率中的參數a,b滿足a2=b2;此時ωi趨于1/2,即σi取0或者非0的概率相等。 相應地,ωi的后驗概率為 (26) 可以看出,ωi的后驗概率是貝塔(Beta)分布的形式: (27) 根據式(27),得出ωi的均值為 (28) 步驟4: 最后求解噪聲功率倒數αn的后驗概率,經推導αn也服從伽馬(Gamma)分布: p(αn|σ,gn,hn)=Γ(αn|gn+M,hn+ (29) 根據式(29),得出αn的均值為 (30) 依據以上各隨機變量的后驗概率分布和相應的均值,本文采用VB方法求解式(9)對應的貝葉斯推斷問題,通過交替迭代求解各隨機變量的均值,直至收斂,即能準確重構目標圖像。與文獻[13]采用Gibbs求解方式相比,本文基于VB方法具有更高的參數提取精度,這可以通過后續的仿真結果對比看出。 綜上所述,基于擴展目標先驗分布的貝葉斯壓縮感知成像算法流程如下: 輸入:y,A,lmax; 初始化: ①g=h=gn=hn=10-6; ② (a0,b0)=(1/M,1-1/M), (a1,b1)=(1/M,1/M), (a2,b2)=(1-1/M,1/M); ③ 目標散射系數σ的初始估計:〈σ〉(0)=AHy; ④α的初始估計:〈α〉(0)=1/AHy; ⑤ω的初始估計:〈ω〉(0)=1; ⑥αn的初始估計:〈αn〉(0)=1/var(y)×10-2; ⑦ 迭代次數:l=0; 循環: ① 下標賦初值i=1; ③ 判斷σi周圍的點滿足何種連續模式,分別根據式(14)、式(17)、式(20)、式(23)、式(25)估計〈αi〉(l+1); ④ 判斷σi周圍的點滿足何種稀疏模式,根據式(28)估計〈ωi〉(l+1); ⑤ 如果i ⑥ 根據式(30)估計〈αn〉(l+1); ⑦ 如果‖〈σ〉(l+1)-〈σ〉(l)‖ / ‖〈σ〉(l)‖≤10-6或l+1≥lmax程序終止,輸出結果;反之,令l=l+1,程序跳轉至循環第①步。 下面通過仿真驗證所提成像方法的有效性。 實驗1: 分布式無源雷達成像。系統仿真參數與文獻[15]保持一致。另外,設置回波通道的頻率采樣點數為10,接收回波SNR=10 dB。圖4給出了3個目標示例的原始成像模型。針對此類型的擴展目標,圖5 (a)~圖5 (d)是分別采用MF、SBL、文獻[13]和ET-BCS方法的成像結果。可以看出MF方法的成像結果最差,這是由于空間譜的填充是稀疏且非均勻造成的。另外,傳統CS稀疏重構方法(SBL)的成像效果也較差,并且存在較多“虛像”,這是由于目標稀疏性較弱所導致。文獻[13]和ET-BCS方法由于利用了擴展目標的結構信息,因而均能獲得較好的成像結果,如圖5 (c)、圖5 (d)所示。然而,通過對比箭頭所指區域,能夠看出本文方法在重構擴展目標空間位置信息時具有更高的準確性,這是因為ET-BCS是文獻[13]方法的推廣,具有更強的適用性。 圖4擴展目標成像模型 (a)MF (b)SBL (c)文獻[13]方法 (d)ET-BCS圖5ET-BCS與其他方法的無源成像結果對比 實驗2: ISAR成像。仿真使用的目標模型如圖6 (a)所示,是由3DMAX軟件建模得到。其中艦船長度為28 m,寬度約為3.2 m,成像目標與雷達系統的幾何空間構型如圖6 (b)所示,機載雷達沿X負半軸方向勻速運動,速度為300 m/s,雷達成像時間為2.3 s,t=0時,雷達的初始坐標為(5 268.5 m, 1 284.5 m, 4 266.5 m)。另外,雷達發射信號的載頻為5 GHz,帶寬為1 GHz,脈沖持續時間為100 μs,脈沖總數為256,脈內采樣點數為128,其他參數見文獻[16]。接著將雷達系統參數、成像空間構型和目標參數模型代入GRECO圖形電磁仿真軟件,即能得到相應的模擬回波數據。本文在進行ISAR成像之前事先進行了平動補償處理,這里選取前32個脈沖和前32個脈內采樣點作為基礎數據,并額外加入高斯噪聲使得最終的接收回波滿足SNR=5 dB。 (a)3DMAX艦船建模 (b)成像構型圖63DMAX艦船模型及與成像系統空間構型 圖7(a)~(h)依次是RD,FOCUSS,SBL,YALL1,SL0,TVAL3,文獻[13]和ET-BCS方法的成像結果,其中圖中的線框表示艦船的基本輪廓。可以看出RD方法的分辨率最低,這是由于回波數據的欠采樣特性引起;另外,FOCUSS,SBL,YALL1,SL0等傳統CS方法的成像結果中存在較多虛像,這是由于艦船目標的稀疏性較差所導致。TVAL3方法雖然基于TV正則化技術,可以較好地保護圖像的邊緣特性,但該方法沒有進一步利用目標稀疏先驗信息,因此成像結果也不理想。圖7(g)、圖7(h)展示了文獻[13]和ET-BCS方法的成像結果對比。由于這兩種方法均額外利用了擴展目標的結構信息,故成像質量相比其他方法要好很多,并且幾乎不存在任何虛像。但是相比而言,ET-BCS在艦船目標的輪廓、邊緣等信息提取上具有更多的優勢,可以提取到一些額外的強散射點,見圖7(g)~(h)中箭頭的指示區域。這是因為ET-BCS是文獻[13]方法的推廣,它考慮了更多的目標連續模式,并且利用VB求解方法要比Gibbs抽樣方法取得更高的參數提取精度。 (a)RD (b)FOCUSS (c)SBL (d)YALL1 (e)SL0 (f)TVAL3 (g)文獻[13]方法 (h)ET-BCS圖7ET-BCS與其他方法的ISAR成像結果對比 大型剛體目標的距離維及方位維通常存在擴展特性,造成成像場景的散射點較多且呈區域性分布,此時目標空間域的稀疏性相對較差,因此會導致傳統稀疏重構方法的成像性能受限。據此,本文在傳統目標稀疏先驗基礎上,進一步考慮利用擴展目標圖像的結構信息,在貝葉斯框架下基于目標圖像的連續性分布特征,提出了基于擴展目標先驗分布的貝葉斯壓縮感知成像技術。仿真驗證了所提方法的有效性,并展示在相同系統配置模式下相比傳統稀疏重構方法的優勢。 [1]LIU Hongchao, JIU Bo, LIU Hongwei, et al. Superresolution ISAR Imaging Based on Sparse Bayesian Learning[J]. IEEE Trans on Geoscience and Remote Sensing, 2014, 52(8):5005-5013. [2]YANG Lei, ZHOU Jianxiong, HU Lei, et al. A Perturbation-Based Approach for Compressed Sensing Radar Imaging[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16(1):87-90. [3]XU Gang, XING Mengdao, XIA Xianggen, et al. High-Resolution Inverse Synthetic Aperture Radar Imaging and Scaling with Sparse Aperture[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(8):4010-4027. [4]華煜明,趙華,郭軍海. 高速自旋目標ISAR成像的代數重構方法[J]. 雷達科學與技術, 2016, 14(2):134-139. HUA Yuming, ZHAO Hua, GUO Junhai. Algebraic Iterative Imaging Method for Rapidly Rotating Target in ISAR[J]. Radar Science and Technology, 2016, 14(2):134-139.(in Chinese) [5]QIU Wei, ZHAO Hongzhong, ZHOU Jianxiong, et al. High-Resolution Fully Polarimetric ISAR Imaging Based on Compressive Sensing[J]. IEEE Trans on Geoscience and Remote Sensing, 2014, 52(10):6119-6131. [6]WU Q, ZHANG Y D, AHMAD F. Compressive-Sensing-Based High Resolution Polarimetric Through-the-Wall Radar Imaging Exploiting Target Characteristics[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 14(1):1043-1047. [7]DE FREITAS A, DE VILLIERS J P, NEL W A J, et al. Joint Inference of Dominant Scatterer Locations and Motion Parameters of an Extended Target in High Range-Resolution Radar[J]. IET Radar, Sonar & Navigation, 2015, 9(5):519-530. [8]WU Q, ZHANG Y D, AMIN M G, et al. Multi-Task Bayesian Compressive Sensing Exploiting Intra-Task Dependency[J]. IEEE Signal Processing Letters, 2015, 22(4):430-434. [9]TZIKAS D G, LIKAS A C, GALATSANOS N P, et al. The Variational Approximation for Bayesian Inference[J]. IEEE Signal Processing Magazine, 2008, 25(6):131-146. [10]BEVACQUA M, CROCCO L, DONATO L D, et al. Exploiting Sparsity and Field Conditioning in Subsurface Microwave Imaging of Nonweak Buried Targets[J]. Radio Science, 2016, 51(4):301-310. [11]HERMAN M A, STROHMER T. High-Resolution Radar via Compressed Sensing[J]. IEEE Trans on Signal Processing, 2009, 57(6):2275-2284. [12]WANGT,LUX,YUX,etal.AFastandAccurateSparseContinuousSignalReconstructionbyHomotopyDCDwithNon-ConvexRegularization[J].Sensors, 2014, 14 (4):5929-5951. [13]WANGLu,ZHAOLifan,BIGuoan,etal.EnhancedISARImagingbyExploitingtheContinuityoftheTargetScene[J].IEEETransonGeoscienceandRemoteSensing, 2014, 52(9):5736-5750. [14]WANGTianyun,LIUChangchang,DINGLi,etal.SparseImagingUsingImprovedOMPTechniqueinFD-MIMORadarforTargetofftheGrid[C]∥2013Asia-PacificConferenceonSyntheticApertureRadar,Tsukuba,Japan:IEEE, 2013:434-437. [15]WANGTiayun,YUXiaofei,CHENWeidong,etal.High-ResolutionImagingofPassiveRadarBasedon SparseBayesianLearning[J].JournalofElectronics&InformationTechnology, 2015, 37(5):1023-1030. [16]尹治平. 分數階Fourier變換在逆合成孔徑雷達成像處理中的應用[D]. 合肥:中國科學技術大學, 2008.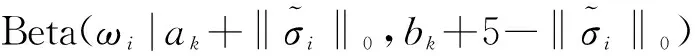
3 仿真實驗與分析

4 結束語

