DMF的力場構建及乙腈-甲醇-DMF三元體系的汽液相平衡模擬

張旗，陳文奇，曾愛武

（化學工程聯合國家重點實驗室，天津大學化工學院，天津 300072）

DMF的力場構建及乙腈-甲醇-DMF三元體系的汽液相平衡模擬

張旗，陳文奇，曾愛武

（化學工程聯合國家重點實驗室，天津大學化工學院，天津 300072）

采用量子化學和Gibbs系綜Monte Carlo模擬相結合的方法，對TraPPE-UA力場中缺失的N,N-二甲基甲酰胺（DMF）力場參數進行了補充，為含DMF多元體系的汽液相平衡模擬奠定了基礎。采用新構建的力場參數，在NVT-Gibbs系綜中計算了DMF的汽液相平衡性質，結果表明該力場能準確計算出DMF的飽和液相密度、蒸氣壓、沸點、臨界值和蒸發焓。在NPT-Gibbs系綜中，采用TraPPE-UA力場分別計算了乙腈-甲醇、DMF-甲醇、DMF-乙腈二元混合物的汽液相平衡性質，并與實驗值進行了比較。模擬結果與實驗值較為吻合，驗證了力場模型的可靠性。最后在NPT-Gibbs系綜中采用TraPPE-UA力場對乙腈-甲醇-DMF三元體系的汽液相平衡數據進行了預測，為設計和優化乙腈和甲醇的萃取分離過程提供了基礎數據。

N,N-二甲基甲酰胺；Monte Carlo模擬；TraPPE-UA力場；乙腈；甲醇；汽液平衡；統計熱力學

引 言

乙腈和甲醇是重要的化工原料。乙腈因具有高溶解性、低沸點、低黏度等特性而被廣泛應用于醫藥、石油工業中[1]。甲醇主要應用于塑料、醫藥等領域，可用來制造乙酸、甲醛、硫酸二甲酯等多種有機產品。在工業廢液中存在大量的乙腈和甲醇混合物，為了避免資源浪費，需對兩者進行分離從而實現對乙腈和甲醇回收利用。乙腈和甲醇在常壓下會形成共沸物，難以用普通的精餾方法進行分離，通常使用萃取精餾方法對兩者進行分離。N,N-二甲基甲酰胺（DMF）是一種性能優異的有機溶劑，被稱為“萬能溶劑”。常在萃取精餾過程中用作萃取劑，已被證實能夠用于萃取分離乙腈和甲醇共沸物[2]。

流體相平衡數據是設計和優化萃取精餾過程的理論基礎。相平衡數據傳統的獲取方法有實驗測量法、活度系數法和狀態方程法。但實驗法的成本較高且受實驗條件所限制。活度系數法和狀態方程法依賴于實驗數據來獲得二元交互作用參數而限制了其預測相平衡數據的能力。近年以來，分子模擬以其計算周期短、計算成本低的優勢在相平衡上的運用非常廣泛，成為一種可以對實驗進行補充的方法[3]。Gibbs系綜Monte Carlo (GEMC)方法[4]因沒有考慮相界面，無須直接計算化學勢而被廣泛應用于純物質和混合物的相平衡計算中[5-6]。

GEMC方法計算結果的準確性主要取決于力場參數的準確性，因此選擇合適的力場對模擬是非常關鍵的。目前常見的力場主要包括TraPPE、OPLS、AMBER、OPPE-AUA、NERD等[7]，其中TraPPE力場是專門針對流體的汽液相平衡性質而開發的，包括聯合原子（UA）力場和全原子（EH）力場兩個版本。TraPPE-UA力場被廣泛應用于烷烴[8]、烯烴[9]、芳香烴[9]、酮[10]、醇[11]、腈類[12]等化合物相平衡性質的計算中。Chen等[11]和Wick等[12]分別采用TraPPE-UA力場計算了甲醇和乙腈的汽液相平衡性質，與實驗值相比，甲醇的液相密度的平均偏差為1.0%，沸點偏差為0.59%，臨界溫度偏差為2.1%；乙腈的沸點偏差為0.28%，臨界溫度偏差為0.73%。然而，目前沒有學者將TraPPE-UA力場拓展到DMF的相平衡計算中。Jorgensen等[13]提出的OPLS-UA力場能夠用于計算DMF在常溫常壓下的液相性質。在此基礎上，為了更深入地研究DMF的液相結構性質及傳遞性質，SM等[14]和CS2等[15]力場相繼被提出。但這些力場是為了研究DMF在常態下的液相性質而提出的，并不適于用來模擬DMF的汽液相平衡性質。

本文首先采用量子化學方法計算了DMF的原子電荷，DMF中氮原子的Lennard-Jones(LJ)參數通過擬合實驗值獲得，其他原子的LJ參數從原始的TraPPE-UA力場中遷移而來，構建了DMF的TraPPE-UA力場。在新構建的力場下對DMF的汽液相平衡性質進行模擬，并與OPLS-UA力場的模擬結果相比較。然后在TraPPE-UA力場下模擬了乙腈-甲醇、DMF-甲醇、DMF-乙腈二元混合物的汽液相平衡數據，并與實驗值進行比較。最后對乙腈-甲醇-DMF三元體系的常壓汽液相平衡數據進行預測，以期為化工分離過程提供基礎數據。

1 力場模型

1.1 DMF的TraPPE-UA力場構建

TraPPE-UA力場是一種聯合原子力場，即將CHx（0 ＜x≤4）視為一個偽原子，其作用中心位于碳原子中心上。力場中采用Lennard-Jones 12-6和庫侖作用勢來描述分子間非鍵相互作用

式中，rij、εij、σij、qi、qj和ε0分別表示原子i和j之間的距離、LJ勢阱深度、LJ半徑、原子電荷和真空介電常數。使用Lorentz-Berthelot混合規則來計算不同原子之間的交叉作用參數

DMF的原子電荷參數采用CHELPG[16]方法進行計算，該方法通過擬合分子表面的靜電勢來獲得原子電荷，是分子力場中計算原子電荷常用的方法。在計算過程中，首先用量化方法HF/6-31+g**對單個DMF分子進行結構優化，獲得最優的分子構型；然后使用CHELPG方法擬合該最優構型下的分子靜電勢來獲得DMF的原子電荷。由于TraPPE力場參數具有可移植性，DMF中除氮原子以外的其他原子的LJ參數（ε，σ）直接從原始的TraPPE-UA力場[10]移植而來。但在原始的TraPPE-UA力場中沒有對DMF中的氮原子進行定義，因此需要對氮原子的LJ參數進行擬合。純物質的力場參數通常可以通過擬合實驗值來獲得[17-18]，本文采用GEMC方法同時擬合DMF在常溫（298.00 K）下的飽和液相密度、沸點（426.15 K）和高溫（580.00 K）下的飽和液相密度、壓力來獲得氮原子的LJ參數。計算出的DMF的原子電荷參數和LJ參數列于表1中，DMF分子中的原子標號如圖1所示。

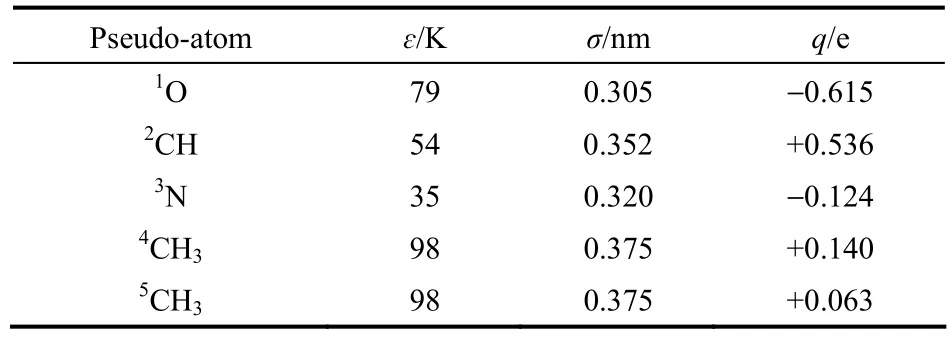
表1 DMF的非鍵相互作用參數Table 1 Non-bonded parameters of DMF

圖1 DMF分子的示意圖Fig.1 Schematic diagram of DMF

由于分子內鍵相互作用對汽液相平衡的模擬結果影響較小，并且為了提高計算效率，力場中采用固定鍵長、鍵角的形式，但是考慮二面角扭轉能。DMF的鍵長、鍵角參數直接來于OPLS-UA力場[13]中，其鍵長、鍵角值列于表2中。采用余弦函數形式來計算二面角扭轉能

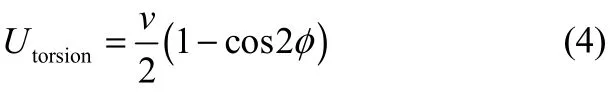
式中，v為二面角扭轉參數，φ為二面角角度。DMF的二面角扭轉參數來于OPLA-UA力場[13]，其具體數值列于表3中。

1.2 乙腈和甲醇的力場模型

由于文獻[11-12]已驗證采用TraPPE-UA力場計算乙腈和甲醇汽液相平衡性質具有較高的準確度和計算效率，因此乙腈和甲醇的力場參數均直接來于原始的TraPPE-UA力場中[11-12]。

表2 DMF的鍵長、鍵角值Table 2 Bond lengths and bond angles of DMF

表3 DMF的二面角參數Table 3 Torsion parameters of DMF

2 模擬細節

采用GEMC方法[4]來計算純組分、二元和三元混合物的汽液相平衡性質，所有的計算均在MCCCS Towhee[19]中進行。

在NVT-Gibbs系綜中對純組分的汽液相平衡性質進行計算，采用周期邊界條件和最小鏡像轉化來計算截斷半徑（rcut=1.4 nm）內的LJ相互作用，在截斷半徑以外采用尾部矯正來計算LJ相互作用，靜電相互作用通過Ewald加和法進行計算。體系中的分子數為300，模擬過程中包括5種移動：體積移動、分子交換、分子再增長、分子平動和轉動。為了使模擬結果更加準確，通過調節體積移動和分子交換的概率，使得每10次MC循環（1次MC循環為N次移動，N指總分子數）中大約有1次MC循環被接受，剩余的概率由其他3種移動均分。模擬分為預平衡段和平衡段，預平衡段至少包括5×104步MC循環，平衡段包括5×104步MC循環，同時將平衡段分成5個模塊進行統計平均。

二元和三元體系的汽液相平衡模擬在NPT-Gibbs系綜中進行，體系中分子數分別為500和600。體積移動、分子交換、分子再增長、分子平動和轉動的概率分別為0.1%、29.9%、24%、23%、23%。二元體系的預平衡段至少包括10×104步MC循環，平衡段包括5×104步MC循環。三元體系的預平衡段至少包括15×104步MC循環，平衡段包括10×104步MC循環。

3 結果與討論

3.1 DMF純組分的汽液相平衡模擬

采用新構建DMF的TraPPE-UA力場，模擬了DMF在360.00～580.00 K之間的汽液相平衡性質。并且為了進行對比，同時采用文獻中的OPLS-UA力場[13]對DMF的汽液相平衡進行了模擬。

由于DMF在高溫下飽和液相密度的實驗值還未在文獻中公開報道，因此使用Rackett方程[20]對DMF的飽和液相密度進行關聯。DMF的汽液相平衡曲線如圖2所示。從圖2可以看出，與關聯值相比，采用TraPPE-UA力場計算的DMF飽和液相密度非常準確，其最大的液相密度相對偏差為0.94%。而采用OPLS-UA力場計算的DMF飽和液相密度雖然在低溫時較為準確，但隨溫度升高偏差逐漸增大，其最大液相密度相對偏差為7.33%。

圖2 DMF的汽液相平衡圖Fig.2 Vapor-liquid equilibria of DMF

DMF飽和蒸氣壓的模擬結果如圖3所示。由于缺乏DMF在高溫下的蒸氣壓力實驗值，因此使用Antoine方程[20]對DMF的飽和蒸氣壓進行關聯。從圖3可以看出，與關聯值相比，采用TraPPE-UA力場計算的DMF飽和蒸氣壓較為準確，但采用OPLS-UA力場計算的DMF飽和蒸氣壓偏低。通過對Clausius-Clapeyron圖中的模擬數據點進行內插獲得DMF的沸點值，其結果列于表4中。與實驗值相比，采用TraPPE-UA力場計算的DMF沸點僅偏低1.05 K，而采用OPLS-UA力場計算的DMF沸點值偏高5.85 K。

圖3 DMF的飽和蒸氣壓-溫度圖（插圖為DMF的Clausius-Clapeyron圖）Fig.3 Pressure-temperature diagram of DMF(insert figure shows Clausius-Clapeyron plot of DMF)

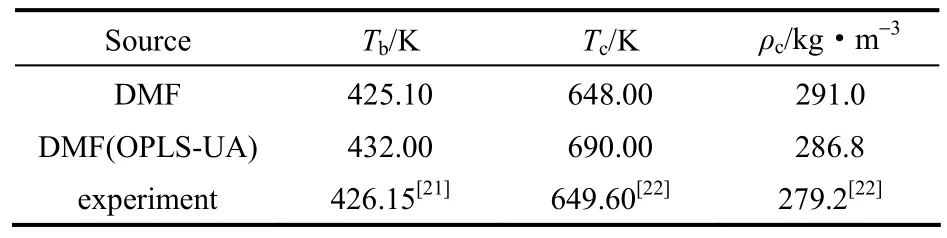
表4 模擬預測的DMF的沸點和臨界參數Table 4 Predicted normal boiling points and critical parameters of DMF

DMF的臨界溫度、密度分別通過式(5)[23]、式(6)[24]擬合DMF在360.00～580.00 K之間的飽和氣液相密度值獲得

式中，ρl、ρv、Tc、ρc、T分別為飽和液相密度、飽和氣相密度、臨界溫度、臨界密度和模擬溫度，臨界指數β=0.325，A、B為常數。DMF的臨界溫度和臨界密度計算結果如圖2、表4所示。從圖2、表4可以看出，兩個力場預測出的臨界密度值差異較小，但預測出的臨界溫度值差異較大。與實驗值相比，采用TraPPE-UA力場計算出的臨界溫度的相對偏差僅為0.25%，但采用OPLS-UA力場計算出的臨界溫度的相對偏差達到了6.2%。

DMF的蒸發焓在模擬過程中根據式(7)進行計算而獲得

式中，下角標v和l分別表示氣相和液相，U表示每摩爾的分子間勢能，V表示摩爾體積，P表示氣相壓力。DMF蒸發焓的模擬結果如圖4所示，并使用對應狀態法[20]對DMF的蒸發焓進行關聯。從圖4可以看出，與關聯值相比，采用OPLS-UA力場計算的DMF蒸發焓在整個溫度范圍內都明顯偏高，采用TraPPE-UA力場計算的DMF蒸發焓在低溫時偏高，但在高溫時比較準確。

圖4 DMF的蒸發焓圖Fig.4 Heats of vaporization of DMF

通過以上對比分析可知，與OPLS-UA力場相比，采用新構建的TraPPE-UA力場進行模擬得到的DMF的飽和液相密度、飽和蒸氣壓、沸點、蒸發焓及臨界性質都有明顯的改善。

3.2 二元混合物的汽液相平衡模擬

3.2.1 乙腈-甲醇 文獻[11-12]已驗證了TraPPE-UA力場能夠準確預測乙腈和甲醇純組分的汽液相平衡性質，但尚未驗證TraPPE-UA力場能否準確描述乙腈和甲醇二元混合物的汽液相平衡性質。 因此，本文采用原始的TraPPE-UA力場建立乙腈和甲醇的模型，在101.3 kPa下336.96～350.19 K范圍內選取6個溫度點進行乙腈和甲醇二元共沸物的汽液相平衡模擬，并與實驗值[25]進行比較。實驗值是在101.3 kPa下，通過平衡釜測量所得，測得乙腈和甲醇的共沸溫度為337.00 K，共沸點組成為16%的乙腈和84%的甲醇。二元共沸物的模擬結果列于表5中。從表5可以看出，乙腈在氣相中的組成與實驗值基本吻合，但在液相中的組成與實驗值相比稍有偏差。其氣相組成的平均絕對偏差為0.008，液相組成的平均絕對偏差為0.030。總體來說，模擬結果與實驗值較為一致，說明TraPPE-UA力場能夠較為準確地預測乙腈和甲醇二元混合物的汽液相平衡性質。

表5 在101.3 kPa下采用TraPPE-UA力場計算的乙腈和甲醇二元混合物汽液相平衡數據Table 5 Vapor-liquid equilibria data of acetonitrile-methanol at 101.3 kPa calculated by TraPPE-UA force field

3.2.2 DMF-甲醇和DMF-乙腈 基于新構建的DMF的TraPPE-UA力場，在101.3 kPa下進行DMF-甲醇和DMF-乙腈二元混合物的汽液相平衡模擬，并將模擬結果與實驗值[26-27]進行比較，驗證能否將新構建的力場參數拓展到二元混合物的汽液相平衡計算中。

圖5為DMF和甲醇二元混合物在101.3 kPa下的溫度-組成曲線。從圖5可以看出，DMF和甲醇的模擬值與實驗值基本吻合。與實驗值相比，DMF的液相組成的平均絕對偏差為0.023，氣相組成的平均絕對偏差為0.012。

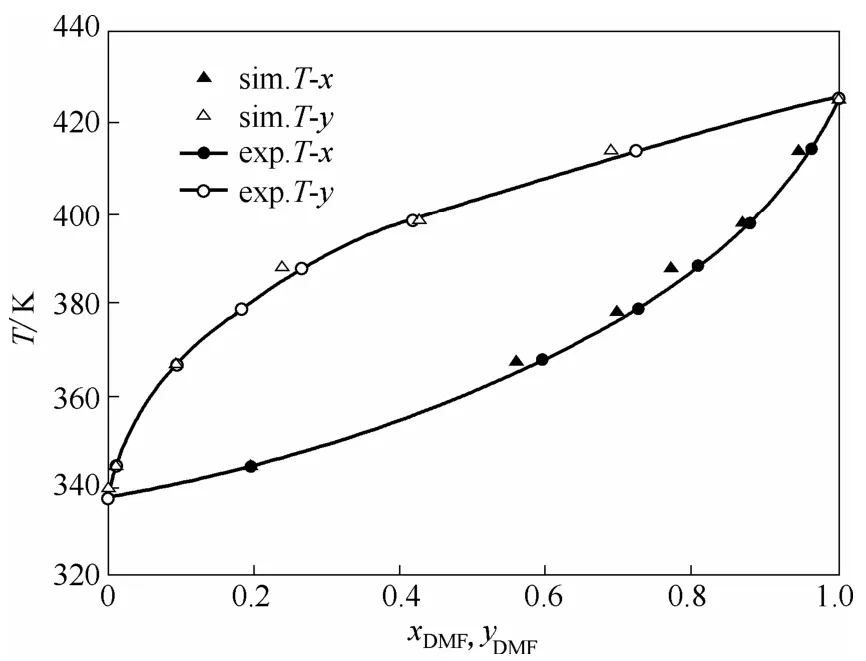
圖5 DMF-甲醇在101.3 kPa下的汽液相平衡圖Fig.5 Vapor-liquid equilibria of DMF-methanol at 101.3 kPa

圖6為DMF和乙腈的二元混合物在101.3 kPa下的溫度-組成曲線，從圖6可以看出，DMF和乙腈的模擬值與實驗值較為吻合。與實驗值相比，DMF的液相組成的平均絕對偏差為0.031，氣相組成的平均絕對偏差為0.021。

圖6 DMF-乙腈在101.3 kPa下的汽液相平衡圖Fig.6 Vapor-liquid equilibria of DMF-acetonitrile at 101.3 kPa

從DMF-甲醇和DMF-乙腈的模擬結果可以發現，采用TraPPE-UA力場預測純物質汽液相平衡時具有較高的模擬精度，但預測二元混合物汽液相平衡時模擬結果會稍有偏差。原因是相對于純組分，二元體系中分子之間更為復雜的交互作用會增大力場的預測難度，從而影響模擬的準確度。但總體的模擬偏差不大，表明新構建的DMF的TraPPE-UA力場能夠較為準確地描述DMF-甲醇和DMF-乙腈二元混合物的汽液相平衡性質，進一步驗證了新構建的力場的準確性，拓展了該力場的適用范圍。

3.3 乙腈-甲醇-DMF三元體系的汽液相平衡模擬

乙腈、甲醇和DMF三元混合物在101.3 kPa下的汽液相平衡數據尚未見文獻進行報道。因此，本文基于新構建的DMF的TraPPE-UA力場，采用GEMC方法預測了乙腈-甲醇-DMF三元混合物在101.3 kPa時，360.00、370.00 K溫度下的汽液相平衡數據，并將預測結果與UNIQUAC方程[28]估算的結果進行比較。預測結果如表6和圖7所示。UNIQUAC方程中的二元交互作用參數通過關聯乙腈-甲醇、DMF-甲醇、DMF-乙腈3個二元體系在101.3 kPa下的汽液相平衡實驗數據[25-27]所獲得，其具體數值列于表7中。

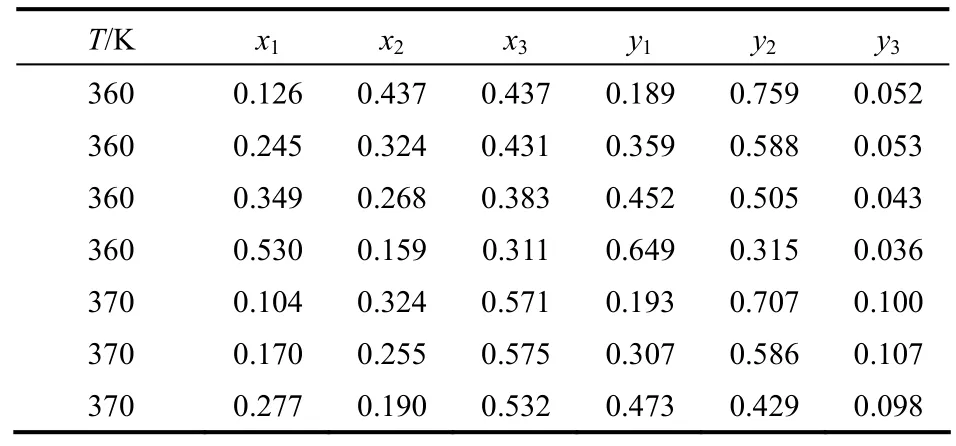
表6 在101.3 kPa下采用TraPPE-UA力場計算的乙腈(1)-甲醇(2)-DMF(3)三元混合物汽液相平衡數據Table 6 Vapor-liquid equilibria data of acetonitrile(1)-methanol(2)-DMF(3) at 101.3 kPa calculated by TraPPE-UA force field

從圖7可以看出，與UNIQUAC方程估算的結果相比，DMF在液相和氣相中的含量稍微偏高。總體來看，模擬結果與UNIQUAC方程估算的結果具有一致的趨勢，但GEMC模擬不需要根據實驗值來擬合二元交互作用參數即可對三元體系的汽液相平衡數據直接進行預測。

表7 UNIQUAC方程的二元交互作用參數Table 7 Binary interaction parameters of UNIQUAC model

4 結 論

本文基于TraPPE-UA力場模型，構建了一套針對DMF汽液相平衡模擬的力場參數。該力場能夠準確地計算出DMF的汽液相平衡數據，并且通過與OPLS-UA力場計算的結果進行對比可知：新構建的TraPPE-UA力場能更好地描述DMF的汽液相平衡性質。

使用原始的TraPPE-UA力場建立乙腈和甲醇的模型，進行了乙腈-甲醇二元混合物的汽液相平衡模擬，模擬值與實驗值較為吻合。基于新構建的DMF的TraPPE-UA力場，計算了DMF-甲醇、DMF-乙腈的汽液相平衡數據，模擬結果與實驗值較為一致，進一步驗證了新構建的力場的準確性，拓展了該力場的適用范圍。

采用GEMC模擬對乙腈-甲醇-DMF三元混合物的常壓汽液相平衡數據進行了預測，預測結果與UNIQUAC方程估算的結果較為一致，為設計和優化DMF萃取分離乙腈和甲醇的精餾過程提供了基礎數據。

圖7 乙腈-甲醇-DMF在101.325 kPa，360.00、370.00 K下的汽液相平衡圖Fig.7 Vapor-liquid equilibria of acetonitrile-methanol-DMF at 101.325 kPa，360.00 K，370.00 K

符 號 說 明

A,B——常數

ΔH——蒸發焓，kJ·mol-1

P——氣相壓力，kPa

qi,qj——原子電荷，e

rij——原子間的距離，nm

Tc,T——分別為臨界溫度，模擬溫度，K

U(rij)——非鍵作用扭轉勢能，K

Ul,Uv——每摩爾的分子間勢能，kJ·mol-1

Utorsion——二面角勢能，K

Δuij,Δuji——UNIQUAC方程交互作用參數，J·mol-1

V——摩爾體積，m3·mol-1

v——二面角扭轉參數，K

β——臨界指數

εij——LJ勢阱深度，K

ε0——真空介電常數，F·m-1

ρl,ρv,ρc——分別為飽和液相密度、飽和氣相密度、臨界密度，kg·m-3

σij——LJ半徑，nm

φ——二面角角度，rad

下角標

c——臨界點

i,j——原子i，j

l——液相

torsion——二面角

v ——氣相

[1] 李文秀, 張琦, 張親親, 等. 含離子液體乙腈-正丙醇體系的等壓汽液平衡[J]. 化工學報, 2015, 66(S1): 38-44. LI W X, ZHANG Q, ZHANG Q Q,et al. Isobaric vapor-liquid equilibrium for system of acetonitrile-n-propanol system containing ionic liquids[J]. CIESC Journal, 2015, 66(S1): 38-44.

[2] 于洋, 白鵬, 莊瓊紅. 萃取精餾分離甲醇-乙腈的研究[J]. 化學工程, 2011, 39(6): 36-39. YU Y, BAI P, ZHUANG Q H. Separation of methanol-acetonitrile by extractive distillation[J]. Chemical Engineering (China), 2011, 39(6): 36-39.

[3] KAMATH G, ROBINSON J, POTOFF J J. Application of TraPPE-UA force field for determination of vapor-liquid equilibria of carboxylate esters[J]. Fluid Phase Equilibria, 2006, 240(1): 46-55.

[4] PANAGIOTOPOULOS A Z. Direct determination of fluid phase equilibria by simulation in the Gibbs ensemble: a review[J]. Molecular Simulation, 1992, 9(1): 1-23.

[5] 楊華明, 張敏華, 馬靜. 丁烯醛及丁烯醛-乙醛二元體系汽液相平衡模擬[J]. 化工學報, 2015, 66(5): 1627-1632. YANG H M, ZHANG M H, MANG J. Vapor-liquid equilibrium simulation for crotonaldehyde and its mixture with ethanol[J]. CIESC Journal, 2015, 66(5): 1627-1632.

[6] DONG X, GUAN X, JIANG Y,et al. Extension of the TraPPE-UA force field to the simulation of vapor-liquid phase equilibria of vinyl acetate system[J]. Journal of Molecular Liquids, 2015, 209: 520-525.

[7] GUEVARA-CARRION G, HASSE H, VRABEC J. Thermodynamic properties for applications in chemical industryviaclassical force fields[J]. Topics in Current Chemistry, 2012, 307: 201-249.

[8] MARTIN M G, SIEPMANN J I. Transferable potentials for phase equilibria(Ⅰ): United-atom description ofn-alkanes[J]. The Journal of Physical Chemistry B, 1998, 102(14): 2569-2577.

[9] WICK C D, MARTIN M G, SIEPMANN J I. Transferable potentials for phase equilibria(Ⅳ): United-atom description of linear and branched alkenes and alkylbenzenes[J]. The Journal of Physical Chemistry B, 2000, 104(33): 8008-8016.

[10] STUBBS J M, POTOFF J J, SIEPMANN J I. Transferable potentials for phase equilibria(Ⅵ): United-atom description for ethers, glycols, ketones, and aldehydes[J]. The Journal of Physical Chemistry B, 2004, 108(45): 17596-17605.

[11] CHEN B, POTOFF J J, SIEPMANN J I. Monte Carlo calculations for alcohols and their mixtures with alkanes. Transferable potentials for phase equilibria(Ⅴ): United-atom description of primary, secondary, and tertiary alcohols[J]. The Journal of Physical Chemistry B, 2001, 105(15): 3093-3104.

[12] WICK C D, STUBBS J M, RAI N,et al. Transferable potentials for phase equilibria(Ⅶ): Primary, secondary, and tertiary amines, nitroalkanes and nitrobenzene, nitriles, amides, pyridine, and pyrimidine[J]. The Journal of Physical Chemistry B, 2005, 109(40): 18974-18982.

[13] JORGENSEN W L, SWENSON C J. Optimized intermolecular potential functions for amides and peptides. Structure and properties of liquid amides[J]. Journal of the American Chemical Society, 1985, 107(3): 569-578.

[14] SCHOESTER P C, ZEIDLER M D, RADNAI T,et al. Comparison of the structure of liquid amides as determined by diffraction experiments and molecular dynamics simulations[J]. Zeitschrift für Naturforschung A, 1995, 50(1): 38-50.

[15] CHALARIS M, SAMIOS J. Systematic molecular dynamics studies of liquidN,N-dimethylformamide using optimized rigid force fields: investigation of the thermodynamic, structural, transport and dynamic properties[J]. The Journal of Chemical Physics, 2000, 112(19): 8581-8594.

[16] LéVY B, ENESCU M. Theoretical study of methylene blue: a new method to determine partial atomic charges; investigation of the interaction with guanine[J]. Journal of Molecular Structure: THEOCHEM, 1998, 432(3): 235-245.

[17] SOKKALINGAM N, KAMATH G, COSCIONE M,et al. Extension of the transferable potentials for phase equilibria force field to dimethylmethyl phosphonate, sarin, and soman[J]. The Journal of Physical Chemistry B, 2009, 113(30): 10292-10297.

[18] KETKO M B H, KAMATH G, POTOFF J J. Development of an optimized intermolecular potential for sulfur dioxide[J]. The Journal of Physical Chemistry B, 2011, 115(17): 4949-4954.

[19] MARTIN M G. MCCCS Towhee: a tool for Monte Carlo molecular simulation[J]. Molecular Simulation, 2013, 39(14/15): 1212-1222.

[20] PERRY R H, GREEN D W. Perry's Chemical Engineers' Handbook[M]. 8th ed. New York: McGraw-Hill, 2008: 477-497.

[21] HORIKOSHI S, IIDA S, KAJITANI M,et al. Chemical reactions with a novel 5.8-GHz microwave apparatus(Ⅰ): Characterization of properties of common solvents and application in a Diels-Alderorganic synthesis[J]. Organic Process Research & Development, 2008, 12(2): 257-263.

[22] TEJA A S, ANSELME M J. The critical properties of thermally stable and unstable fluids(Ⅰ): 1985 results[J]. AIChE Symp. Ser., 1990, 86(279): 115-121.

[23] ROWILDSON J S, WIDOM B. Molecular Theory of Capillarity [M]. New York: Oxford University Press, 1989: 261.

[24] ROWILDSON J S, WIDOM B. Liquids and Liquid Mixtures [M]. 3rd ed. London: Butterworth, 1982: 70-75.

[25] LI Y, BAI P, ZHUANG Q. Isobaric vapor-liquid equilibrium for binary system of methanol and acetonitrile[J]. Fluid Phase Equilibria, 2013, 340: 42-45.

[26] BITTRICH H J, FLEISCHER W. Untersuchungen des gleichgewichtes flüssigkeit-dampf im system methanoldimethylformamid[J]. Journal für Praktische Chemie, 1963, 20(3/4): 151-160.

[27] 曾紅, 姚舜, 劉其松, 等. 乙腈-正丙醇-N,N-二甲基甲酰胺體系的等壓汽液平衡[J]. 高校化學工程學報, 2011, 25(3): 365-369. ZENG H, YAO S, LIU Q S,et al. Isobaric vapor-liquid equilibria of acetonitrile-propan-1-ol-N,N-Dimethyl formamide systems[J]. Journal of Chemical Engineering of Chinese Universities, 2011, 25(3): 365-369.

[28] ANDERSON T F, PRAUSNITZ J M. Application of the UNIQUAC equation to calculation of multicomponent phase equilibria(Ⅰ): Vapor-liquid equilibria[J]. Industrial & Engineering Chemistry Process Design and Development, 1978, 17(4): 552-561.

Force field construction for DMF and vapor-liquid phase equilibrium simulation of acetonitrile-methanol-DMF

ZHANG Qi, CHEN Wenqi, ZENG Aiwu
(State Key Laboratory of Chemical Engineering,School of Chemical Engineering and Technology,Tianjin University,Tianjin300072,China)

An extensional TraPPE-UA force field forN,N-dimethyl-formamide(DMF) was developed by combination of the quantum chemistry calculation and Gibbs ensemble Monte Carlo simulation, which lays the foundation for the simulation of vapor-liquid phase equilibrium with DMF. First of all, the vapor-liquid phase equilibrium for DMF was calculated in the NVT-Gibbs ensemble by using this new force filed. The results show that the new force field can be used to accurately calculate the saturated liquid densities, vapor pressures, normal boiling point, critical point and heats of vaporization of DMF. Secondly, the vapor-liquid equilibrium for binary mixtures of acetonitrile-methanol, DMF-methanol, DMF-acetonitrile were computed in the NPT-Gibbs ensemble by adopting the TraPPE-UA force field. These simulation results were in good agreement with the experimental data, which validated the reliability of this model. Finally, the vapor-liquid equilibrium data of ternary mixture of acetonitrile-methanol-DMF were predicted in the NPT-Gibbs ensemble, which can provide basic data for design and optimization of the separation process of acetonitrile and methanol.

N,N-dimethylformamide; Monte Carlo simulation; TraPPE-UA force field; acetonitrile; methanol; vapor-liquid equilibrium; statistical thermodynamics

ZENG Aiwu, awzeng@tju.edu.cn

O 642.4+2

：A

：0438—1157（2017）02—0567—08

10.11949/j.issn.0438-1157.20161256

2016-09-08收到初稿，2016-10-15收到修改稿。

聯系人：曾愛武。

：張旗（1993—），女，碩士研究生。

國家科技支撐計劃項目（2007BAB24B05）。

Received date: 2016-09-08.

Foundation item: supported by the National Key Technology Research and Development Program of the Ministry of Science and Technology of China (2007BAB24B05).