關于初中數學圖形等面積拼接問題的教學之探索

文志遠

摘要：初中數學中許多幾何數學問題看似與面積不相關，但是卻可以靈活地利用面積法予以解決。面積作為幾何的一種重要結構，學生要學會將其作為解題的重要工具與手段，探索幾何數學問題求解的正確解答方法。而在圖形等面積拼接教學中，“剪圖與拼接”教學是引導學生解決這一類數學問題的重要教學方法，筆者將通過初中數學圖形等面積拼接問題進行“剪圖與拼接”教學的分析與探討，以供參考。

關鍵詞：初中數學；幾何問題；面積法；拼接

在面積法中，剪圖與拼接是其最為直接且易于理解的解題思路，具有思路靈活與答案不唯一的特點。同時，這一解題思路對學生提出的要求就是要針對幾何問題進行多方面、多層次以及多角度的思考與探索，在深入理解與領悟剪圖與拼接的要點之后，將原圖形的面積以全新、直觀、易求解的圖形面積展現出來[1]。

1 初中數學圖形等面積拼接現狀

在初中數學勾股定理的課堂教學后，呈現給學生的新知識點之一就是圖形等面積拼接問題，旨在培養學生對這類數學問題的解決能力。教師在教學過程中，關鍵是要引導學生去將等面積圖形拼接思路與拼接方法進行歸納總結，形成其對正方形拼接問題的正確深刻認識，著重針對剪圖與拼圖方法的教學難點進行授課。但是在引導學生去聯想、模仿趙爽弦圖進行正方形拼接的時候，卻存在這樣的困境：在分割線減少的情況下，學生難以擺脫趙爽弦圖的禁錮，難以找到分割線不過格點的好方法，也就難以解決這類數學題。因此，要真正培養學生解決這類數學問題的能力，就需要引導其理解與領悟“剪邊長、拼直角”的剪圖與拼圖原理。

2 初中數學幾何圖形等面積拼接問題教學方法

2.1 “5個等面積且呈一字型的小正方形——1個同等面積大正方形”剪拼教學

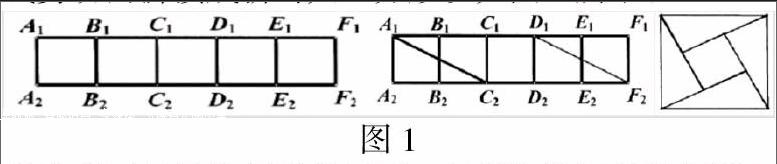
在教學過程中，教師發揮著重要的引導作用，讓學生可以在教師的有效引導下與自身學習相結合，發現數學中的問題，并予以解決，也利于避免學習誤區，防止定式思維對學習的影響。比如在5個等面積且呈一字型的小正方形中，教師可以引導學生從拼圖前后面積不變的角度去深入思考，每個小正方形邊長為1，5個一字型排開的小正方形總面積為1×5=5，因此，所需要拼接的同等面積大正方形的邊長則為 ，所以要在一字型5個小正方形組成的矩形中找到邊長為 的分割線。而根據前面課程的勾股定理，我們可以得知長為2、寬為1的長方形對角線即為另一邊長 ，可以將其作為分割線，再讓學生沿著分割線剪切而拼接成新的大正方形。如圖1所示：

教師在引導學生剪圖拼接后，也要讓學生對其分割方法進行檢驗、歸納與總結，可以得到切邊長、拼直角的解題方法。

2.2 “改變位置后的5個小正方形——1個同等面積大正方形”剪拼教學

與2.1不同的是，5個小正方形只是位置發生變化，其他方面條件一樣。

2.2.1 學生在趙爽弦圖思維定式下的圖形分割法

在往常的教學過程中，常見學生擺脫不了趙爽弦圖的思維定式，將圖形剪出1個正方形與4個直角三角形，如圖2所示：

2.2.2 擺脫趙爽弦圖思維定式下的圖形分割法

要擺脫趙爽弦圖進行幾何數學圖形等面積的剪拼，可以用分割線分成三個部分，將其中2塊移動拼接成新的等面積大正方形，如圖3所示：

2.2.3 圖形分割法的延伸歸納

教師要引導學生在解決問題后，引出問題，進行解題方法的延伸歸納[2]。比如，教師可以引出“是否在保證拼得正方形邊長確定的分割線之間相互垂直的情況下，能夠剪拼形成更大的同等面積正方形”這一問題。教師可以讓學生進行正方形紙片剪拼試驗方法，讓學生親身操作，作出邊長為 的分割線，在其相互垂直的情況下，可以作出2組圖形剪拼如圖4所示：

由此可見，學生已經不再局限于趙爽弦圖而進行圖形拼接。然而，教師還要注意，不能讓學生步出了一個思維定式而又走進了另一個思維定式。學生在利用正方形紙進行 為邊長的分割線時，一般是通過勾股定理得出以1和2為直角邊長的三角形斜邊長，但是其分割線頂點出現了局限性問題，即都處于格點處。那么，教師要引導學生進行更深層次與更多方面的思考：以 為邊長，同時又相互垂直的分割線還能有其它分割法嗎？學生在教師的引導下，可以發現，分割線的平移作用并不會對相互垂直的分割線位置與數量造成任何影響。也就是說，分割線的意義就是將所要拼接的大正方形邊長剪切出來，所以最后拼圖時要使得分割線朝外拼接，而分割線互相垂直的意義，就是通過垂直分出四個直角，將其作為新正方形的內角，最終形成完整的新大正方形，如圖5所示：

2.3 “2個任意大小正方形——1個同等面積大正方形”剪拼教學

可以將2個大小正方形設為邊長分別是1和2，要將其進行剪圖拼接形成新的1個同等面積大正方形。原圖形面積為兩個小正方形面積之和，即是1?+2?=5。因此，所需要拼接的新正方形面積也是5，其邊長則為 ，可將采用如圖6所示的剪圖與拼接方法：

其中，AB=CD=1，BC=DE=2，由左圖作出分割線AC和CE，邊長即為 ，是所需要拼接的新正方形邊長，沿著分割線進行剪切，將2個大小正方形分成3部分，并將剪切出來的1和2部分紙片拼接在1?和2?位置，最終形成新的等同面積大正方形ACEF，且邊長為 。

3 初中數學圖形等面積拼接問題的思考及有效策略

初中數學圖形等面積拼接問題的教學環節創設，旨在讓學生可以不斷去探索剪切與拼接正方形的各種新方法，但是目前卻普遍存在學生難以擺脫趙爽弦圖的拼接思路，數學思維呈現定式特征。數學是一門抽象且深奧的課程，需要學生不斷去思考，去探索，去突破。因此，要做到以下幾點，強化初中數學圖形等面積拼接教學[3]：

首先，要強化教師的引導作用。教師要正確認識自身在課堂上的主導地位，在尊重學生主體地位的前提下，充分發揮自身的引導作用，及時帶領學生走出誤區，進而走進新天地，并且要進行新知識的拓展與延伸，鼓勵與引導學生去更深層次與另辟角度去探索新問題與新方法，在多方面觀察的前提下進行深入學習與思考。

其次，要強化學生的幾何畫圖能力。在初中數學圖形等面積拼接教學中，作出圖形分割線是十分重要的學習內容，學生要在這個過程中切身體會怎樣去拼接全新的等面積正方形，借助剪刀與紙片開展實際操作，加深自身的記憶，強化自己對這一知識的訓練。此外，還可運用其它技巧，比如用數字來對所需拼接的圖形進行順序標注，從而讓自己更清晰直觀地看到拼接前后圖片的位置變化，利于提高操作效率與實踐能力。

4 結束語

總的來說，初中數學圖形等面積拼接問題教學工作，需要在教師的有效引導下讓學生去學，教師也要在學生學習過程中去加深教學，推動學生不斷去發現新問題，進而分析問題，在歸納與總結的過程中培養與提高其解決問題能力，并且養成其創新探索的學習好習慣，使其整個學習生涯都受益。

參考文獻：

[1]李忠琴.面積法在圖形剪、拼中的運用[J].基礎教育論壇，2010，（11）：27.

[2]許雯.對初中數學圖形等面積拼接問題的教學反思[J].北京教育學院學報（自然科學版），2012，04：54-56.

[3]陳琦琨.初中數學教學中面積法的應用探討[J].中學課程輔導（教師通訊），2015，06：53.