矩陣形式下的韋達(dá)定理

葉雉鳩

(陜西財(cái)經(jīng)職業(yè)技術(shù)學(xué)院，陜西 咸陽(yáng) 712000)

矩陣形式下的韋達(dá)定理

葉雉鳩

(陜西財(cái)經(jīng)職業(yè)技術(shù)學(xué)院，陜西 咸陽(yáng) 712000)

把一元高次代數(shù)式表示成矩陣形式，由方陣的特征多項(xiàng)式的定義可以得知一元高次方程的解是矩陣的特征值。如果能夠把矩陣對(duì)角化，那么一元高次方程的解也就得到了。對(duì)于一元5次方程根與系數(shù)的關(guān)系(韋達(dá)定理)建立矩陣形式下的表示關(guān)系，求出了五階范德蒙德矩陣的逆矩陣。顯然，范德蒙德矩陣的逆矩陣可以有一般的表示通式。

韋達(dá)定理；一元高次方程；范德蒙德矩陣；矩陣形式

1 一元高次方程的解就是矩陣的特征值

首先，一元高次代數(shù)式可以表示成矩陣式(1)

(1)

其次，由方陣的特征多項(xiàng)式的定義

得知，一元高次方程的解是下列矩陣式(2)的特征值(根)

(2)

如果能夠把矩陣A(2)對(duì)角化，那么一元高次方程的解也就得到了。若n階矩陣A與對(duì)角矩陣

(3)

相似，則λ1,λ2,…,λn即是A的n個(gè)特征值[1]。再根據(jù)相似矩陣的定義得知，應(yīng)有可逆矩陣P，使P-1AP=Λ

即AP=PΛ

2 范德蒙德矩陣及其逆矩陣

以一元五次方程為例，探索AP=PΛ中的矩陣P的形式

x5+a1x4+a2x3+a3x2+a4x+a5=0

由式(2)、(3)得式(4)、(5)

(4)

其中-a5、-a4、-a3、-a2、-a1均可用韋達(dá)定理的代數(shù)形式表示。

(5)

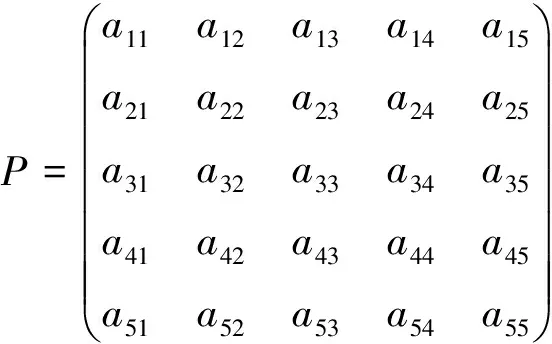
由AP=PΛ得式(6)

(6)

由式(6)推出式(7)

(7)

將式(7)代入AP=PΛ中之后，對(duì)角矩陣可以消掉。

ACD=CDΛ,AC=CDΛD-1=CΛ

即有式(8)

(8)

C為范德蒙德矩陣，而且C是P的簡(jiǎn)潔形式。這時(shí)，不妨令P=C。

(9)

對(duì)于五階范德蒙德矩陣P式(9)，如何求其逆矩陣？ 根據(jù)定理：若|P|≠0，則矩陣P可逆，且

其中P*為矩陣P的伴隨矩陣[1]。 由范德蒙德行列式的值[1]和行列式的性質(zhì)3就可以求出五階范德蒙德矩陣的逆矩陣。 經(jīng)過(guò)計(jì)算推導(dǎo)，五階范德蒙德矩陣P式(9)的逆矩陣為式(10)

(10)

其中

因?yàn)镻-1又可以提取出來(lái)一個(gè)對(duì)角矩陣T,

P-1=TS,所以S(11)是P-1的簡(jiǎn)潔形式。

于是，由A=PΛP-1得

(11)

其中

……

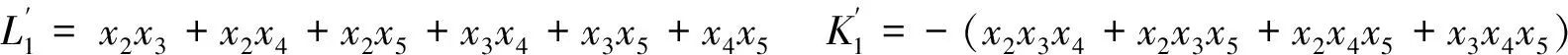
至此，韋達(dá)定理就可應(yīng)用矩陣表述為: A=PΛP-1或者A=S-1ΛS,

其中A,Λ,P,P-1,S分別用式(4)、(5)、(9)、(10)、(11)表示。

3 用一元二次方程進(jìn)行驗(yàn)證

x2+a1x+a2=0

由式(4)、(5)、(9)、(10)、(11)推知式(12)～(16)

(12)

(13)

(14)

(15)

(16)

因?yàn)?/p>

所以公式A=PΛP-1成立。

因?yàn)?/p>

所以公式A=S-1ΛS亦成立。

驗(yàn)畢。

對(duì)于一元n次方程根與系數(shù)的關(guān)系(韋達(dá)定理)亦可以建立以上矩陣形式下的表示關(guān)系。

[1] 同濟(jì)大學(xué)數(shù)學(xué)教研室.《線性代數(shù)》(第三版)[M].北京：高等教育出版社，1999：14,25,55,144.

責(zé)任編輯 王菊平

Matrix form of Viete theorem

YE Zhi-jiu

(Shaanxi Technical College of Finance & Economics, Xianyang 712000, Shaanxi， China)

Firstly, the high degree algebraic with an unknown is expressed as a matrix. According to the definition of the characteristic polynomial of a square matrix, we know that the solution of a higher order equation is the characteristic value of the matrix. If we can get the diagonalization matrix of the matrix, the solution of the equation of higher order is obtained. When establishing matrix representation for the relationship between the root and coefficient of the five-order equation with an unknown (the Viete theorem), the inverse matrix of the five-order Vandermonde matrix is obtained. Obviously, the inverse matrix of Vandermonde matrix can have a general representation formula.

Viete theorem; once basic equation of higher degree; Vandermonde matrix; matrix form

O156.1

A

1003-8078(2016)06-0019-04

2016-10-25 doi 10.3969/j.issn.1003-8078.2016.06.06

葉雉鳩，男，陜西乾縣人，副教授，碩士，主要研究方向?yàn)閿?shù)學(xué)和經(jīng)濟(jì)學(xué)。