初中數(shù)學圓輔助線作法的規(guī)律性探究

周兆權(quán)●

江蘇省常州市新北區(qū)實驗中學(213002)

?

初中數(shù)學圓輔助線作法的規(guī)律性探究

周兆權(quán)●

江蘇省常州市新北區(qū)實驗中學(213002)

輔助線的作法在初中數(shù)學教學過程中是十分重要的，特別是在初二年級的平面幾何課程學習中尤為重要.輔助線就是為了證明題目，在原來圖形的基礎上添加的線，它的目的明確，就是為了解決學生在數(shù)學中遇到的一些問題.初中數(shù)學教師在教學的過程中發(fā)現(xiàn)，輔助線是存在一定的規(guī)律的.

初中數(shù)學；輔助線；規(guī)律性研究

一、初中數(shù)學輔助線作法

初中數(shù)學輔助線，顧名思義就是輔助學生解題用的，在數(shù)學中作輔助線一般可分為三個步驟：

(1)確定圖形中的關鍵點，比如中點、交點等等；

(2)在圖形中作一條關鍵輔助線，使此輔助線與圖形中的線存在一定的關系，比如垂直線段等等，從而使輔助線的功能能夠充分發(fā)揮，將沒有聯(lián)系的線連接起來，使他們存在一定程度的關系；

(3)最后將圖線與輔助線構(gòu)成新圖形.

二、通過在圓中添加輔助線探究其規(guī)律

在圓中添加輔助線的方法主要有以下幾種：

(1)可以根據(jù)圓的垂直平分定理，在圓心的基礎上有弦的垂直線段；

(2)可以根據(jù)圓中的圓心角、圓周角、弧及弦這四者的轉(zhuǎn)換關系在連接圓上的點作輔助線來解決圓中的問題，這也體現(xiàn)了輔助線在圓中的規(guī)律；

(3)當解決有關圓形的問題時，看題目中是否有直徑這個條件，如果有的話就要考慮直徑所對應的圓周角是否是直角這個問題來添加輔助線；

(4)當解決有關圓形問題的時候有切線，可以連接切點的直徑或者半徑，通過兩者垂直的特點來作輔助線.

(5)當解決圓形問題的時候，題目中如果是兩個圓相切，首先就要考慮通過切點來作兩圓的公切線，這樣使弦切角和圓周角之間有所關聯(lián).也可以作這兩個圓的連心線，通過切點和連心線上圓心距與圓半徑的關系來作輔助線；

(6)在解決圓形問題的時候，題目中如果是兩個圓相交的時候，可以通過兩個圓的公共弦來構(gòu)建一個橋梁，使這兩個圓的圓周角與其他的角存在一定的聯(lián)系.

通過以上描述，就可以了解到在圓中及其他幾何圖形中添加輔助線都是有規(guī)律的.學生能夠通過了解輔助線的添加方法以此來在圓中添加輔助線，從而能夠更好地學習數(shù)學，提高解決幾何圖形問題的技巧.以下就舉例說明圓中輔助線的規(guī)律性.

三、利用圓畫輔助線的規(guī)律性

(1)如圖1所示，在解決圓形中弦的問題的時候，數(shù)學老師一般會讓學生由圓心向弦AB作垂線段OC.

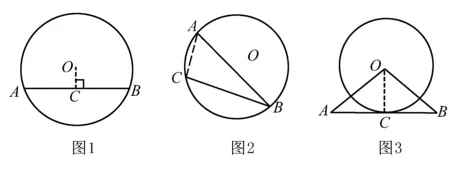
(2)如圖2所示，在圓中有直徑時，連接AC，可得到直徑AB所對的圓周角∠C是直角.

(3)如圖3所示，在AB與圓O切于點C時，過點C作出半徑OC，可得到OC⊥AB.

以上就圓中的弦、直徑、切線，介紹了常用到的輔助線作法.在以后遇到這類數(shù)學問題的時候，都可做同樣的輔助線，那么就可以說這些輔助線存在著一定的規(guī)律性.

四、在初中數(shù)學中添加輔助線的兩種情況

在我國人民解決問題的時候，都是靠著自己的聰明來進行的，當遇到問題但是達不到一定條件的時候，就可以使用輔助線來使其構(gòu)成新的圖形，將題中的各種條件進行集中進行，建立解決問題的橋梁，從而使問題得到解決，這是初中數(shù)學老師教給學生最基本的解決問題策略.其中在初中數(shù)學中添加輔助線可分為兩種情況：

(1)按照數(shù)學定理來添加輔助線.在圓中使兩條線進行延伸，證明兩者相交后的角是直角，輔助線與其中的點和線段之間存在一定的關系，得到的角與輔助線之間也存在一定的關系.

(2)按照圖形來添加輔助線.在幾何圖形中，都有與其相對應的幾何定理，添加輔助線主要是彌補圖形中的不完整性，所以輔助線也可稱為“補圖”.在此過程中還可防止胡亂添加線段，所以添加輔助線也是有一定規(guī)律的.比如：

其一，平行線.在幾何圖形平行線中添加輔助線的時候，其目的是為了使輔助線與這兩條平行線相交.

其二，等腰三角形.在等腰三角形中往往會彌補其不完整性，從一點出發(fā)添加兩條輔助線.當出現(xiàn)平分角或者平行線的時候，可以延長平行線使其與角相交，從而得到等腰三角形.

其三，圓中的圓周角.在圓中的點上添加一個直角圓周角，可以以點為中心，添加一條直徑.

在數(shù)學中添加輔助線的時候，還有初中教師為了方便學生記憶而創(chuàng)作了口訣.盡管有這些方法，在學生遇到幾何問題的時候，還是要認真分析，添加一條科學合理的輔助線，這樣才能避免學生少走彎路，并且可以提高學生的創(chuàng)新思維，提高學生解決問題和思考問題的能力.在學習數(shù)學的過程中，只有多思考、多動腦、多做練習并且對其進行總結(jié)，才能掌握數(shù)學中的規(guī)律，從而解決問題.

G632

B

1008-0333(2016)35-0003-01