裝備保障資源均衡遺傳算法優化與仿真

王建成， 邱 輝， 郭 凱

(1. 裝備學院 裝備指揮系, 北京 101416； 2.裝備學院 研究生管理大隊, 北京 101416； 3.61046部隊)

?

裝備保障資源均衡遺傳算法優化與仿真

王建成1， 邱 輝2, 3， 郭 凱1

(1. 裝備學院 裝備指揮系, 北京 101416； 2.裝備學院 研究生管理大隊, 北京 101416； 3.61046部隊)

合理利用裝備保障資源是組織裝備保障活動的必然要求，科學規劃是裝備保障資源合理利用的基本前提。裝備保障任務工期內對保障資源需求的波動量越小越有利于裝備保障活動的高效組織、實施、管理以及裝備保障效能的提高。資源均衡優化是實現資源需求均衡的重要技術手段。傳統求解資源均衡問題的精確解法和啟發式優化方法在解決這類中大規模問題時難以奏效，帶修復算子的遺傳算法能夠在一定程度上克服這些算法存在的缺點，其有效性通過獲得幾個模擬問題的最優或次最優解得以驗證。

資源均衡；裝備保障；遺傳算法；網絡計劃

裝備保障資源是裝備保障活動的重要物質基礎，裝備保障活動對保障資源需求的波動量越小越有利于裝備保障活動的組織、實施、管理以及裝備保障效能的提高。資源均衡優化是實現資源需求均衡的重要技術途徑[1]和進行裝備保障任務規劃計劃的重要環節，其目標是通過合理安排各道工序，從而盡可能地減少任務工期內對資源使用需求的波動。由于資源均衡優化是NP(Non-deterministic Polynomial)問題，用完全枚舉法求解中規模資源均衡問題時因搜索空間過大而難以獲得問題的最優解。傳統求解這類問題的數學模型包括整數規劃、動態規劃和分支定界法等[2-5]，但均因無法有效解決組合爆炸瓶頸問題而僅能用于求解小規模問題。近年來，遺傳算法(Genetic Algorithms，GA)作為一個全局隨機搜索算法[6-8]，具備有效克服組合爆炸問題的能力，因而被用來求解裝備保障資源優化問題，從而在一定的折中條件下獲得中大規模資源均衡優化問題較為滿意的規劃解。

1 問題描述

裝備保障資源均衡優化問題可以用網絡圖描述。圖1所示為一項裝備保障任務的雙代號網絡，其中有9道工序和6個節點。工序之間具有確定的前導后繼關系，并且每一對節點間的工序數不超過1。(i,j)表示節點i和j之間的一道工序，例如(4, 5)表示工序“G”。所有工序的集合記為W，所有虛工序的集合記為V，工序(i,j)的所有緊前工序的集合記為P(i,j)。

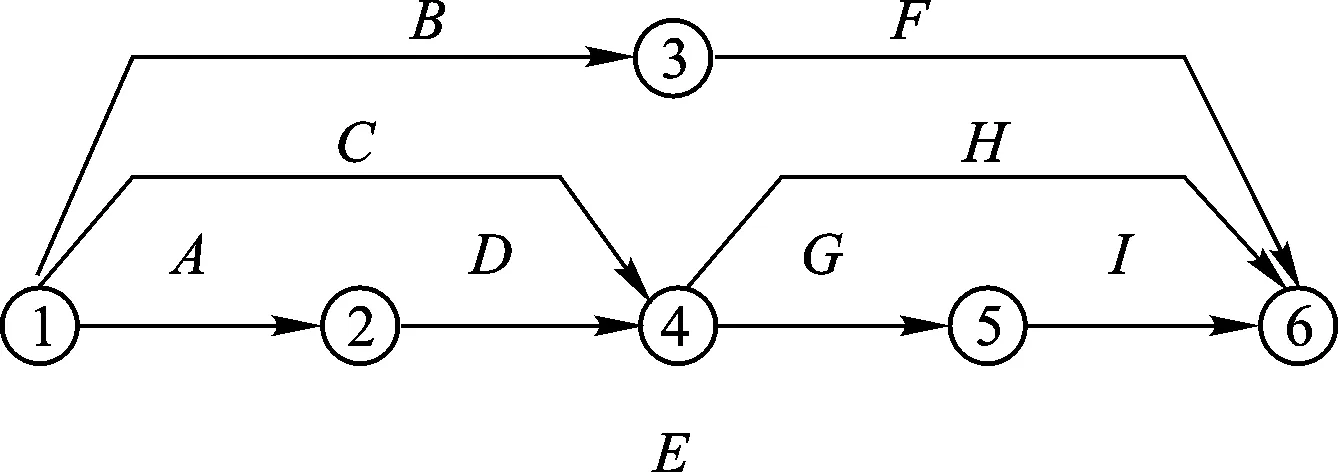
圖1 裝備保障任務雙代號網絡

(1)

(2)

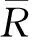
2 帶修復算子的遺傳算法

遺傳算法實際上是通過對決策變量的迭代操作實現的。為獲得GA解，首先必須精心設計染色體結構。一條染色體由N個基因組成，每一個基因對應一個決策變量，表示一道工序的計劃開工時間。簡單遺傳算法的遺傳算子由選擇、交叉和變異算子構成。選擇、交叉和變異算子分別選用賭輪選擇、單點交叉和隨機變異。由于遺傳算子的作用，一條可行的染色體可能退變為非可行的染色體，即非可行解。如果這種情況發生，就要使用修復算子對工序(i,j)的實際開工時間tAS(i,j)進行修復。迭代過程中利用修復準則對一條染色體進行適時檢查，當發現該染色體中某一工序在其所有緊前工序還未結束時開工，即當式(3)所給出的不等式成立時，就表示該染色體為非可行染色體，就應該啟動修復算子進行染色體修復。修復算子強制非法基因值等于工序(i,j)所有緊前工序實際完成時間的最大值。

(3)

遺傳算法是通過不斷產生新的個體、更新當前最優染色體來求解最優化問題的。進化過程中，解的質量由適應度函數進行評價，并且這種評價是染色體選擇的前提。對于工期固定資源規劃問題，工期內資源需求量波動越小，染色體的適應性越強。因此，定義目標函數g(tAS)如式(4)：

(4)

適應度函數f(tAS)可以分別用相對適應度函數和絕對適應度函數定義，分別如式(5)和式(6)所示。

(5)

(6)

3 仿真結果

利用帶修復算子的遺傳算法求解了2個仿真算例：一個小規模問題和一個中規模問題。算法用Matlab語言實現。

3.1 小規模問題

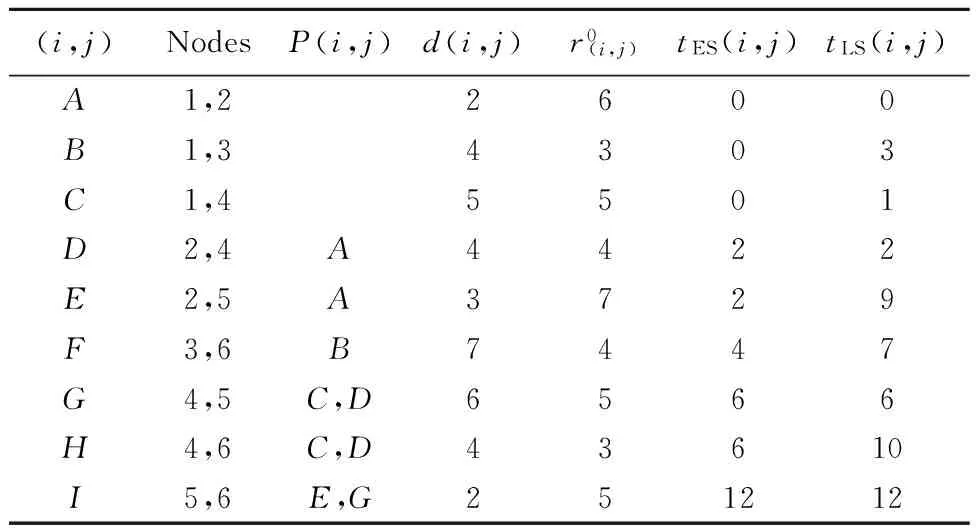
表1 小規模問題參數及CPM結果

精確解。對于該小規模問題，可利用完全枚舉法給出問題的精確解。取所有關鍵工序的實際開工時間為tES(i, j)，將所有非關鍵工序的實際開工時間在區間[tES(i,j) tLS(i, j)]遍歷取值。求解時需要搜索的解的總數為1 280，其中非可行解的個數為480，可行解的個數為800。對這些可行解，通過比較其所對應的任務工期內資源需求量方差的大小選擇出最優解。其中最好的前10個精確解如表2所示。對于最優目標值2.863 7，存在有6個最優解，如表2的前6行所示。對這種最優解不唯一的優化問題，傳統的優化方法很難奏效。

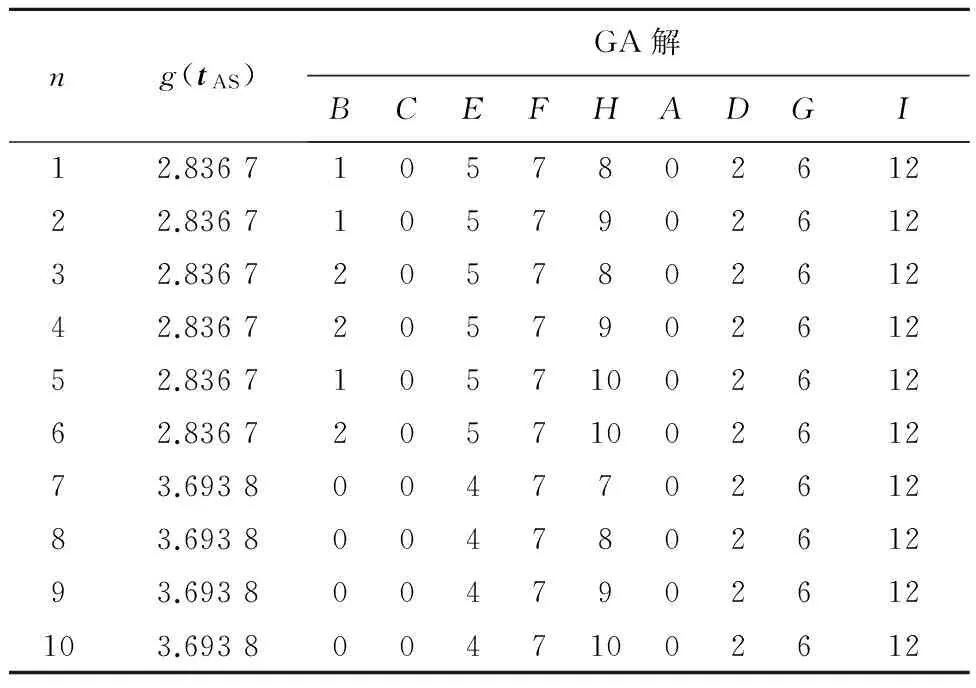
表2 小規模問題前10個最優精確解

GA解。參數popSize=20，chromLen=9，PC=0.65，PM=[0.35 0.25]，maxGen=10。采用相對適應度函數。運行進化程序10次，所得到的GA解列于表3。與精確解對比發現，遺傳算法得到的解中有9個與表2中的最優解一致，這充分表明遺傳算法求解資源均衡優化問題時解的質量。從表3給出的GA解可見，當目標值g(tAS)相同時，遺傳算法可以得到不同的染色體，這充分顯示出遺傳算法在優化這類多極值目標函數時具有隨機收斂到多個全局最優解的優越性能。目標值的進化曲線如圖2所示。顯而易見，當問題的規模較小時，進化過程迅速向精確解收斂。

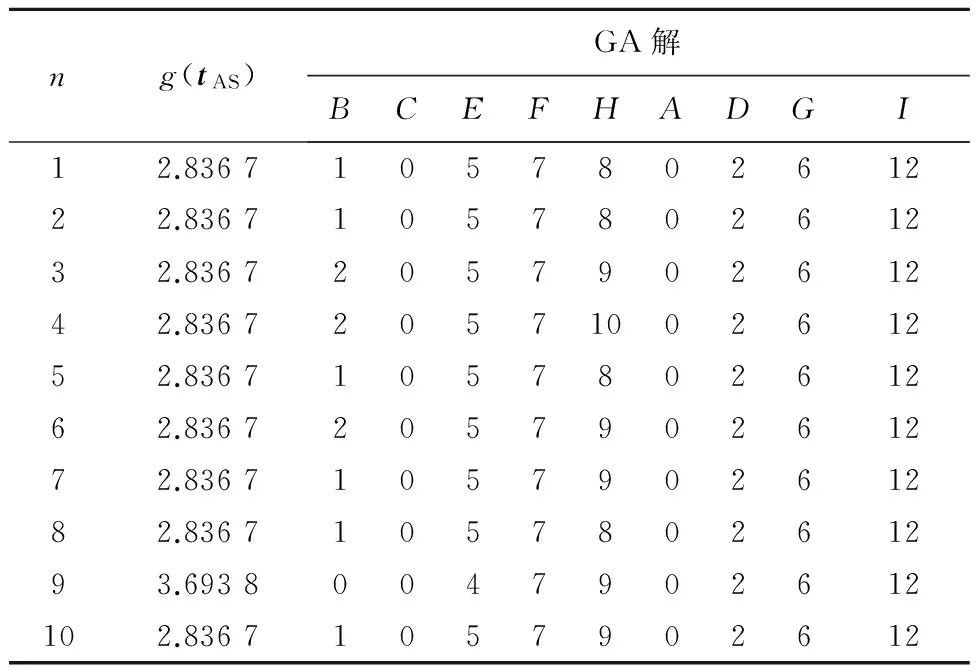
表3 小規模問題10次運行GA解

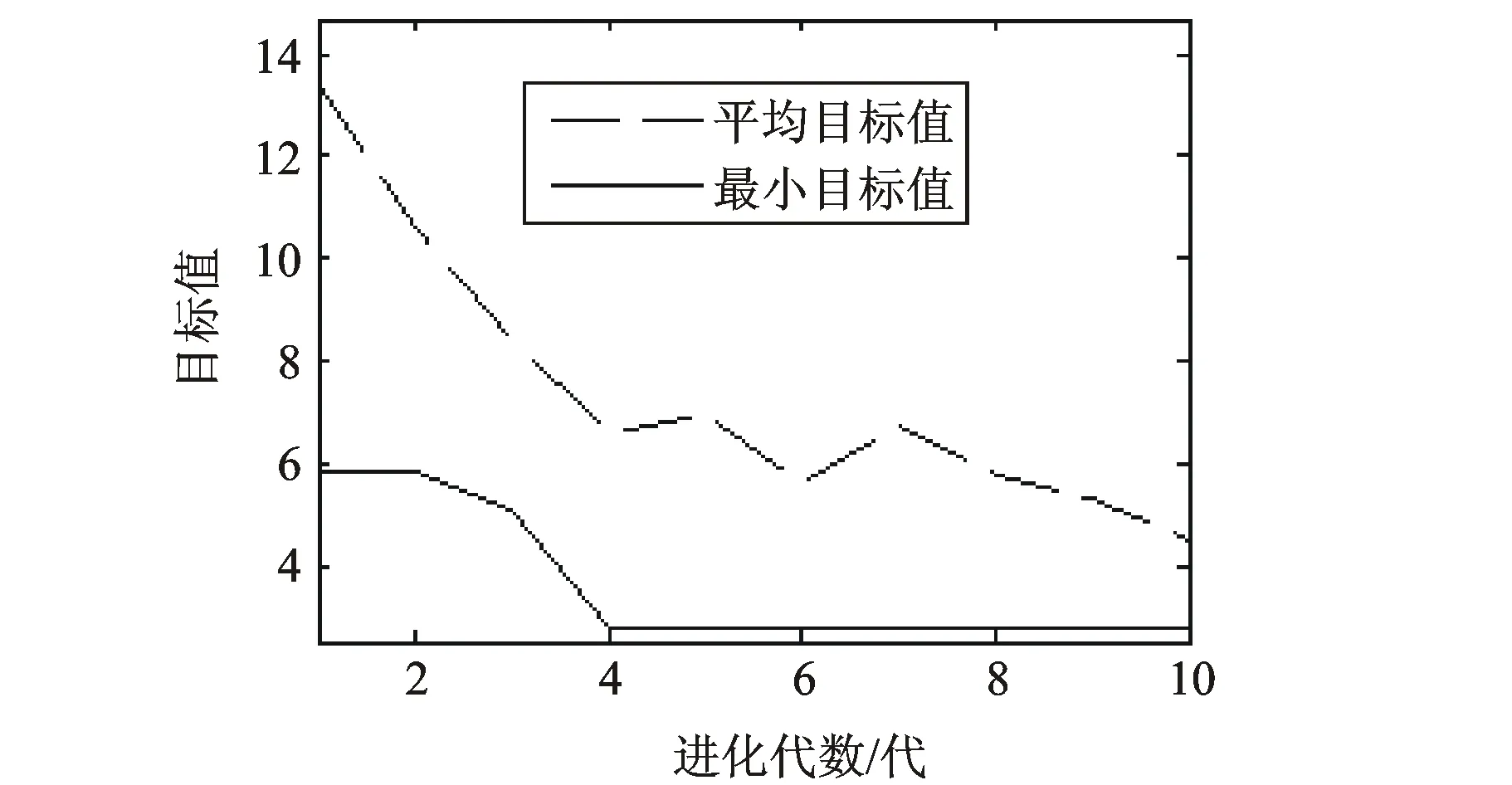
圖2 目標值進化曲線

3.2 中規模問題

圖3 包括17道實工序和12個節點的裝備保障任務等效雙代號網絡

表4 中規模問題參數及CPM結果

圖4 中規模問題各工序規劃的實際開工時間

圖5 中規模問題工期內單位時間資源需求量

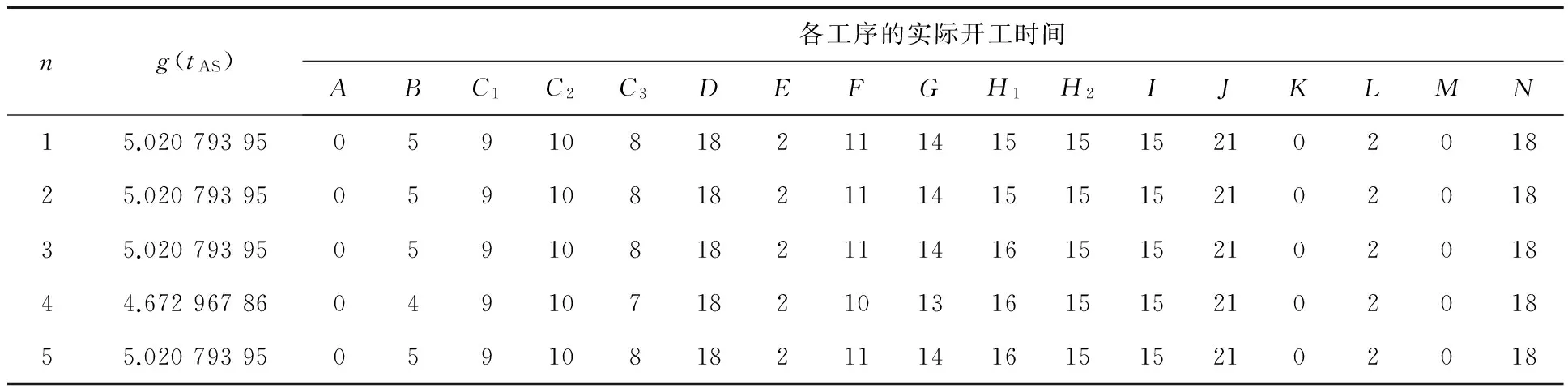
ng(tAS)各工序的實際開工時間ABC1C2C3DEFGH1H2IJKLMN15.020793950591081821114151515210201825.020793950591081821114151515210201835.020793950591081821114161515210201844.672967860491071821013161515210201855.0207939505910818211141615152102018

4 結 束 語

本文研究了基于遺傳算法的中小規模可更新裝備保障資源優化問題，設計了用于修復非可行染色體的修復算子，并通過仿真算例驗證了該方法的有效性。對于中大規模特別是大規模問題的求解以及實現初始種群的多樣性方面，仍需進一步探索。該方法不僅可用于裝備保障活動的規劃計劃，對于其他工作中涉及的同類型資源優化問題具有普遍的適用性。

References)

[1]歐陽紅祥，劉炳勝，李欣.網絡計劃多資源均衡優化遺傳算法[J].武漢理工大學學報(信息與管理工程版)，2013，35(2):180-182.

[2]左傳友.PERT方法優化的導彈技術準備流程[J].海軍航空工程學院學報，2008，23(5):569-572.

[3]LEU S S，YANG C H，HUANG J C.Resource leveling in construction by genetic algorithm-based optimization and its decision support system application [J].Automation in Construction，2000，10(1):27-41.

[4]RIECK J，ZIMMERMANN J，GATHER T.Mixed-integer linear programming for resource leveling problems [J].European Journal of Operational Research，2012，221(1):27-37.

[5]馬登武，郭小威，呂曉峰.基于網絡計劃技術的艦載機航空導彈轉運流程[J].兵工自動化，2010，29(9):48-51.

[6]AHMED B S，NEIL N E.Use of genetic algorithms in resource scheduling of construction projects [J].Journal of Construction Engineering and Management，2004，130(6):869-877.

[7]HEGAZY T.Optimization of resource allocation and leveling using genetic algorithms[J].Journal of Construction Engineering Management，1999，117(3):380-392.

[8]瞿軍，吳文軍，黃全.導彈技術保障資源均衡優化的遺傳算法求解[J].海軍航空工程學院學報，2010，25(2):137-140.

(編輯：李江濤)

Optimization and Simulation of Genetic Algorithm for Equipment Support Resource Equilibrium

WANG Jiancheng1， QIU Hui2,3， GUO Kai1

(1. Department of Equipment Command, Equipment Academy, Beijing 101416, China；2. Department of Graduate Management, Equipment Academy, Beijing 101416, China； 3. 61046 Troops, China)

Reasonable utilization of equipment support resources is necessary when performing equipment support activities and scientific planning is the basic premise for reasonable utilization of the equipment support resource. In the implementation period of equipment support task, the smaller the fluctuation of the support resource demand is, the better the organization, implementation and management of equipment support activities is and this will improve equipment support effectiveness. Resource equilibrium and optimization are key technical approaches to the equilibrium of resource demand. However, traditional precise method and heuristic optimization method are inapplicable to such problems at a mid/large scale. Fortunately, the genetic algorithm with reparative factor can overcome the shortcoming of above algorithms and may be verified in terms of effectiveness by obtaining the optimal or suboptimal solution to several problems of modeling.

resource equilibrium; equipment support; genetic algorithm; network planning

2016-03-02

王建成(1970-)，男，副教授，主要研究方向為裝備保障與指揮。wjianch@sohu.com

E91

2095-3828(2016)06-0133-04

A DOI 10.3783/j.issn.2095-3828.2016.06.025