土體-結構非線性耦合系統動力響應并行計算方法研究

王小慶， 金先龍， 王建煒

(1.上海交通大學 機械系統與振動國家重點實驗室，上海 200240； 2.上海交通大學 機械與動力工程學院，上海 200240)

土體-結構非線性耦合系統動力響應并行計算方法研究

王小慶1,2， 金先龍1,2， 王建煒2

(1.上海交通大學 機械系統與振動國家重點實驗室，上海 200240； 2.上海交通大學 機械與動力工程學院，上海 200240)

針對土體-結構非線性耦合(Soil-Structure Interaction，SSI)系統動力響應數值模擬帶來的大規模計算量問題，提出基于SSI負載均衡及對偶圖理論兩種區域分解算法的并行計算方法。結合傳統的貪婪法及遞歸坐標對分方法，對這四種方法的并行性能進行研究。SSI采用基于對稱罰函數的方法處理，系統方程采用顯式中心差分有限元方法求解。對典型的SSI工程問題動力響應進行并行數值模擬，并對這四種方法的可擴展性進行分析。結果表明：基于SSI負載均衡的并行計算方法，充分考慮土體和結構耦合負載的均衡，并行效率最優，基于對偶圖理論區域分解的方法和遞歸坐標對分方法效率次之，貪婪法并行效率最低；隨核數增加，并行效率下降，需根據實際模型規模合理選擇并行計算核數，獲得最優的并行計算效益；基于罰函數的顯式有限元方法能夠較好的解決SSI動力響應問題。

結構-土體非線性耦合；區域分解；并行計算；動力響應；顯式有限元；對稱罰函數法

土體-結構耦合(Soil-Structure Interaction，SSI)問題廣泛存在于各種工程系統中，如土體-隧道、列車-隧道-土體、土體-高層建筑、土體-橋梁、土體-核島等耦合系統，因而得到學者的廣泛研究[1-4]。隨著問題規模的擴大，并行計算成為解決大型土體-結構耦合系統動力響應的有效手段，各種并行算法成為研究熱點[4-7]，我國超級計算機的蓬勃發展與領先，也為并行計算提供了必需的硬件基礎。

土體-結構耦合系統，就是將土體和所研究結構視為彼此協調工作的整體，考慮結構與土體動力響應的相互作用，進而求解系統方程獲得變形和內力等響應。從研究方法上看，可分為理論研究[8]、實驗研究及數值模擬[9]。三種方法各有優勢，數值模擬技術因其研究周期短、可重復性強、可處理非常復雜的問題，應用越來越廣泛。從研究內容上看，有單獨對各類土體-結構耦合系統特性的研究[10]，有考慮土體-結構耦合的大型工程分析[11-13]，前者的研究最終也是為輔助其在實際工程中得到合理的應用。考慮土體-結構耦合的大型工程數值模擬帶來精細結果的同時，也伴隨著模型自由度及求解方程規模的急劇增加，為加快求解速度，提高計算效率，各種并行計算方法應運而生，YERLI等[4]在分布式計算機上利用子結構法和有限-無限單元法提出土體-結構耦合問題的并行算法，并加以程序實現，通過算例證明了所提并行算法的有效性。GENES等[5-6]利用比例邊界有限元法模擬遠場無限土體，采用有限元法模擬近場土體及結構，在二者基礎上提出土體-結構耦合模型并將其并行化，通過求解現有文獻中的算例，并和文獻中已有的結果進行對比，驗證其模型及并行程序的準確性。MESCHKE等[7]利用有限元法提出隧道機械化掘進中樁-土耦合作用的并行數值模擬方法，并對基于OpenMP的共享內存式及基于MPI的分布內存式并行技術進行對比分析，結果表明基于區域分解的分布式并行計算能夠獲得更好的并行效率。目前針對土體-結構耦合并行計算的研究多是基于不同的數值方法與一些特定應用對象進行，大多未考慮分區優劣對并行效率的影響。

本文提出針對大型土體-結構耦合系統動力學分析的土體-結構耦合負載均衡及基于對偶圖理論區域分解的并行計算方法。土體-結構耦合采用基于對稱罰函數的方法處理，系統方程采用顯式中心差分有限元方法求解。通過工程實例與基于傳統的貪婪法和坐標遞歸對分的并行計算方法進行對比，評價各種方法的并行性能，為類似研究提供借鑒。

1 SSI動力響應問題基本數值方法

1.1 顯式有限元方法

土體-結構耦合系統的動力響應，如地震動響應，列車動載激勵下的響應等，可利用顯式有限元方法求解，耦合系統動力學方程可表示為：

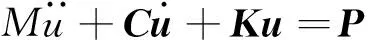
(1)

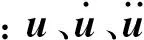
土體-結構耦合動力學問題，因存在接觸而具有高度非線性特點，易采用顯式算法求解式(1)。顯式中心差分法無需組集總體剛度矩陣，當質量和阻尼陣為對角陣時無需矩陣分解和求逆，可節省內存和計算機時，也更適合并行化。利用中心差分在時域內離散：

(2)

(3)

式中:Δtn+1/2=(Δtn+Δtn+1)/2。當0～t時刻節點位移、速度及加速度已知時，利用上述遞推公式可得到整個時域內系統的響應。顯式中心差分法是條件穩定的，穩定時間步長由最小單元特征長度及當前波速決定。

1.2 基于對稱罰函數的SSI算法

土體與結構耦合，存在相互擠壓和滑動等行為[13]，屬邊界非線性問題，接觸算法比節點重合更符合物理實際。研究表明基于對稱罰函數的接觸算法適于土體-結構耦合動力響應問題的處理。

利用基于對稱罰函數的接觸算法處理土體-結構耦合問題，涉及接觸搜索算法和接觸力計算方法兩個方面。接觸搜索可采用基于段的Bucket分類搜索算法，其基本原理是將接觸空間劃分為多個很小的Bucket,然后，根據每個從節點所屬Bucket搜索并確定最近的主段，從而進行接觸判斷。接觸力計算則采用對稱罰函數法，該方法動量守恒準確，易于程序實現。其基本原理是：每一時步檢查各從節點是否穿透由接觸搜索算法確定的主段，若無穿透，則不作處理；若發生穿透，則在從節點與被穿透主段之間引入界面法向接觸力，如式(4)。從節點處理完成后，對各主節點進行一遍相同的操作。

fi=lλkiηi

(4)

式中:l為判斷是否穿透的參數，λ為罰函數因子，ki為罰函數剛度，ηi為節點i的穿透量。接觸面的摩擦力利用經典Coulomb摩擦理論計算。

2 SSI動力響應問題并行計算方法

2.1 區域分解技術

區域分解是實現并行計算的必要前處理，其思想最早由Schwarz提出，隨著高性能計算的發展，區域分解技術得到廣泛研究和應用。其數學描述為，假設計算區域為Ω，則子區域Pi?Ω,i=1,…,NP的集合P={Pi}i=1,…,NP為Ω的一個區域分解，當：

(5)

區域分解的邊界為集合：

(6)

區域分解技術可分為重疊和非重疊區域分解兩類，其中非重疊區域分解更適合并行計算體系結構,易于處理大型工程的并行數值分析[14]。有限元網格的非重疊區域分解有兩種即基于節點的區域分解和基于單元的區域分解，分別對應于圖分區中對偶圖分解和節點圖分解，如圖1。基于節點的區域分解(圖1(a))，每個單元有唯一分區歸屬，相鄰分區的共享節點則復制并分配到所有共享分區，各鄰接分區間通過共享節點通信；基于單元的區域分解(圖1(b))，每個節點有唯一分區歸屬，相鄰分區的共享單元被復制并分配到所有共享分區，各鄰接分區通過共享單元通信。在不考慮接觸等額外計算負載時，顯式有限元動力分析的時間基本消耗在單元計算上，如內力更新等，同時相鄰分區間共享節點的復制更加容易，因而在土體-結構耦合動力分析中采用基于節點的非重疊區域分解技術。

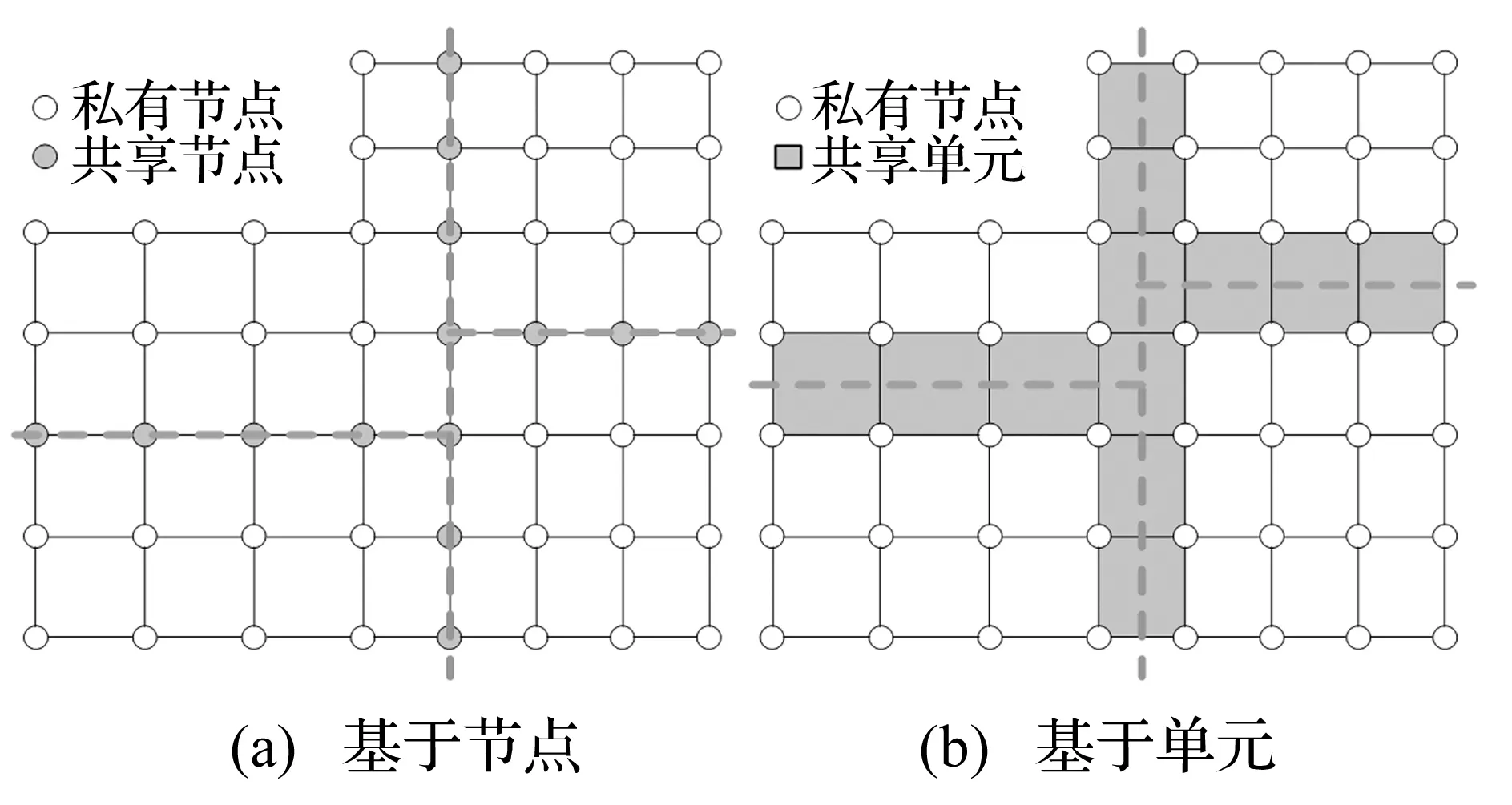
圖1 有限元網格非重疊區域分解Fig.1 Non-overlapping domain decomposition of FE mesh

分區結果的優劣直接關系后續并行求解的效率，通常可通過兩方面評判即各個子區域的計算負載是否均衡以及各分區間的通信消耗及整體通信消耗是否最小[15]。良好的負載均衡減少或者消除各處理器核的空閑等待時間，盡量少的通信可以降低通信在整個并行計算中所占時間比例，二者都可以提高并行計算效率。

2.2 區域分解方法

區域分解的實現可采用多種方法，如基于貪婪法的區域分解(Greedy Domain Decomposition,GDD)、遞歸坐標對分方法(Recursive Coordinate Bisection,RCB)、最小和最大極慣性軸方法，遞歸譜對分方法等，此處重點介紹GDD方法、RCB方法及本文提出的土體-結構耦合負載均衡區域分解方法(Soil-Structure Interaction Balanced Domain Decomposition,SSIB)和基于對偶圖的區域分解方法(Dual-Graph Based Domain Decomposition,DGB)。

貪婪算法是遞歸利用當前局部最優解,逐步得到或者逼近全局最優解的一種求解最優化問題的策略。基于貪婪法的區域分解GDD，即是利用貪婪算法的理念完成有限元網格等的區域分解。定義節點的權重為該節點所連接的單元數；模型總單元數為Nt；目標分區數為Np。GDD的貪婪策略為每次選擇當前最小權重的節點所連接的所有單元為初始分區，然后將已有單元的鄰接單元擴展進分區，遞歸執行，直到分區內單元數達到Nt/Np，然后進行下一個分區。GDD的基本執行流程為：首先，選擇上一分區Pi-1邊界中權重最小的節點ni，初始整體網格為分區P0；接著，將和該節點所有相鄰的未標記的單元劃歸該分區Pi；然后，對分區Pi中所有已有的單元ek，遞歸執行：①標記ek，②將組成ek的所有節點的權重減1，③將所有和ek鄰接的未標記的單元劃給分區Pi；最后，當分區Pi單元數達到Nt/Np，完成該分區，并進入下一分區，直到分區完成。GDD方法原理簡單，執行高效，但局限于貪婪法的局部最優特點，其分區難以達到全局最優，對于土體-結構耦合問題，并不能保證分區間土體-結構耦合負載的均衡。

RCB方法由BERGER和BOKHARI在1987年提出，其分區基本原理為：首先，判斷模型在三個坐標方向的長度，沿垂直于最長坐標方向將模型一分為二，被分割成的兩部分分別包含網格總數的一半；然后，判斷新模型在三個坐標方向的長度，仍然沿垂直于最長坐標方向將新模型一分為二；最后，按照上面的策略，依次將模型分割直到滿足分割收斂條件。RCB方法簡單高效，無需對整體模型進行重新分區即能方便進行局部負載重平衡。但對幾何形狀復雜的區域，RCB方法會產生不連續分區和極小分區，影響后續并行計算效率。同時，RCB方法僅根據幾何模型信息進行分區，未考慮模型的載荷分布和接觸位置，對于土體-結構耦合的大型結構動力響應問題，由于存在大量接觸搜索計算，該方法并不能保證各子區域計算負載的均衡。

針對土體-結構耦合問題的特點，本文提出基于耦合負載均衡的區域分解方法SSIB，其基本思想是保證各區域土體-結構耦合計算負載均衡，從而使得各子區域總計算負載達到均衡。SSIB分區基本原理為：首先搜索所有參與土體-結構耦合的接觸運算單元及鄰接單元；接著根據參與并行計算的核數將所搜索的單元均分，并劃定區域邊界；然后，根據分區邊界，將邊界共享節點復制，并分配到各共享分區；進而，將其余未參與耦合的單元按照空間坐標位置分布到對應子區域中，直到滿足分割收斂條件；最后將各分區模型導入求解器進行并行計算。SSIB方法能在保證各子區域單元數目基本相同的前提下，將需要大量計算資源的土體-結構耦合運算平均分配，保證各子區域總體負載均衡。

基于圖理論的區域分解，能夠處理任意復雜的模型，同時易于并行化，在大規模并行有限元前處理中應用愈加廣泛。本文提出基于對偶圖的區域分解方法DGB，其基本原理為：首先將有限元模型轉換為相應的無向對偶圖；然后將生成的對偶圖利用圖分區理論進行區域分解，本文采用K-路圖劃分算法[16]；最后將對偶圖分區結果映射還原為有限元網格的分區。圖2為有限元網格與其相應對偶圖的映射關系。對偶圖在程序中利用在稀疏圖領域應用廣泛的CSR (Compressed Storage)格式存儲，CSR利用兩個數組Index和Adjac存儲圖的鄰接信息，Index數組存儲每個頂點的開始和終了地址索引，Adjac數組存儲每個頂點的鄰接頂點，對于任意頂點，就可以根據Index中的地址索引在Adjac中找到其所有鄰接頂點。

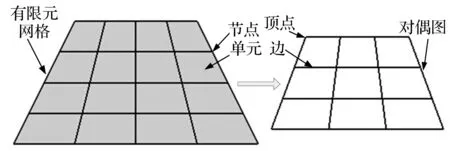
圖2 有限元網格及其對偶圖Fig.2 FE mesh and itscorresponding dual-graph

2.3 基于區域分解的并行計算流程

利用Fortran語言結合MPI函數庫，實現所述區域分解方法的程序化，所開發程序可以讀入有限元輸入文件完成區域分解，輸出結果可以被后續求解程序讀入，完成并行計算求解。利用顯式求解技術以及各種區域分解方法，可以得到土體-結構耦合問題動力響應并行求解流程，如圖3所示。

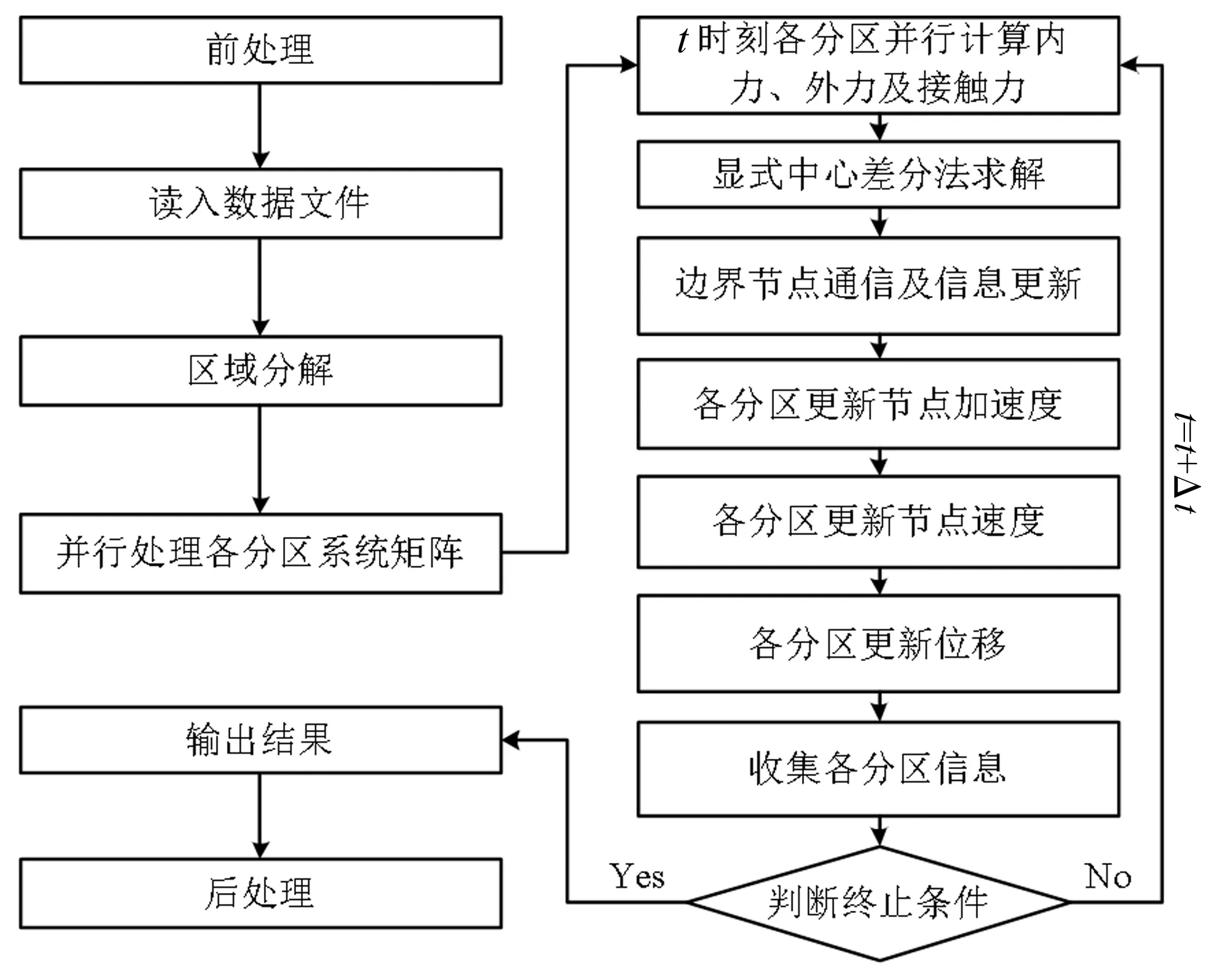
圖3 基于區域分解的顯式有限元并行計算流程Fig.3 Flow chart of the domain decomposition based parallel explicit FE solving procedure

本文研究工作并行計算環境為曙光5000A超級計算機(top500排名360，2014年11月)，其基本參數如表1所示。計算軟件為優化的MPP版本LS-DYNA，采用所開發的區域分解程序對涉及土體-結構耦合的動力學有限元模型進行分區，然后進行并行計算，評價各種區域分解方法對并行性能的影響。

表1 曙光5000A系統信息Tab.1 The system information of Dawning 5000A

本文采用強擴展性評價各種方法的并行性能，評價指標為加速比和并行效率，如式(7)所示，其中Sap為實際加速比，ts為單個核計算時耗費時間，tm為采用多核計算時耗費時間；Em為并行效率，Sip為理想加速比，對于起始為單核的情況下，Sip即為多核時的核數。

(7)

3 工程應用實例

3.1 隧道地震動響應分析

隧道地震響應中，隧道襯砌與周圍土體的作用屬于典型的土體-結構耦合問題。本文以上海某輸水隧道為例，利用并行計算方法分析其在地震動作用下的動力響應。圖4為有限元數值模型，隧道襯砌采用厚殼單元離散，土體采用8節點六面體單元模擬，模型節點總數約為190萬。

有限元模型中土體-結構耦合采用前述基于對稱罰函數的接觸算法，土體-結構耦合情況如圖4(c)所示，具體數值分析中土體和結構接觸面分別設置為主和從接觸面，通過調整接觸控制參數，主要包括接觸剛度計算算法、接觸摩擦參數、罰因子、黏性接觸阻尼及最大穿透量等，提高土體結構接觸模擬的準確性。輸水隧道內水采用附加質量法模擬。土體模型根據實際勘測資料分為10層，基巖深度為300 m，土體本構采用Biot滯回材料模型，隧道周圍土層的力學參數如表2所示，其中ρ為密度，E為彈性模量，ν為泊松比，γ為阻尼比，H為卓越頻率，w為剪切波速。采用PML人工邊界層，模擬無限區域，消除邊界截斷誤差。地震激勵采用50年超越概率10%的基巖加速度時程，時程曲線根據隧道場地基巖反應譜等基巖地震動參數擬合而成，并按照峰值加速度(PGA)0.1 g進行調幅處理。地震動采用一致激勵方式加載。

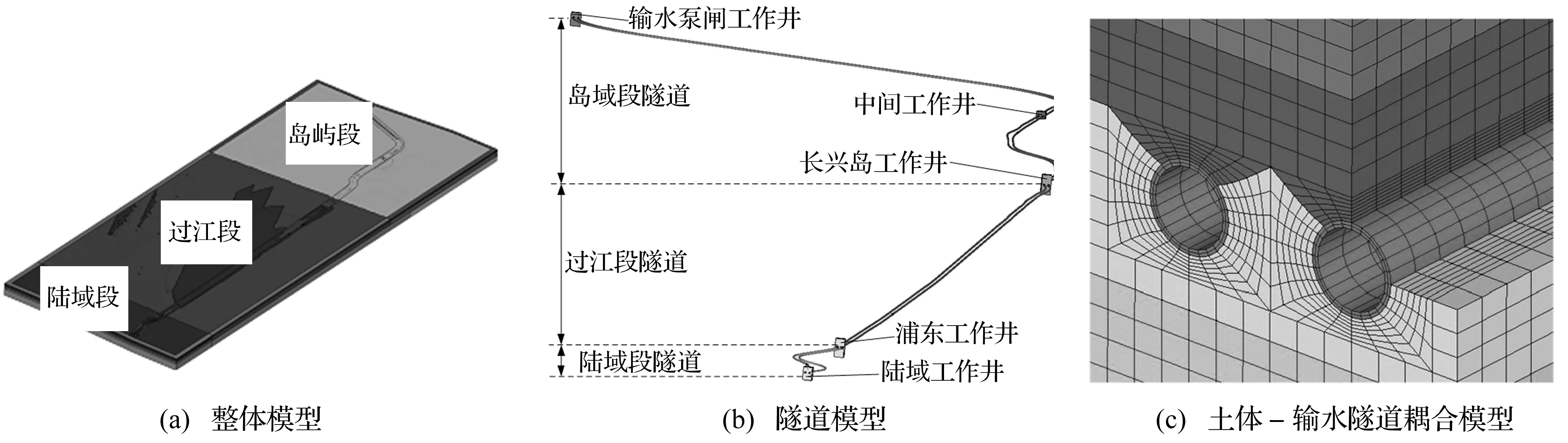
圖4 隧道地震動響應有限元數值模型Fig.4 FE numerical modelfor seismic response of tunnel

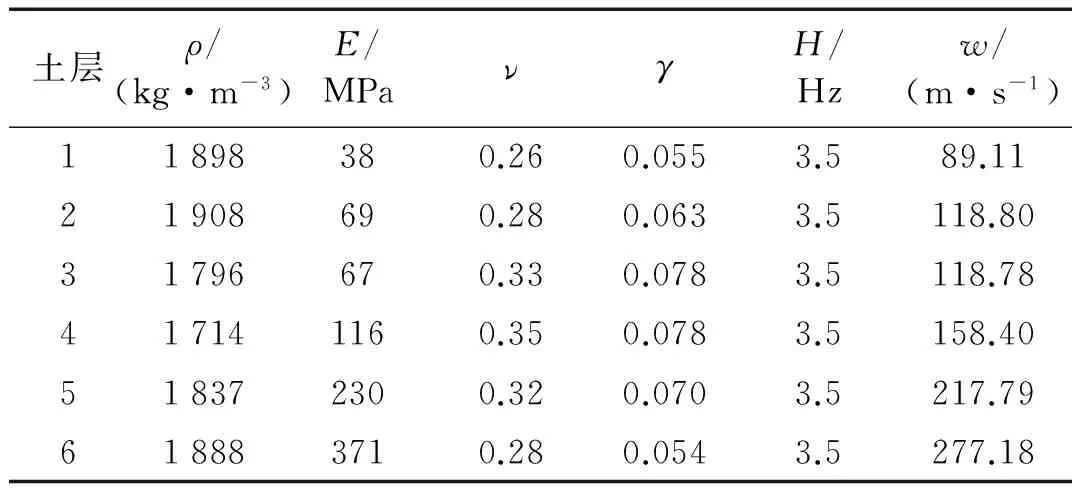
土層ρ/(kg·m-3)E/MPaνγH/Hzw/(m·s-1)11898380.260.0553.589.1121908690.280.0633.5118.8031796670.330.0783.5118.78417141160.350.0783.5158.40518372300.320.0703.5217.79618883710.280.0543.5277.18

圖5為地震激勵下，隧道某斷面直徑變化時程曲線，可以看到隧道截面呈現水平和豎直變化大小基本相同，符號相反的變化規律，這表明隧道呈現類橢圓變形，由圖5可知最大變形大約為1.2E-003，符合上海市《地基基礎設計規范》中隧道襯砌直徑變化的要求，表明隧道結構地震作用下，直徑變化處于安全范圍內。

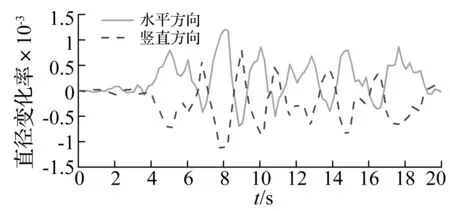
圖5 典型斷面直徑變化率Fig.5 Diameter change rate of a typical section

圖6為采用不同的區域分解方法得到的16分區拓撲結構圖。可以看到，各種區域分解方法得到的分區拓撲不盡相同，GDD方法拓撲較不均勻，DGB方法產生較均勻的不規則分區，RCB方法沿兩個方向進行遞歸對分，而SSIB方法基本沿隧道長度方向分割，其根據土體-結構耦合沿空間分布情況進行區域分解，保證參與土體-結構耦合單元在各子區域的平均分布。

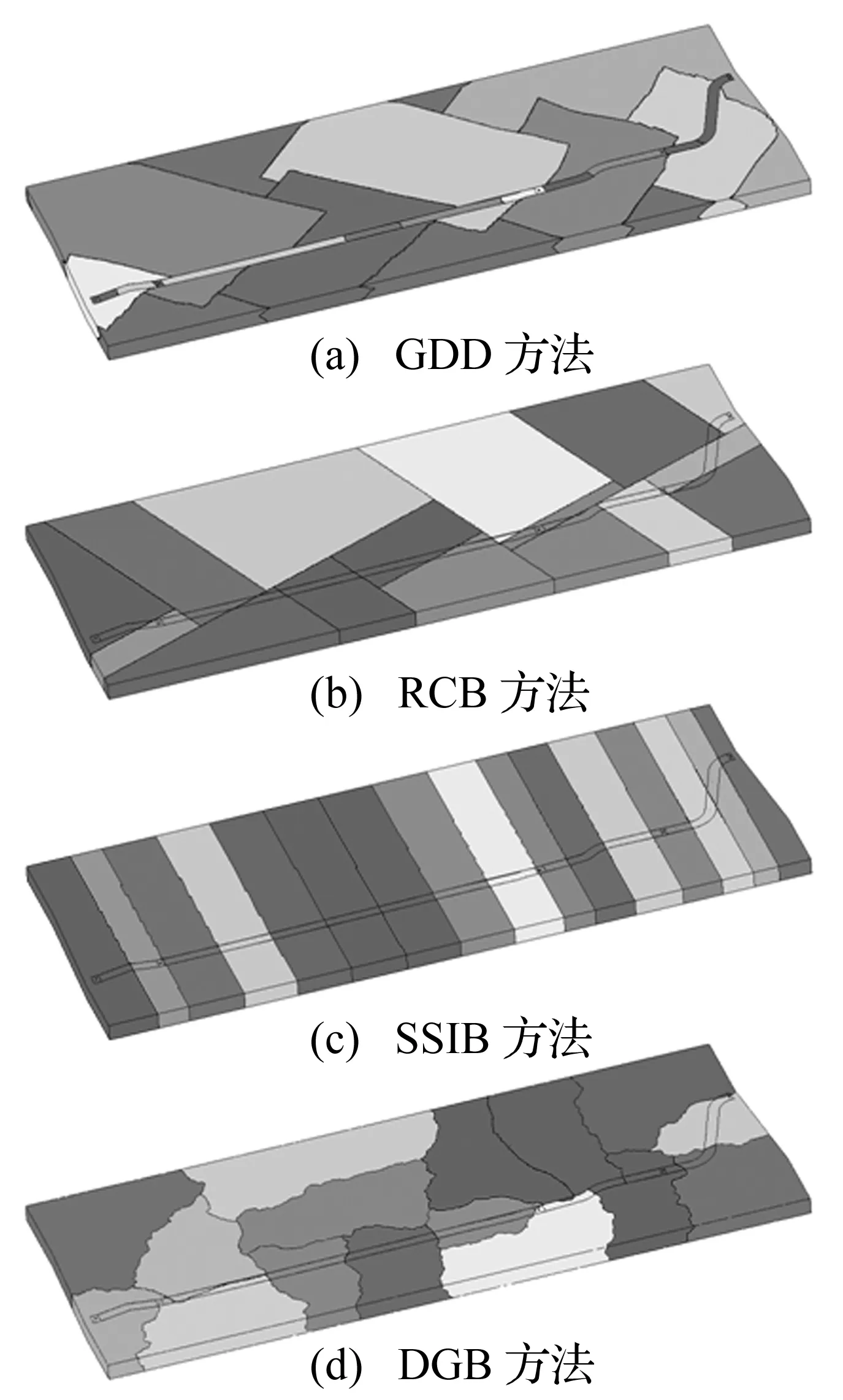
圖6 土體-隧道耦合模型16分區拓撲Fig.6 Topology of 16 partitions for the soil-tunnel coupling model

圖7給出了四種分區方法的加速比和并行效率的對比。由圖7(a)可見，在相同核數時，SSIB方法加速比最優，最接近理想加速比，DGB及RCB方法次之，GDD方法加速比最小。隨著核數的增加，四種分區方法的差異也愈顯著，在32核時，SSIB和DGB表現出較明顯的高加速比。相應地由圖7(b)可以看到，SSIB方法并行效率最高，DGB和RCB方法次之，GDD方法最差，可見考慮土體-結構耦合對并行性能的影響。四種方法的并行效率，均隨核數的增加而降低，主要由于模型規模和拓撲的原因，隨著核數的進一步提升，各分區間通信時間將增加，核數增加帶來的并行效率的提升被增加的通信時間所抵消，因而進行并行計算時需要根據模型具體情況合理選擇并行核數。

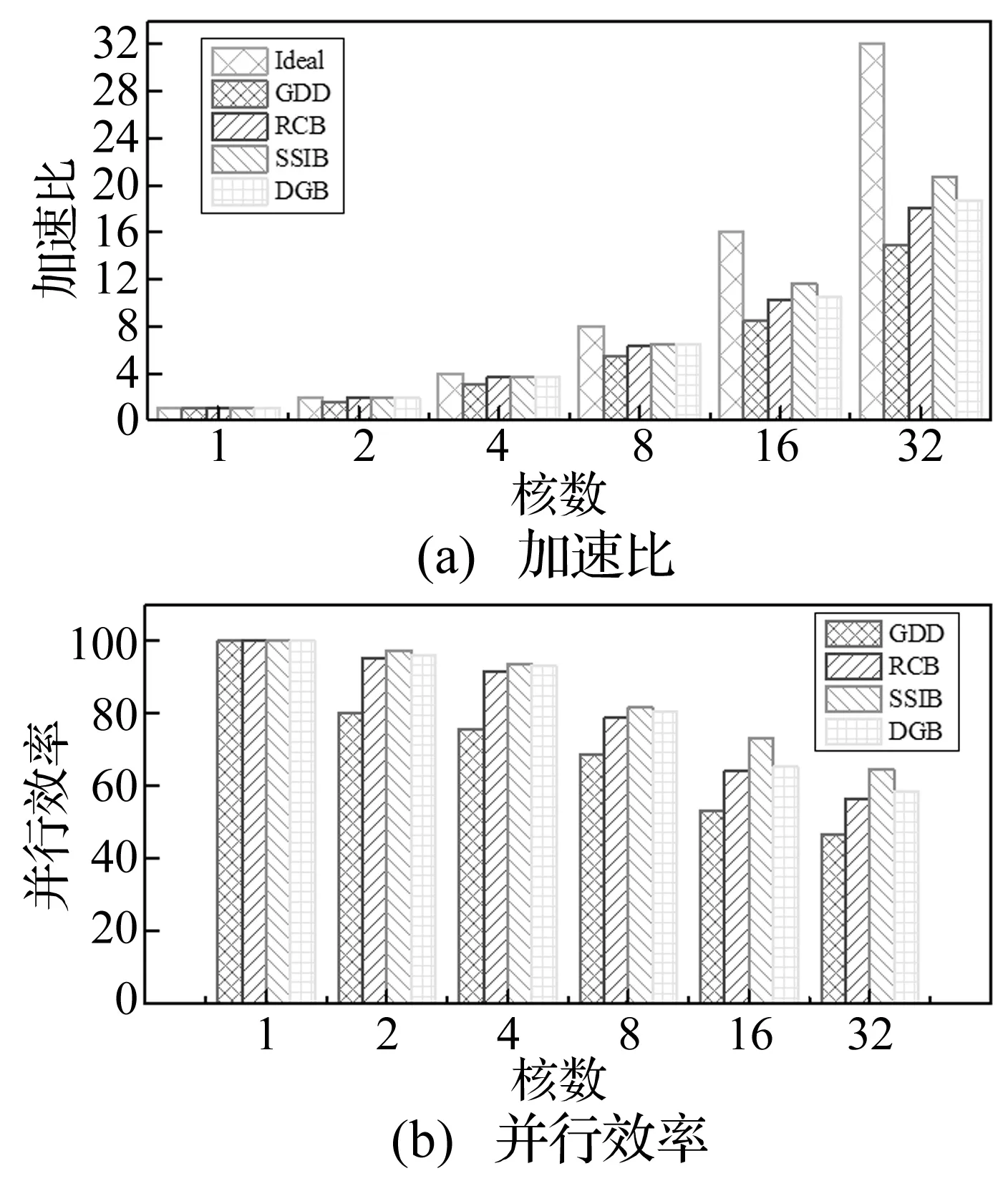
圖7 不同分區方法加速比和并行效率對比Fig.7 Comparison of speed-up and parallel efficiency using different domain decomposition method

3.2 車-隧耦合動態響應分析

車-隧耦合振動分析中也涉及到土體-結構耦合問題。以上海某地鐵隧道為實例，研究各種區域分解方法的并行性能。根據設計資料和地質勘測資料建立車-隧-土體耦合的三維有限元模型，模型節點數大約90萬。該隧道為雙管隧道，中間設置橫向聯絡通道，圖8為有限元數值模型。

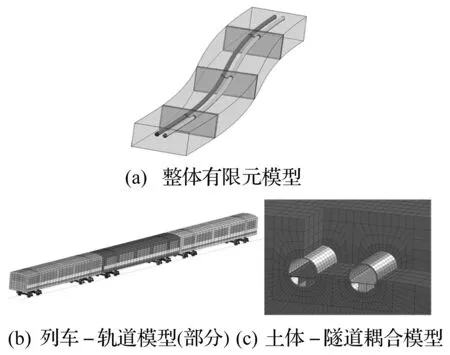
圖8 車-隧-土體動態耦合有限元數值模型Fig.8 Train-tunnel-soil dynamic coupling FE numerical model

土體-隧道耦合采用基于對稱罰函數的土體-結構耦合算法，如圖8(c)為土體-結構耦合模型，土體接觸面設為主接觸面，隧道接觸面設為從面，同時根據土體和結構的相對尺寸及材料屬性，選擇最優接觸控制參數，從而準確模擬土體和隧道的耦合作用。模型采用分層土體(5層)，并利用D-P彈塑性本構模型模擬土體非線性特性，關鍵土層物理力學參數如表3所示，其中ρ為密度，E為彈性模量，ν為泊松比，C為內黏聚力，φ為內摩擦角。采用黏彈性人工邊界模擬無限區域。列車采用10節編組，根據實際幾何信息，采用剛柔耦合方式(車廂采用剛體模擬，懸架系統等采用柔性體模擬)建立有限元模型圖8(b)。軌道不平順采用美國六號軌道不平順譜模型。列車與軌道以接觸方式實現動態耦合。公路車道載荷根據《公路隧道設計規范》施加。

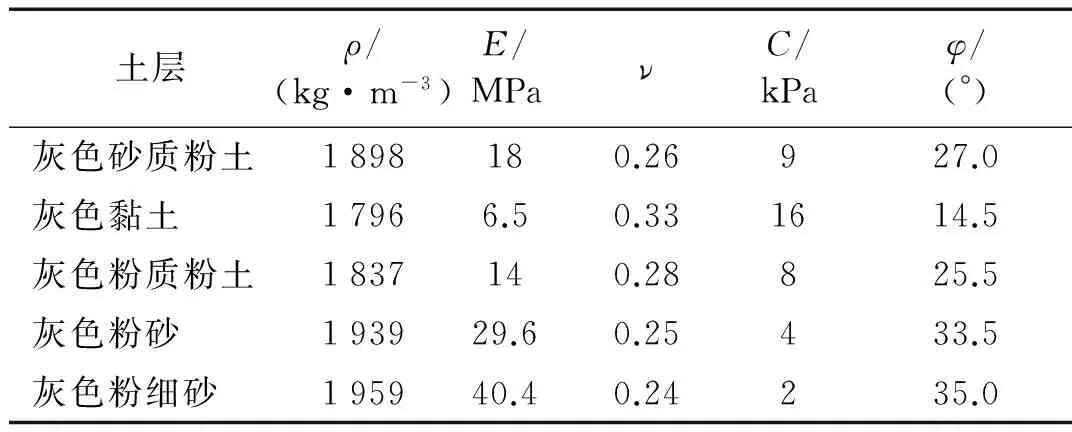
表3 關鍵土層力學參數Tab.3 Mechanic parameters for key soil strata

模擬中首先采用動力松弛方法獲得靜應力場，并將其作為動力分析的初始條件，然后軌道列車以90 km/h的速度勻速由外部駛入并通過隧道。圖9為列車經過時隧道某典型斷面拱頂和拱底的沉降曲線，可見車輛經過時測點位移發生瞬時局部變化，引起隧道局部襯砌約1 mm的沉降，車輛經過之后襯砌位移基本恢復到之前的狀態。圖10為列車經過時某斷面的環向應力變化情況，可見列車經過時引起該斷面極值約0.13 MPa的附加應力。由于10節車廂共20個懸架結構，其中中間18個懸架兩兩在一起，因此軌道車輛經過時，應引起襯砌結構最大主應力約11次較明顯的震蕩，由圖10可明顯看出最大應力出現了11次峰值，這與定性分析相符。

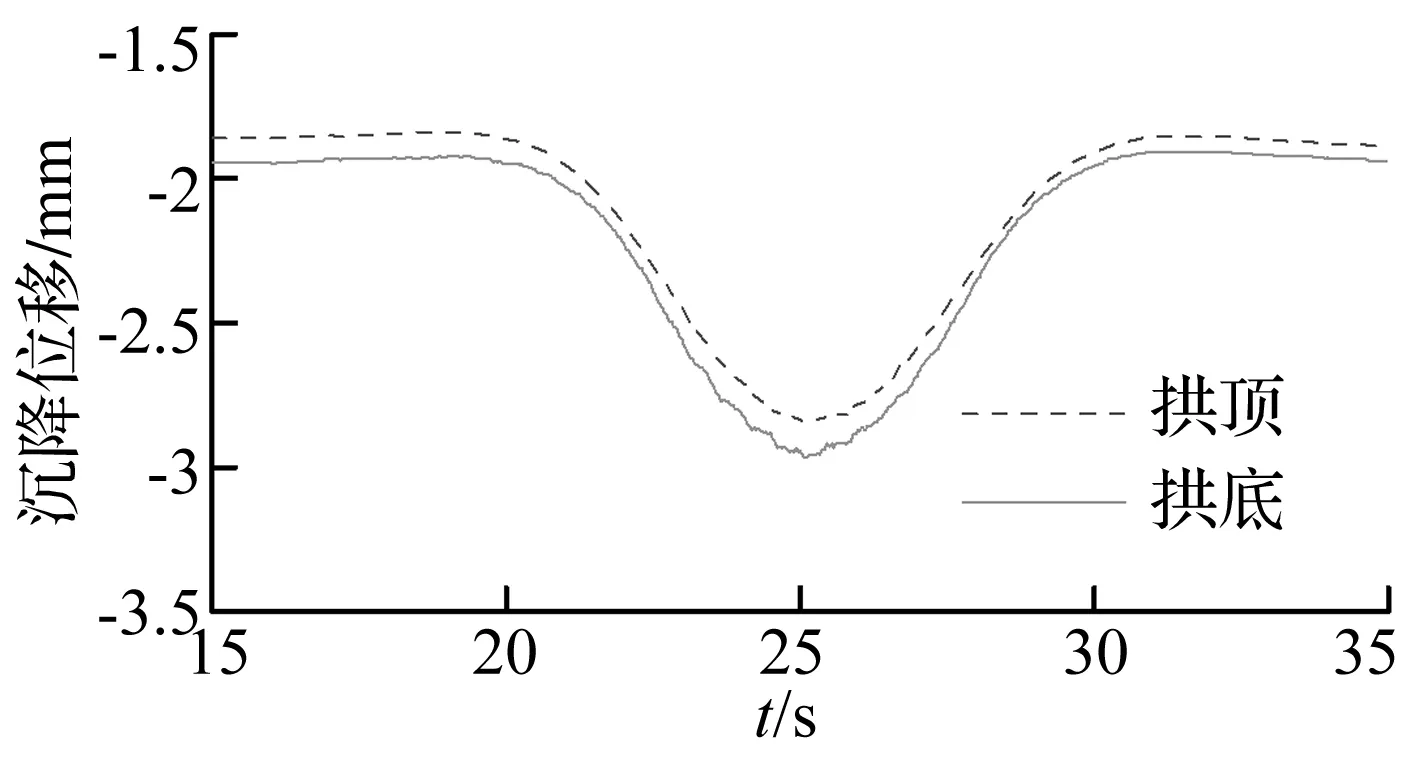
圖9 斷面沉降時程曲線Fig.9 Time history of the subsidence of a cross-section

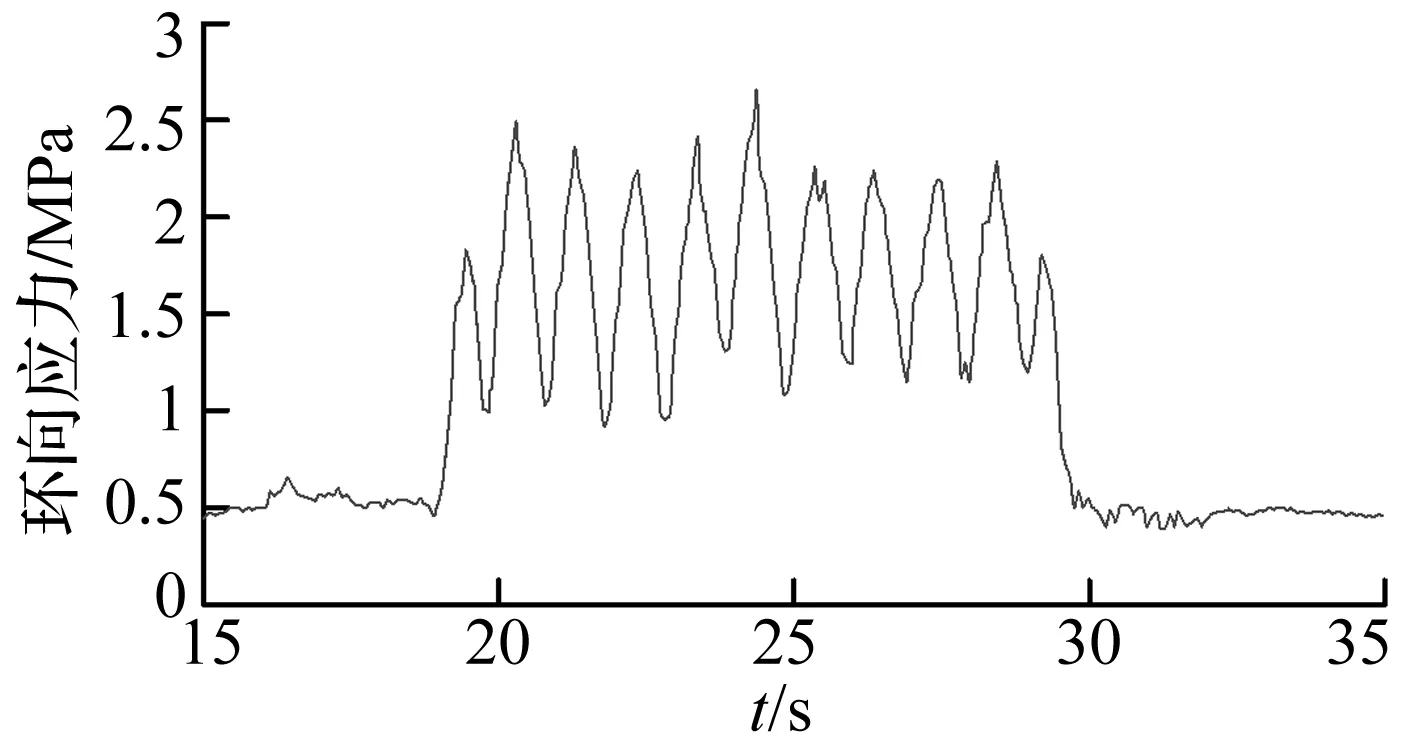
圖10 斷面環向應力時程曲線Fig.10 Time history of the hoop stress of a cross-section

圖11給出了32分區時不同分區方法產生的分區拓撲結構。和實例3.1類似，GDD的拓撲呈現不均勻的不規則分布，DGB的拓撲呈現較均勻的不規則分布，同時DGB和RCB方法呈現相似分區拓撲；RCB每次對分均沿模型最長軸方向，不考慮接觸負載分布，列車模型全部被分到一個子區域中，軌道與列車的接觸計算集中于一個區域內；SSIB方法仍然根據土體-結構耦合的分布情況將其均勻分部到各子區域，同時列車與隧道的耦合也均分到了相鄰幾個分區，使得總體計算量分配更加均衡。

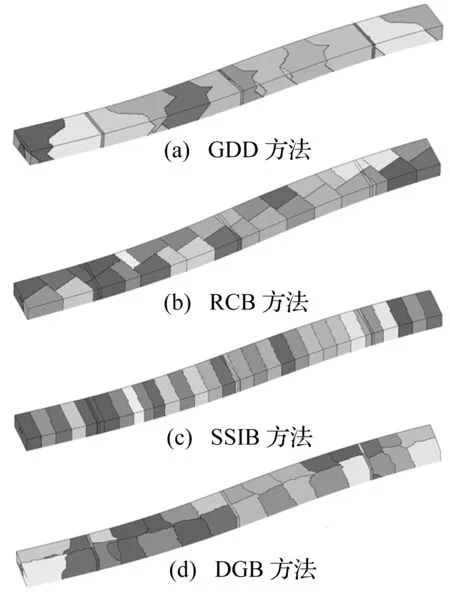
圖11 列車-隧道-土體耦合模型32分區拓撲Fig.11 Topology of 32 partitions for the train-tunnel-soil coupling model

圖12為四種不同方法的加速比和并行效率。由圖12(a)可見，四種方法的加速比呈現非線性變化，并逐漸遠離相應的理想加速比，ISSB方法在不同核數時均呈現較高的加速比，DGB和RCB方法次之，GDD方法加速比最小，并且這種趨勢隨著核數的增加而愈明顯，此外DGB和RCB方法的加速比比較接近。相應地，圖12(b)中，并行效率由高到低依次為SSIB、DGB、RCB和GDD，同時可以看到四種方法的并行效率曲線的斜率逐漸變小，這也表明了隨著核數的增加，由于通信時間在總計算時間中所占比例的增加，而導致并行效率的逐漸降低。該實例的加速比和并行效率變化規律與實例3.1類似，這表明了本文所提出的基于土體-結構耦合的負載均衡方法SSIB和基于對偶圖區域分解方法DGB的有效性。相比于圖7隧道地震動響應的加速比和并行效率。列車-隧道耦合動力響應的相應加速比和并行效率更高，這是因為該模型中還存在車輛和隧道的耦合接觸，其分布與土體-結構耦合分布方向一致，采用SSIB方法也同時保證了車-隧耦合負載的均衡。

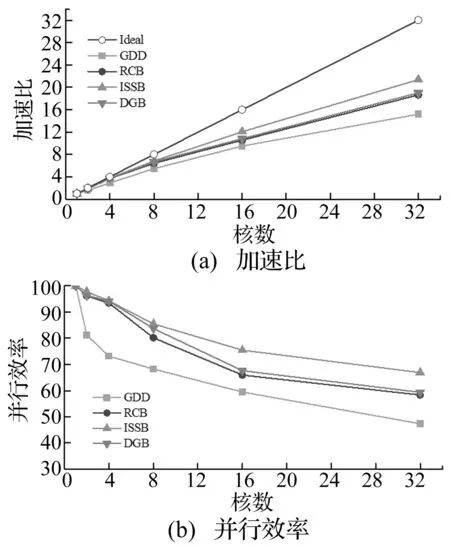
圖12 不同分區方法加速比和并行效率曲線Fig.12 Curves of speed-up and parallel efficiency using different domain decomposition method

4 結 論

對于含有大量土體-結構耦合系統的動力響應數值模擬，并行計算應用越來越多。本文針對此問題提出并程序實現了基于土體-結構耦合負載均衡SSIB及基于對偶圖理論區域分解DGB的并行計算方法。通過實例結合遞歸坐標對分法RCB和貪婪法GDD，對這四種并行方法的并行性能進行了研究，結果表明：

(1)SSIB方法充分考慮土體-結構耦合單元負載的均衡并行效率最優；

(2)DGB方法和RCB方法，雖未直接指定SSI負載的均衡，但其分區拓撲顯示大部分子區域均有一定的SSI運算單元，其并行效率次之；同時利用DGB方法分區時保證切邊最少，從而最大限度的降低通信量，其并行效率較優于RCB方法；

(3)GDD方法負載分配最不均勻，其并行效率最差；

(4)隨核數的增多，分區間通信量增加，并行效率下降，需要根據問題規模合理選擇并行計算核數，獲得最優的并行計算效益。

(5)通過基于罰函數的顯式有限元方法實現了兩類土體-結構耦合問題動力響應的數值模擬，表明該方法能夠較好的處理這兩類問題。

未來的研究工作將考慮引入土體-結構耦合負載均衡系數，對基于圖理論區域分解的并行計算方法進行改進，充分利用其界面通信量小的優勢，通過調整土體-結構耦合負載均衡系數使得其在各子區域負載均衡化，從而獲得更好的并行效率。

[1] LOU M, WANG H, CHEN X, et al. Structure-soil-structure interaction:literature review[J]. Soil Dynamics and Earthquake Engineering, 2011, 31(12): 1724-1731.

[2] 劉毅, 薛素鐸, 李雄彥. 土-結構相互作用下網架結構動力性能研究[J]. 振動與沖擊, 2014, 33(10): 22-28. LIU Yi, XUE Suduo, LI Xiongyan. Grid structure dynamic performance analysis considering soil-structure interaction [J]. Journal of Vibration and Shock, 2014, 33(10): 22-28.

[3] VASILEV G, PARVANOVA S, DINEVA P, et al. Soil-structure interaction using BEM-FEM coupling through ANSYS software package[J]. Soil Dynamics and Earthquake Engineering, 2015, 70: 104-117.

[4] YERLI H R, KACIN S, KOCAK S. A parallel finite-infinite element model for two-dimensional soil-structure interaction problems[J]. Soil Dynamics and Earthquake Engineering, 2003, 23(4): 249-253.

[5] GENES M C, KOCAK S. A combined finite element based soil-structure interaction model for large-scale systems and applications on parallel platforms[J]. Engineering Structures, 2002, 24(9): 1119-1131.

[6] GENES M C. Dynamic analysis of large-scale SSI systems for layered unbounded media via a parallelized coupled finite-element/ boundary-element/scaled boundary finite-element model[J]. Engineering Analysis with Boundary Elements, 2012, 36(5): 845-857.

[8] 鄒立華, 方雷慶. 考慮樁-土-結構相互作用的結構振動控制研究[J]. 振動與沖擊, 2010, 29(11): 100-104.

ZOU Lihua, FANG Leiqing. Structural vibration control considering pile-soil-structure dynamic interaction[J]. Journal of Vibration and Shock, 2010, 29(11): 100-104.

[9] ABATE G, MASSIMINO M R, MAUGERI M. Numerical modelling of centrifuge tests on tunnel-soil systems[J]. Bulletin of Earthquake Engineering, 2014,13(7): 1-25.

[10] LEE J H, KIM J K, KIM J H. Nonlinear analysis of soil-structure interaction using perfectly matched discrete layers[J]. Computers & Structures, 2014, 142: 28-44.

[11] 張巍, 陳清軍. 土-樁-結構非線性相互作用體系行波效應的并行計算分析[J]. 湖南大學學報(自然科學版), 2012, 39(6): 19-25. ZHANG Wei, CHEN Qingjun. Parallel computing analysis of the traveling wave effect of soil-pile-structure nonlinear interaction system finite element analysis of three-dimensional soil-structure interactionsystem[J]. Journal of Hunan University(Natural Sciences),2012, 39(6): 19-25.

[12] LI P, SONG E. Three-dimensional numerical analysis for the longitudinal seismic response of tunnels under an asynchronous wave input[J]. Computers and Geotechnics, 2015, 63: 229-243.

[13] DING J H, JIN X L, GUO Y Z, et al. Numerical simulation for large-scale seismic response analysis of immersed tunnel[J]. Engineering Structures, 2006, 28(10): 1367-1377.

[14] KRYSL P, BITTNAR Z. Parallel explicit finite element solid dynamics with domain decomposition and message passing: dual partitioning scalability[J]. Computers & Structures, 2001, 79(3): 345-360.

[15] FARHAT C. A simple and efficient automatic FEM domain decomposer[J]. Computers & Structures, 1988, 28(5): 579-602.

[16] KARYPIS G, KUMAR V. A fast and high quality multilevel scheme for partitioning irregular graphs[J]. SIAM Journal on Scientific Computing, 1998, 20(1): 359-392.

A study on parallel computing methods for dynamic response analysis of soil-structurenonlinear interaction systems

WANG Xiaoqing1,2, JIN Xianlong1,2, WANG Jianwei2

(1. State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University，Shanghai 200240, China; 2. School of Mechanical Engineering, Shanghai Jiao Tong University，Shanghai 200240, China)

In order to solve the problem of massive amount of computation brought by the numerical dynamic response simulation of soil-structure nonlinear interaction (SSI) systems, a parallel computing method using SSI load balanced and dual-graph theory based domain decomposition (DD) algorithm was proposed. Combined with the traditional greedy and recursive coordinate bisection algorithm, the parallel performance of four algorithms was investigated. The SSI was dealt with the symmetric penalty method. The system equation was solved using the finite element method (FEM) with an explicit central difference scheme. The dynamic responses of typical engineering problems with SSI were simulated in parallel, and the scalability of the four algorithms was analyzed. The results indicate that the SSI load balanced algorithm which substantially balances the coupling loads of soil and structure shows the best parallel efficiency, followed by the dual-graph theory based algorithm and the recursive coordinate bisection algorithm. The greedy method has the lowest parallel efficiency. The parallel efficiency decreases with the number of cores, and the number of cores should be chosen properly according to the scale of the actual model to achieve the optimal parallel performance. The explicit FEM with the penalty method is a proper approach for SSI dynamic analysis.

soil-structure nonlinear interaction; domain decomposition; parallel computing; dynamic response; explicit FEM; symmetric penalty method

國家863高技術研究發展計劃(2012AA01AA307)；國家自然科學基金資助項目(11272214;51475287)

2015-08-11 修改稿收到日期：2015-12-08

王小慶 男，博士生，1988年生

金先龍 男，教授，1961年生

TB122

A

10.13465/j.cnki.jvs.2016.24.004