基于矢量圖的力狀態映射法辨識參數誤差分析

蔣國慶， 李家文, 唐國金

(國防科學技術大學 航天科學與工程學院，長沙 410073)

基于矢量圖的力狀態映射法辨識參數誤差分析

蔣國慶， 李家文, 唐國金

(國防科學技術大學 航天科學與工程學院，長沙 410073)

力狀態映射法被常用于辨識非線性連接結構的等效動力學參數，該方法需要用到實驗儀器測量得到或者經過微分或積分計算得到的激勵力、速度、位移、加速度等數據。而往往這些數據的相位會出現失真，這會直接導致通過力狀態映射辨識得到的系統參數出現誤差。用矢量圖法計算得到了單自由度系統在強迫振動和自由振動兩種情況下出現測量數據或計算數據小幅度相位失真時的誤差計算公式，結果表明這種小幅度相位失真對系統阻尼系數的影響明顯大于對系統剛度系數的影響，且當激勵力頻率等于固有頻率時辨識參數的誤差最小。

矢量圖；力狀態映射法；參數辨識；誤差分析

現代航天器大量使用連接結構，這些連接結構是系統非線性和無源被動阻尼的主要來源之一，連接結構線性模型常常不能反映其非線性特性，必須采用非線性模型，而非線性模型的參數辨識問題是必須解決的關鍵問題之一，一直以來都是學者們的研究熱點[1]。

力狀態映射法是一種用于辨識非線性結構的常用方法，該方法將連接結構的回復力表示為速度和位移的函數，能夠直接顯示系統的剛度特性和阻尼特性。該方法最初由MARSI等[2-3]提出，并經CRAWLEY等[4-5]加以發展和利用。AL-HADID等[6]選用一般多項式對多自由度集總系統進行了辨識，發現一般多項式與正交多項式相比具有物理意義明確的優點。蔡力鋼等[7]采用Tikhonov正則化方法和迭代算法對非線性結合部等效力學模型參數進行了辨識，辨識精度高。吳爽等[8]采用力狀態映射法對太陽翼板間鉸鏈結構非線性動力學模型進行了參數辨識，實驗測試結果和數值仿真結果取得了較好的一致性。

力狀態映射法是一種時域內的方法，需要通過實驗測量得到必要的數據，然而，由于實驗儀器沒有校準或者對實驗數據進行積分或微分處理不恰當會導致各檢測量的相位出現失真，從而導致通過力狀態映射法辨識得到的系統參數出現誤差。WRIGHT等[9]獲得了用力狀態映射法辨識得到的正弦激勵載荷作用下線性系統參數的誤差計算表達式。MESKELL等[10]采用矢量圖法分別建立了單自由度系統在強迫振動和自由振動兩種情況下的模型，分析了激勵力、位移或者速度中某一項發生相位偏差時系統剛度參數和阻尼參數的誤差。但在實際情況下，可能是某兩項的相位發生偏差。本文采用矢量圖法推導得到了單自由度系統在強迫振動和自由振動兩種情況下某兩項發生相位偏差時辨識得到的系統參數誤差公式，誤差公式可以退化至Meskell和Fitzpatrick得到的公式。

1 強迫振動系統參數誤差分析

圖1為單自由度系統強迫振動示意圖，其中F為強迫激勵，其表達式為F=fsin(ωt)，m為質量塊的質量，k為彈簧剛度，c為阻尼系數。系統振動微分方程為

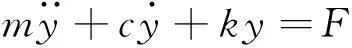
(1)

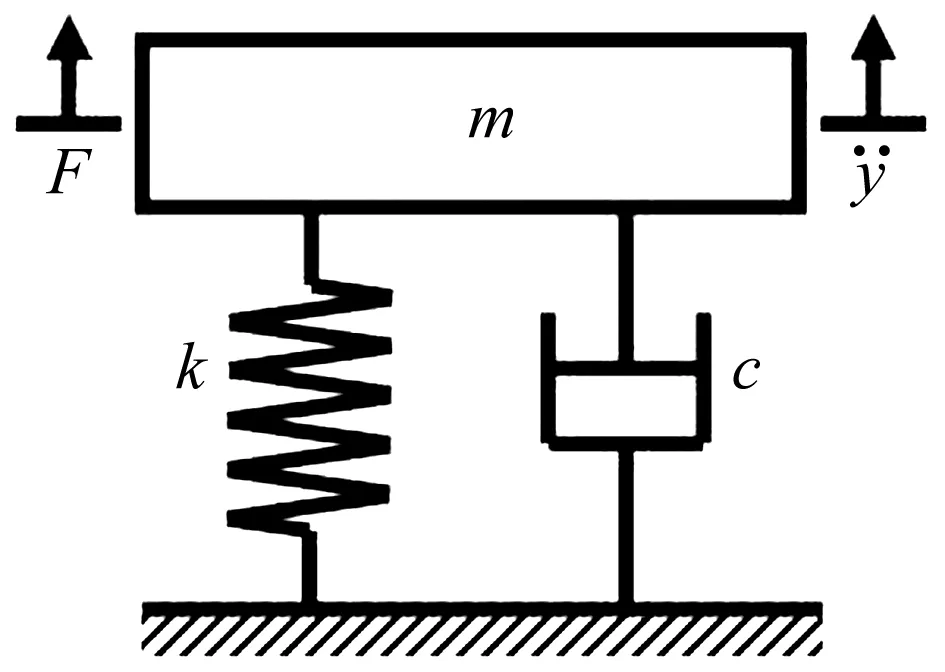
圖1 單自由度系統強迫振動示意圖Fig.1 Schematic of a linear single degree of freedom system

設y0=Asin(ωt-θ)為式(1)的特解，經過換算可以將式(1)變為

(-mω2+jcω+k)ejωt=fejθejωt

(2)

k=fcosθ+mω2

(3)

c=fsinθ

(4)

mω2=kr2

(5)

由式(3)和(5)可以得到

f=(1-r2)k/cosθ

(6)

如果由于試驗時測量設備之間相位沒有校準等原因造成測量或者計算得到的各力的相位出現一定的失真，那么通過力狀態映射法辨識得到的剛度系數和阻尼系數便會出現誤差。文獻[10]中已經利用矢量圖法計算得到了某一項的相位出現偏差時系統剛度系數和阻尼系數的誤差，但實際情況下不能確定發生相位偏差的力的個數，而可能是測量得到的激勵力、速度和位移兩兩出現相位偏差，分別如圖2(b)～(d)所示。當測量得到的三個力均出現相位偏差時，可以通過數據處理(如把所有的相位偏差均減去最小的相位偏差)使得其轉換為兩力出現相位偏差時的情況。

圖2 單自由度強迫振動系統矢量圖Fig.2 Vector diagrams of a linear signal degree of freedom system for forced response

圖2(b)為振動系統測量得到的激勵力和位移的相位均出現偏差時的矢量圖，其中激勵力相位偏差為τ，位移相位偏差為γ，kt和ct為中間剛度系數和阻尼系數，k′和c′為辨識得到的剛度系數和阻尼系數。

由ΔOAB和ΔOCD，可以得到

kt=k+fcos(θ-τ)-fcos(θ)

(7)

ct=fsin(θ-τ)

(8)

由ΔOEF，可以得到

k′=kt/cosγ

(9)

c′=ct+kttanγ

(10)

在此，定義參數誤差比

εk=(k′-k)/k

(11)

εc=(c′-c)/c

(12)

由式(6)、(7)、(9)和(11)可得

(13)

若γ=0，則

εk=(1-r2)(cosτ-1)+2ζrsinτ

(14)

若τ=0，則

(15)

將式(4)、(6)、(8)、(10)和(12)可以得到

εc=(cosτ-1)-((1-r2)/2ζr)sinτ+

(r/2ζ+sinτ+((1-r2)/2ζr)cosτ)tanγ

(16)

若γ=0，則

εc=(cosτ-1)-sinτ(1-r2)/2ζr

(17)

若τ=0，則

εc=tanγ/2ζr

(18)

式(14)、(15)、(17)(18)與文獻[10]中的結果一致。

同理可以得到其余兩種情況下系統剛度系數和阻尼系數的誤差公式，如表1所示。

表1 強迫振動系統剛度系數和阻尼系數誤差Tab.1 Stiffness errors and damper errors of signal degree of freedom for forced response

2 自由振動系統參數誤差分析

圖1中激勵力F=0時該系統即為自由振動系統，其振動微分方程為

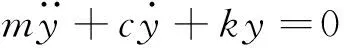
(19)

經過推導可以得到如下式子

(20)

從而有

(21)

根據式(21)可以得到圖3(a)所示矢量圖。

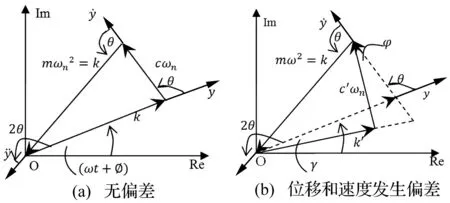
圖3 單自由度自由振動系統矢量圖Fig.3 Vector diagrams of a linear signal degree of freedom system for free response

3 算例分析

對于圖1中的強迫振動系統，取ζ=0.2，τ,γ的變化范圍均為[-4°,4°]，r分別取0.5、1、2，調用MATLAB對式(13)和(16)分別進行計算，計算結果如圖4～圖6所示。

表2 自由振動系統剛度系數和阻尼系數誤差Tab.2 Stiffness errors and damper errors of signal degree of freedom for free response

對圖4～圖6中的計算結果(r=2)統計見表3。

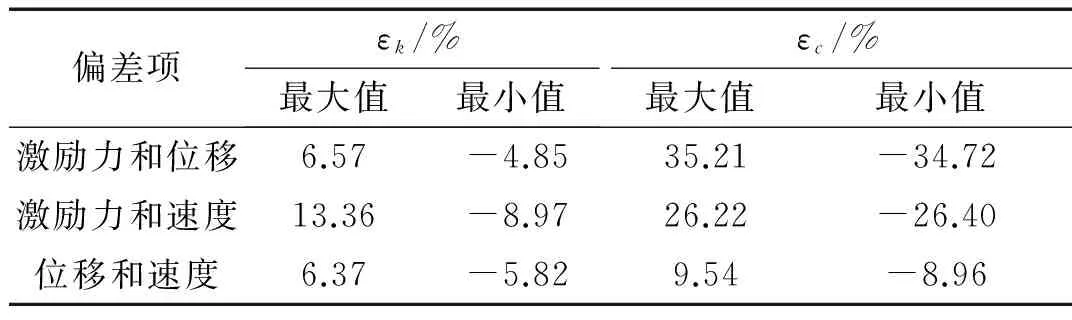
表3 圖4～圖6計算結果統計表Tab.3 Data from Fig.4 to Fig.6(r=2)

由圖4～圖6及表3可知：

(1)激勵力、位移和速度中任意兩項同時發生相位偏差會導致通過力狀態映射法辨識得到的系統剛度系數和阻尼系數出現一定誤差，誤差與激勵力、位移或者速度均為近似線性關系，且這種偏差對系統剛度系數的影響明顯小于對系統阻尼系數的影響；

(2)激勵力和速度相位偏差對剛度系數誤差的影響相近，均大于位移相位偏差對剛度系數誤差的影響；激勵力相位偏差對阻尼系數誤差的影響明顯大于其余兩者的影響；

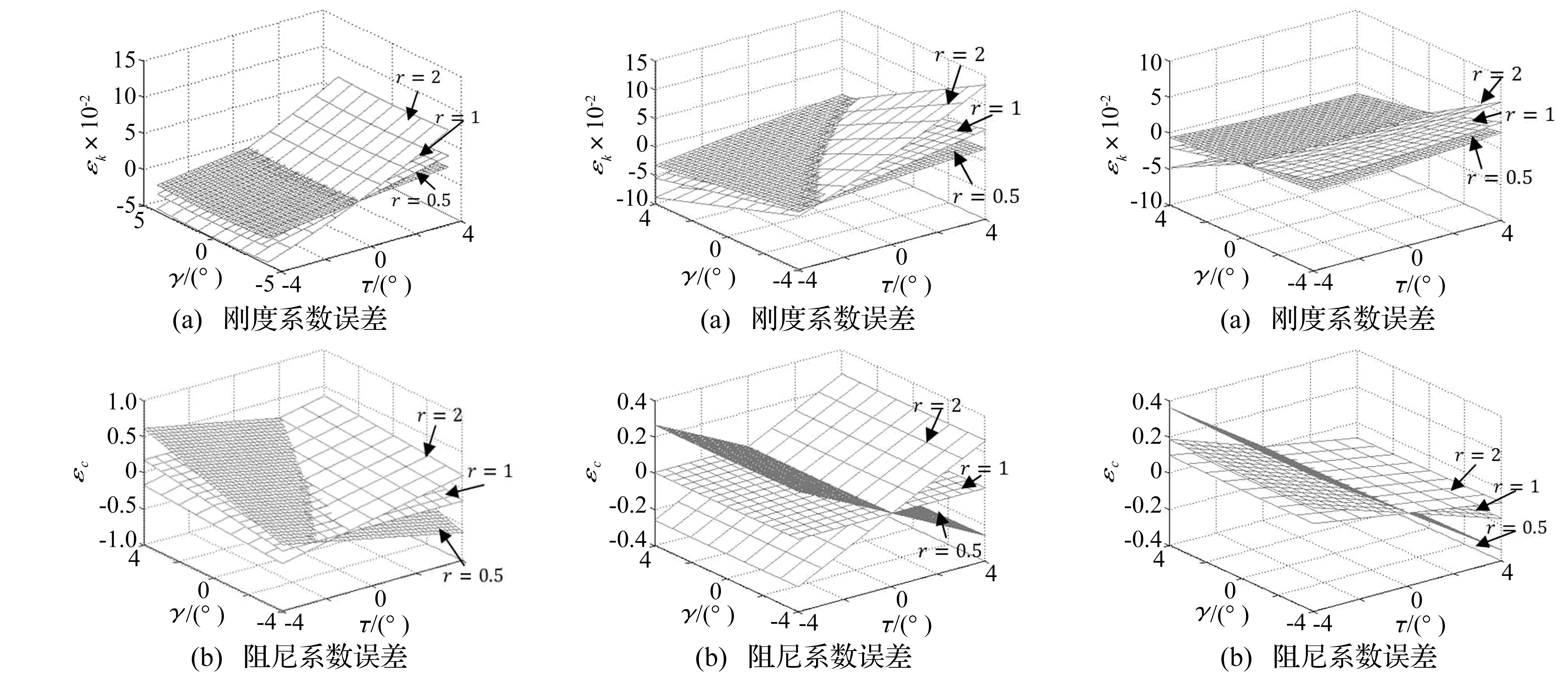
圖4 激勵力和位移相位出現偏差時估計參數誤差Fig.4Parametererrorwhenphasedistortionhappenedonexcitationforceanddisplacement圖5 激勵力和速度相位出現偏差時估計參數誤差Fig.5Parametererrorwhenphasedistortionhappenedonexcitationforceandvelocity圖6 位移和速度相位出現偏差時估計參數誤差Fig.6Parametererrorwhenphasedistortionhappenedondisplacementandvelocity

(3)當激勵力頻率大于固有頻率時，剛度系數和阻尼系數誤差均隨激勵力頻率與固有頻率的比值的增加而增大；當激勵力頻率小于固有頻率時，剛度系數和阻尼系數誤差均隨激勵力頻率與固有頻率比值的較小而增大；當激勵力頻率等于固有頻率時，剛度系數和阻尼系數誤差最小。

4 結 論

本文構造了單自由度系統在強迫振動和自由振動兩種情況下的矢量圖模型，并推導得到了這兩種情況下系統某兩個檢測量出現相位偏差時系統辨識參數的誤差，當退化至某一檢測量發生相位偏差時誤差公式與文獻中對應結果一致。

研究結果表明：

(1)若干檢測量的相位偏差會導致系統辨識參數出現誤差，其中系統剛度系數受到的影響要明顯小于系統阻尼系數受到的影響；

(2)當激勵力頻率等于固有頻率時，辨識參數的誤差最小。

目前矢量圖法只適用于單自由度系統，對于多自由度系統，需要開展進一步研究。

[1] 吳志剛,王本利,馬興瑞.在軌航天器連接結構動力學及其參數辨識[J].宇航學報,1998,19(3):103-109. WU Zhigang, WANG Benli, MA Xingrui. Dynamic and parameters identification of joints in spacecraft [J]. Journal of Astronautics,1998,19(3):103-109.

[2] MARSI S F, CAUGHEY T K. Anon-parametric identification technique for nonlinear dynamic problems [J]. Journal of Applied Mechanics, 1979, 46: 433-447.

[3] MARSI S F, SASSI H, CAUGHEY T K. Nonparametric identification of nearly arbitrary nonlinear systems[J]. Journal of AppliedMechanics, 1982, 49:619-627.

[4] CRAWLEY E F, O’DONNELL K J. Force-state mapping identification of nonlinear joint[J]. AIAA Journal, 1987,25:1003-1010.

[5] CRAWLEY E F, AUBERT A C. Identification of nonlinear structural elements by force-statemapping [J]. AIAA Journal, 1986, 24:155-162.

[6] Al-HADID M A, WRIGHT J R. Developments in the force-state mapping technique for nonlinear systems and the extension to the location of nonlinear elements in a lumpe-parameter system [J]. Mechanical Systems and Signal Processing, 1989 ,3(3):269-290.

[7] 蔡力鋼,李玲,郭鐵能,等.基于力狀態映射法辨識非線性結合部動態參數[J].機械工程學報,2011,47(7):65-72. CAI Ligang, LI Ling, GUO Tieneng, et al. Identification of nonlinear joint parameters with force-state mapping method [J]. Journal of Mechanical Engineering, 2011, 47(7):65-72.

[8] 吳爽,趙壽根,吳大方,等.太陽翼鉸鏈結構的動力學試驗與非線性動力學建模[J].宇航學報,2013,34(12):1550-1556. WU Shuang, ZHAO Shougen, WU Dafang, et al. Dynamic experiments and nonlinear dynamics modeling of joints in solar array [J]. Journal of Astronautics, 2013,34(12):1550-1556.

[9] WRIGHT J R, Al-HADID M A. Sensitivity of the force-state mapping approach to measurement errors [J]. International Journal of Analytical and Experimental Modal Analysis, 1991, 6: 89-103.

[10] MESKELL C, FITZPATRICK J A. Errors in parameter estimates from the force-state mapping technique for free response due to phase distortion [J]. Journal of Sound and Vibration, 2002,252(5):967-974.

Error analysis in parameters from the force-state mapping method based on the vector diagram

JIANG Guoqing，LI Jiawen, TANG Guojin

(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)

The force-state mapping is usually used to identify the equivalent dynamic parameters of a nonlinear joint, which needs lots of data from instruments or from differential or integral, such as excitation force, velocity, displacement, and acceleration. If those signals happen to suffer phase distortion, parameters identified from the force-state mapping will carry errors. Error formulations of identified parameters were derived by the vector diagram when the single degree of freedom system suffered a narrow range of phase distortion. The results indicate that the system stiffness is influenced heavily by the narrow range of phase distortion compared with the system damping.

vector diagram; force-state mapping; parameter identification; error analysis

國家自然科學基金(11502290)；工業裝備結構分析國家重點實驗室項目(GZ15104)

2015-06-29 修改稿收到日期：2015-11-20

蔣國慶 男，博士生，1987年8月生

李家文 男，博士，講師，1982年8月生

O327

A

10.13465/j.cnki.jvs.2016.24.021